本文主要是介绍7.8 dfs竞赛题----素数环(算法竞赛入门经典),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

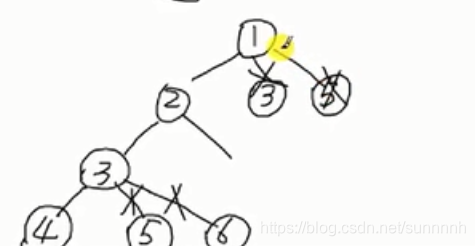
例如:对于序列1 4 3 2 5 6

使用深搜,提前将不符合要求的排序剪枝
伪代码
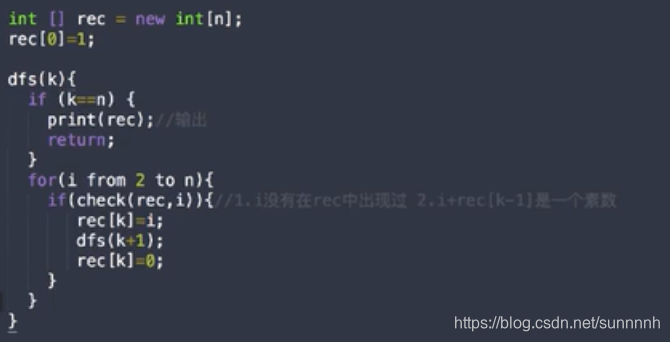
代码:
import java.util.Scanner;public class Main {/**思路:*(1) 首先设置数组res,记录合法的序列,res[0]=1*(2) 从dfs(k)开始深搜,(从k=0开始,k表示当前res中需确定元素的下标位置)*(3)dfs(k) * (3.1)针对当前的k,依次对比1~n的所有数j,通过check()判断是否合法,* (3.1.1)如果合法,则res[k]=j,继续下一个位置的确定,dfs(k+1);* (3.1.2)合法:1.res[k]+res[k-1]为素数* 2.j没有在res出现过* (3.2)出口:当前的k==n**/static int[] res;//记录合法的序列static int n;//n个整数public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();res = new int[n];res[0]=1; //序列从1开始dfs(1);//从下标1位置开始深搜,确定相应下标的元素。注意:一定要从下标1位置开始深搜!下标0位置已经确定}private static void dfs(int k) {//1.如果已确定所有位置,则输出if(k==n && isSu(res[0]+res[n-1])) { //且最后一个元素+第一个元素为素数for(int i=0;i<n;i++) {System.out.print(res[i]+" ");}System.out.println();return;}//2.寻找合法的数字,填入res[k]for(int i=2;i<=n;i++) {//注意:第一个位置已确定为1if(check(k,i)) {res[k]=i;dfs(k+1);res[k]=0;//回溯}}}//判断在res[k]处填元素t是否合法private static boolean check(int k, int t) {//1.判断t是否在res中出现过 以及是否和前面元素相加为素数for(int i=0;i<n;i++) {if(res[i]==t || !isSu(res[k-1]+t)) return false;}return true;}//判断数num是否是素数private static boolean isSu(int num) {for(int i=2;i*i<=num;i++) {if(num%i==0) {return false;}}return true;}}
这篇关于7.8 dfs竞赛题----素数环(算法竞赛入门经典)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






