（推荐）彻底理解ROC曲线和AUC值

本文主要是介绍（推荐）彻底理解ROC曲线和AUC值，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文转自：https://mp.weixin.qq.com/s/a-SL1peqyw9eKyjzFthvlA
二分类模型预测的结果是否足够好，ROC和AUC是重要指标。

1. T、F、P、N、R

首先我们先了解这四个概念：

T：True，真的

F：False，假的

P：Positive，阳性

N：Negative，阴性

R：Rate，比率，和上面四个没直接关系

比如说看病这个事情：

一个人得病了，但医生检查结果说他没病，那么他是假没病，也叫假阴性(FN)

一个人得病了，医生检查结果也说他有病，那么他是真有病，也叫真阳性(TP)

一个人没得病，医生检查结果却说他有病，那么他是假有病，也叫假阳性(FP)

一个人没得病，医生检查结果也说他没病，那么他是真没病，也叫真阴性(TN)

这四种结局可以画成2 × 2的混淆矩阵：

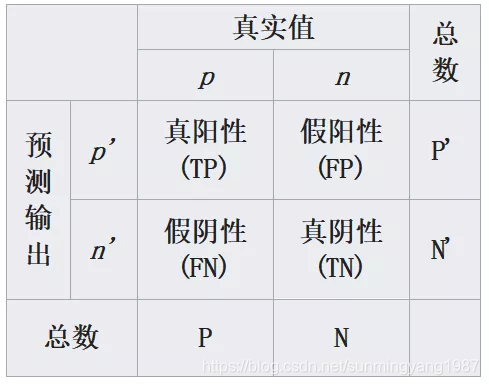
FN、TP、FP、TN可以这样理解：第二个字母(N或P)是医生说的，第一个字母（T或F）是对医生说法的肯定（真没病真阴TN，真有病真阳TP）或否定（假有病假阳FP，假没病假阴FN）。

2. 查出率TPR和查错率FPR

R是Rate(比率)，那么：

TPR，真阳率等于真阳数量除以真阳加假阴，就是真的有病并且医生判断也有病的病人数量除以全部真有病的人（真有病医生也说有病的真阳+真有病医生却说没病的假阴）：

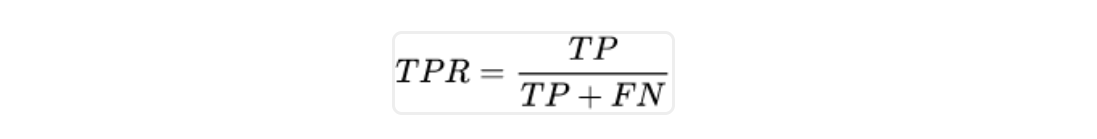
FPR，假阳率等于假阳数量除以假阳加真阴，就是没病但医生说有病的病人数量除以全部实际没病的人（没病但医生说有病的+没病医生也说没病的）：

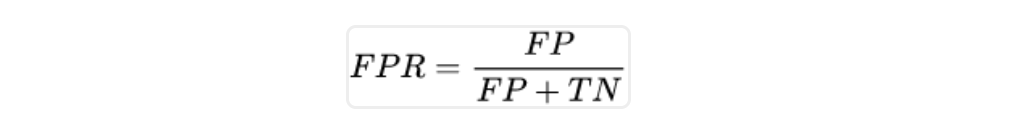
所以说，TPR真阳率是对有病的人的查出率，有病的人里面查出来多少个；而FPR假阳率则是对没病人员的误检率，没病的人里面误检了多少个。
ACC，Accuracy，精准度，有病被检查出来的TP是检测对了，没病也检测健康的TN也是检测对了，所有检测对的数量除以全部数量就是精准度：

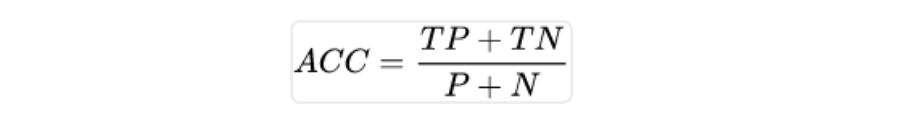
3. 案例计算

假如说我们编写了一个算法M，它能够根据一系列的属性（比如身高、爱好、衣着、饮食习惯等）来预测一个人的性别是男还是女。

然后我们有10个人属性组数据让算法M来预测，这10个人的真实性别和预测结果如下：

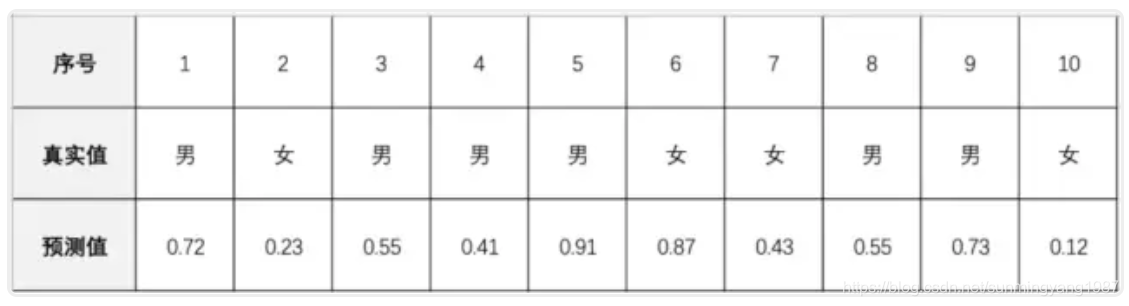
预测值中0代表女性，1代表男性，数字越大越接近男性特征，数字越小越接近女性特征。如果我们设定区分男女的阈值是0.5，那么预测值大于0.5的都是P正向男性，小于0.5都是N负向女性。

那么，真实6个男人中有[1,3,5,8,9]这5个都查出来了，算法M的查出率TPR=5/6=0.833；真实4个女性中6号被查错，所以误检率FPR=1/4=0.25；精度是ACC=(5+3)/10=0.8。

但是注意，如果我们修改阈值等于0.4，那么就会变为6个男人全被检出TPR=1；而女性则被误检2个FPR=0.5；精度仍然是0.8。

4. 随机算法

假设我们有一个庸医，根本不懂医术，当病人来检查是否有病的时候，他就随机乱写有病或者没病，结果呢，对于所有真实有病的，庸医也能正确检查出一半，就是TPR=0.5，同样对于没病的也是一半被误检，就是FPR=0.5。

这个庸医的“随机诊法”原理上总能得到相等的查出率和误检率，如果我们把FPR当做坐标横轴，TPR当做数轴，那么“随机诊法”对应了[0,0]到[1,1]的那条直线。

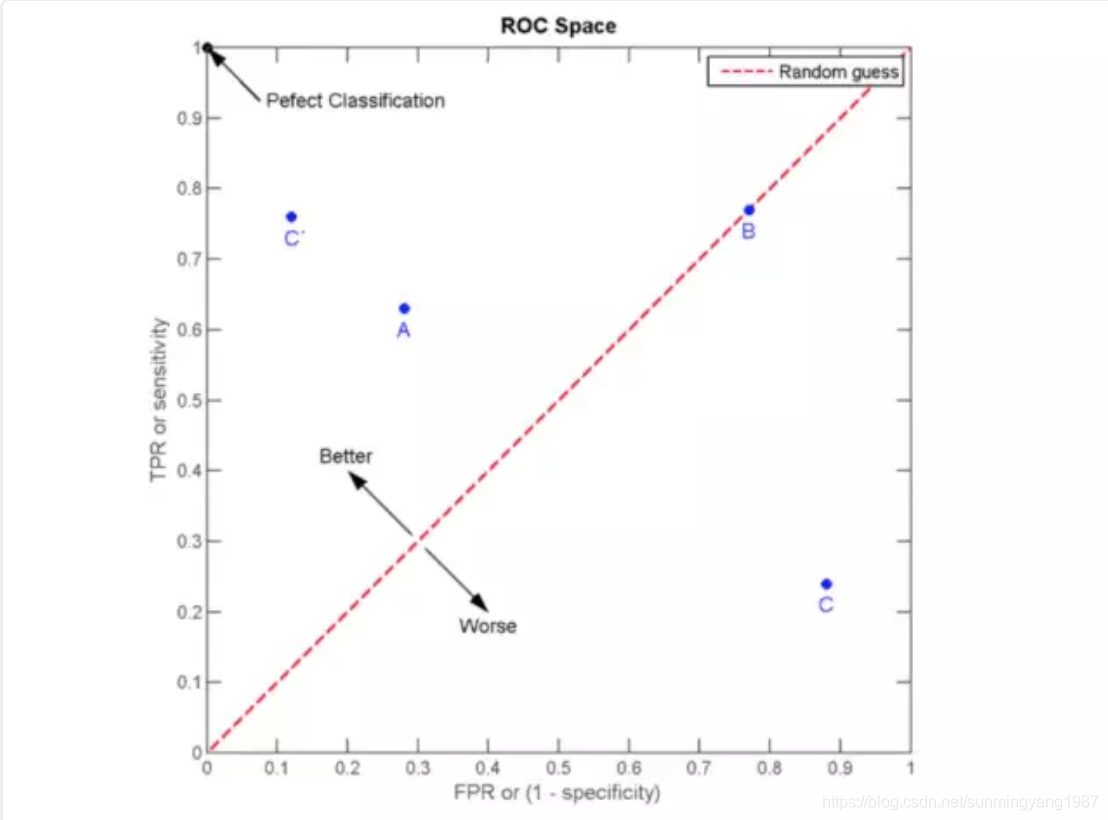
如图所示，越靠近左上角的情况查出率越高，查错率越低，[0,1]点是最完美的状态。而越靠近右下角，算法质量越低。

注意图中右下角C点，这里查错率高，查出率低，属于很糟糕的情况；但是如果我们把C点沿红色斜线对称上去成为C’点，那就很好了。——所以，如果你的算法预测结果总是差的要死，那么可以试试看把它颠倒一下，负负得正，也许就很好了。

5. ROC曲线

ROC(Receiver Operating Characteristic curve)接受者操作特征曲线。

上面我们都只是把从一组预测样本得到的[FPR,TPR]作为一个点描述，并且我们知道阈值的改变会严重影响FPR和TPR，那么，如果我们把所有可能的阈值都尝试一遍，再把样本集预测结果计算得到的所有[FPR,TPR]点都画在坐标上，就会得到一个曲线：

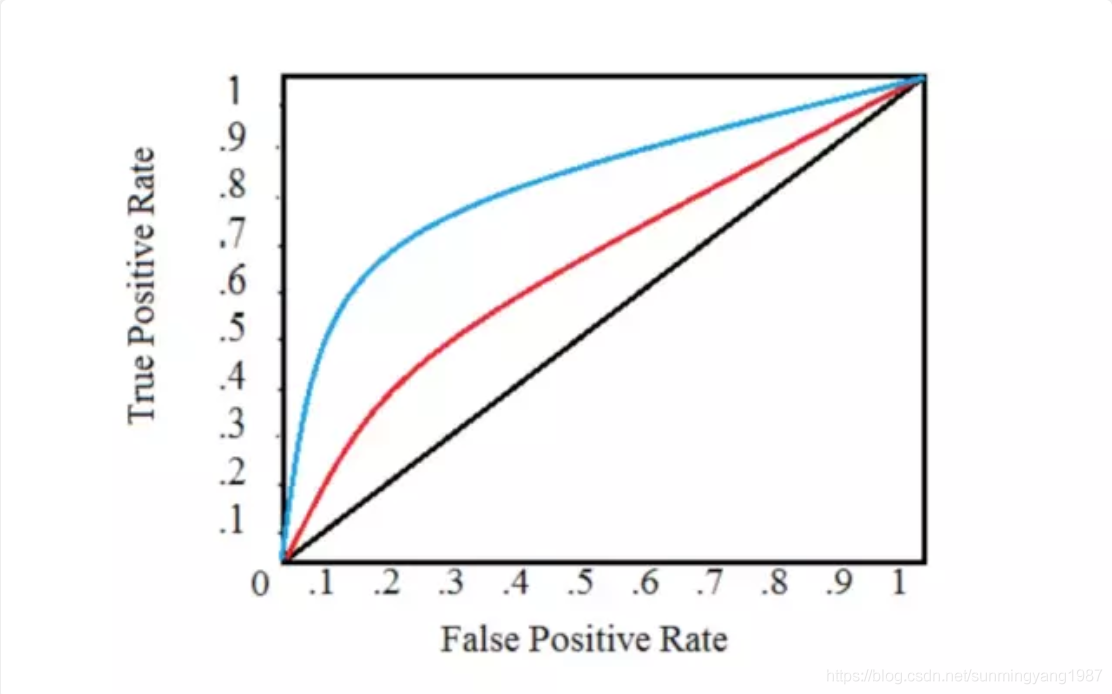
一般阈值范围是在0~1之间，1表示一个分类（男，或者有病），0表示另外一个分类（女，或者无病）。

在这个图中，注意：

横竖都不是阈值坐标轴，这里没有显示阈值。

蓝色线更加靠近左上角，比红色线更好。

ROC曲线上左侧的点好解释，误查率FPR越低，查出率TRP越高，自然是好的；但右上角的怎么解释？误查率和查出率都很高。——想象一下，有个庸医把阈值调的很高比如0.99，那么导致算法推测出来的都是男生，没有女生，这样的情况当然查出率很高（所有男生都查出来了），误查率也很高（所有女生都被当成男生了）。

6. AUC

ROC曲线的形状不太好量化比较，于是就有了AUC。

AUC，Area under the Curve of ROC (AUC ROC)，就是ROC曲线下面的面积。如上图，蓝色曲线下面的面积更大，也就是它的AUC更大。

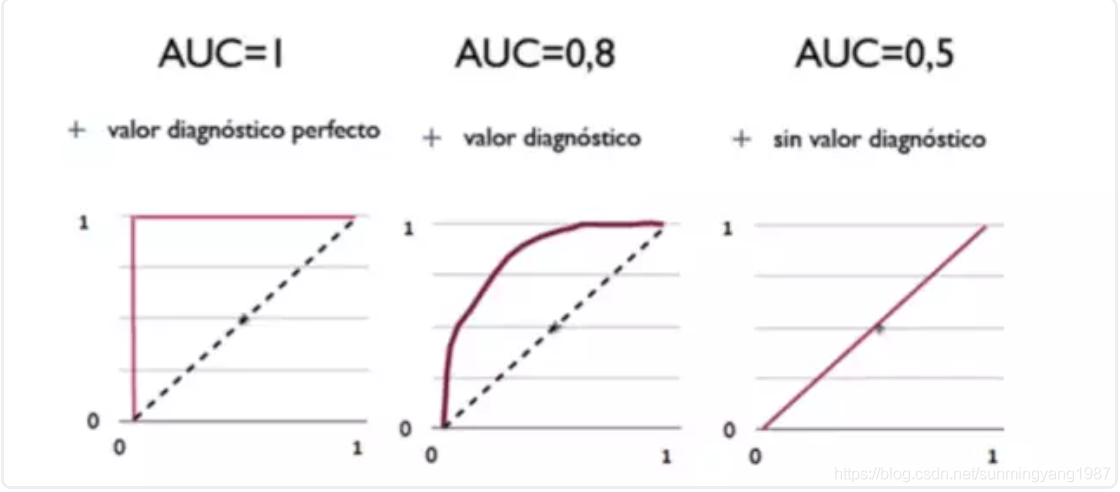
如图，左侧的红色折线覆盖了下面整个方形面积，AUC=1；中间的曲线向左上方凸起，AUC=0.8；右边的是完全随机的结果，占一半面积，AUC=0.5。