黑龙江省赛 Doin‘ Time（区间动态规划）

​​​​​​​​​​​​
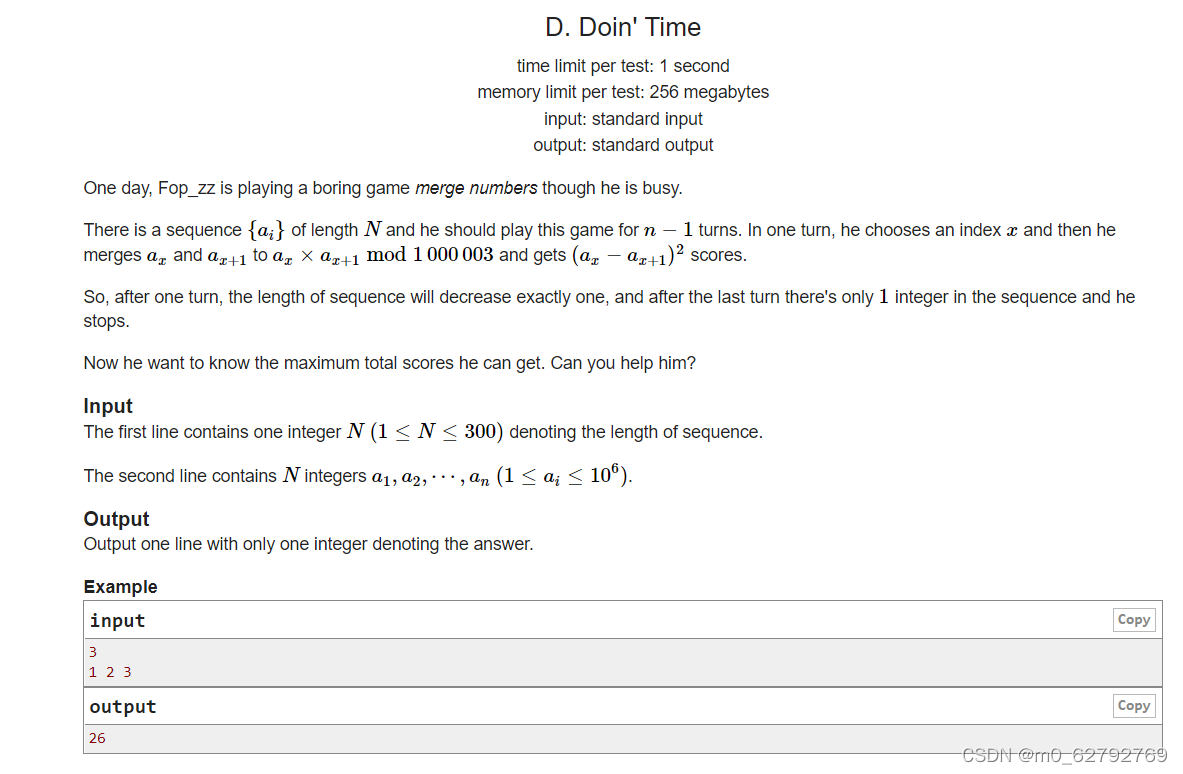
题意： 第一行输入一个数字n，表示数据个数，接下来输入n个数据，你有n - 1 次操作数，每次操作都从其中挑选一对数a[x] 和 a[x + 1] 两个数变成一个数a[x] * a[x + 1],同时产生pow((a[x] - a[x + 1]), 2) 的一个value值，求当最后只剩下一个数字时sumvalue累计的最大值是多少。
**思路：**我们先预处理arry[ i ][ j ] (从i 到 j 位置上所有数乘积的取模)，dp[ l ][ r ] 表示从l到 r 上value 的最大值

转移方程为： dp[l][r] = max(dp[l][r] ,dp[l][k] + dp[k + 1][r] + (arry[l][k] - arry[k + 1][r]) * (arry[l][k] - arry[k + 1][r]))

解释一下转移方程的意思：在[l, r] 的区间内找到最大的sumvalue的值，
首先dp[l][k] 和 d[k + 1][r] 都是已经被处理好的，（在以下的代码中长度从len = 2开始，因此往后所需要的所有子区间的价值都已经是最优的了）因此在每次调用转移方程时都可以看成是最后只剩下两个数变一个数的操作，即都是[l, r]内的最后一步，此时就是前区间的乘积所得到的数和后区间的乘积所得到的数之间进行一步合并取value的操作，最终取sumvalue最大的作为dp[l][r]的值。

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 2e5 + 7;
const int mod = 1e6 + 3;int n, a[305];
LL dp[305][305];
LL arry[305][305];int main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);cin >> n;for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1; i <= n; i++){LL now = 1;for(int j = i; j <= n; j++){now = now * a[j] % mod;arry[i][j] = now;}}for(int len = 2; len <= n; len++){for(int beg = 1; beg + len - 1 <= n; beg++){int l = beg, r= beg + len - 1;for(int k = l; k < r; k++){dp[l][r] = max(dp[l][r] ,dp[l][k] + dp[k + 1][r] + (arry[l][k] - arry[k + 1][r]) * (arry[l][k] - arry[k + 1][r]));}}}cout << dp[1][n] << '\n';
}