数学实验第三版（主编：李继成 赵小艳）课后练习答案（十一）（4）（5）

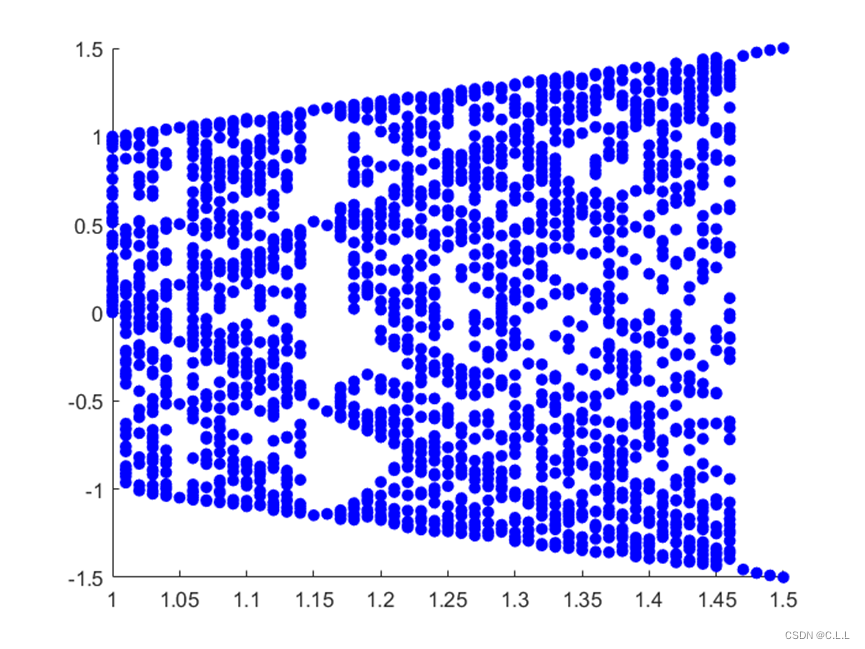
1.费根鲍姆(Feigenbaum)对超越函数  (λ为非负实数)进行了分叉与混沌的研究,试利用迭代格式 ,做出相应的费根鲍姆图.

clc;clear;
a=0.5;%x初值取0.5
for l=1:0.01:1.5hold on
x=[a];
for k=2:150x(k)=l*sin(pi*x(k-1));
end
pause(0.1);
for i=100:150%取后50个点plot(l,x(i),'b.','markersize',20);
end
end

2.令 ,a分别取5,11,15,b>0(任意),初值 =1.参照示例6,观察分叉与混沌现象.

clc;clear;x0=1;%x初值为1
a=[5,11,15];b=5;
for l=1:3hold on
x=[x0];
for k=2:150x(k)=a(l)*x(k-1)*exp(-b*x(k-1));
end
pause(0.1);
for i=100:150%取后50个点plot(a(l),x(i),'b.','markersize',20);
end
end

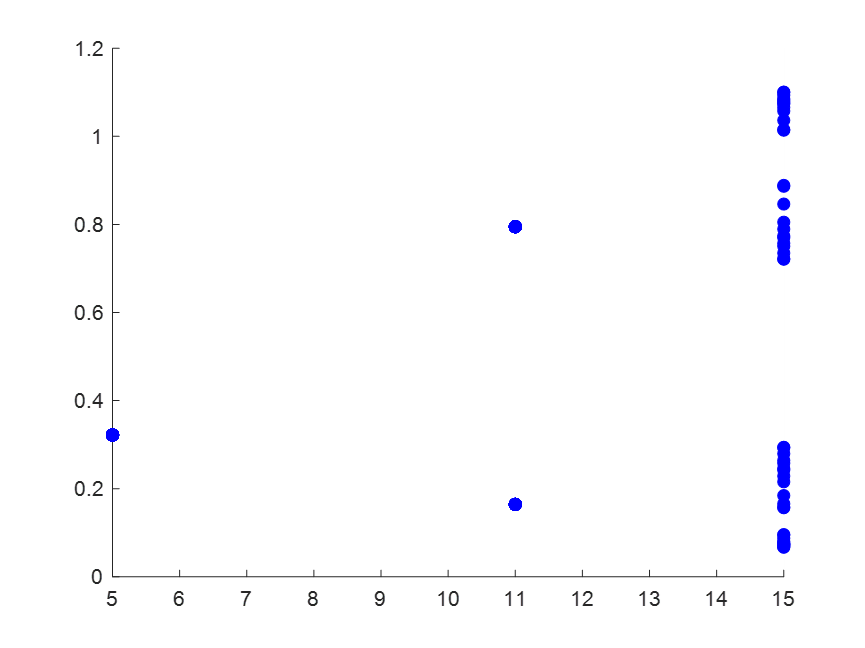
此时我们发现对应不同的a值，迭代后五十次所产生的数由收敛变为了在两个数之间摆动，然后变为了没有规律。

然后我们缩小步长，在[5,15]区间内进行上述实验：

clc;clear;x0=1;%x初值为1
b=5;
for l=5:0.1:15hold on
x=[x0];
for k=2:150x(k)=l*x(k-1)*exp(-b*x(k-1));
end
pause(0.1);
for i=100:150%取后50个点plot(l,x(i),'b.','markersize',20);
end
end

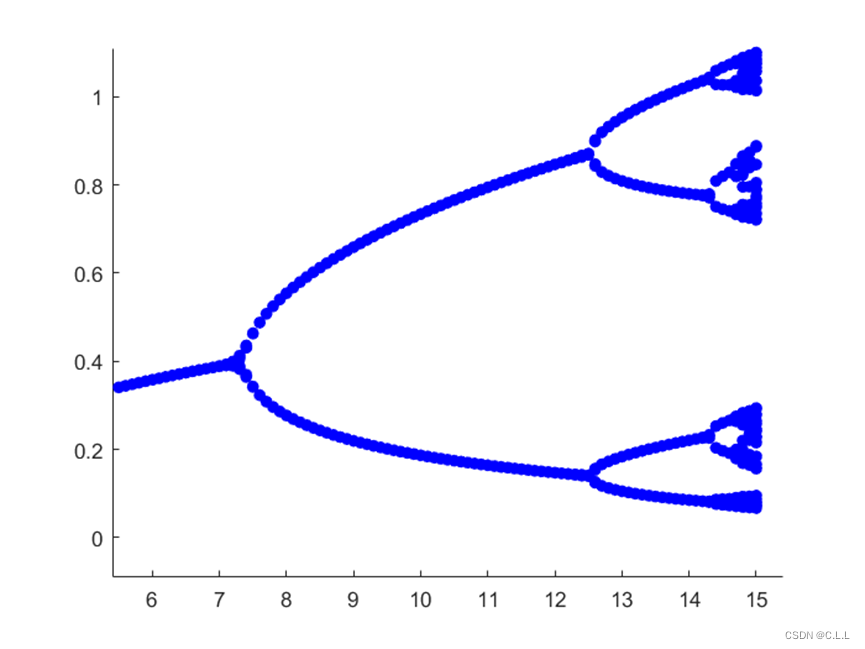
轨道由一支变为了两支进而称为四支、八支等等，出现了倍周期现象。

其次我们再来研究该迭代序列对初值的依赖性：

clc;clear;x0=[1,25,50];
a=5;%取a为5
b=5;
for i=1:3
x=[x0(i)];
for k=2:100x(k)=a*x(k-1)*exp(-b*x(k-1));
end
hold on
plot(1:k,x,'.');
x=[];
end
legend('1','25','50');

经过实验得知，该迭代序列对初始值的依赖型不大。

3.对帐篷映射

先取 ,然后由 开始逐渐慢慢地增加 的值,用数值方法考察由初值 出发的轨道 .能否看到倍周期的分叉现象?

clc;clear;x0=0.2;
for a=[0.3,0.5:0.01:1]
x=[x0];
for k=2:150x(k)=a*(1-2*abs(x(k-1)-1/2));
end
hold on
pause(0.1);
for i=100:150
plot(a,x(i),'r.');
end
end

我们看到了明显的周期分叉现象。

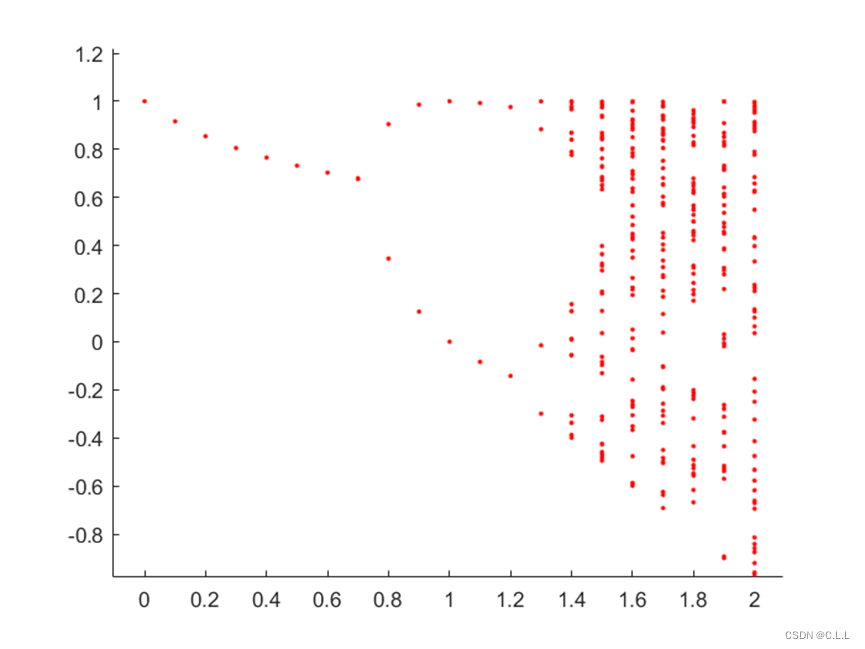
4.作出映射 的分支混沌图。

clc;clear;x0=0.2;
for u=0:0.1:2
x=[x0];
for k=2:150x(k)=1-u*x(k-1)^2;
end
hold on
pause(0.1);
for i=100:150
plot(u,x(i),'r.');
end
end

练习五

1.求下列非线性方程组的解:

（1）  初值为（0,0）；

clc;clear;
[x,y]=fsolve(@fun2,[0,0]) 
function f=fun2(x)
f(1)=x(1)-0.7*sin(x(1))-0.2*cos(x(2));
f(2)=x(2)-0.7*cos(x(1))+0.2*sin(x(2))
end

x =

   0.526522622595098   0.507919719227252

y =

   1.0e-09 *

   0.285771850627725   0.461794200101728

（2） 初值为（a）[1.4,-1.5]; (b) [3.7,2.7]

clc;clear;
[x1,y1]=fsolve(@fun3,[1.4,-1.5])
[x2,y2]=fsolve(@fun3,[3.7,2.7])
function f=fun3(x)
f(1)=2*x(1)^2-x(1)*x(2)-5*x(1)+1;
f(2)=x(1)+3*log10(x(1))-x(2)^2;
end

x1 =

   1.458890230151366  -1.396767009183311

y1 =

   1.0e-11 *

   0.065725203057809  -0.626454443874991

x2 =

   3.487442816247016   2.261628683716998

y2 =

   1.0e-06 *

   0.005903718403033  -0.201181419967611

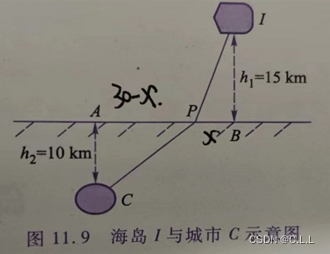
2.为了在海岛1与某城市C之间铺设一条地下光缆,如图11.9所示,每千米光缆铺设成本在水下部分是C1 ,在地下部分是C2 ,为使得铺设光缆的总成本最低,光缆的转折点P(海岸线上)应该取在何处?如果实际测得海岛1与城市C之间水平距离AB=30km,海岛距海岸线h1 =15km,城市距海岸线h2 =10 km, C1 =3000万元/km, C2 =1500万元/km,求P点坐标(误差< km).

clc;clear;
syms x
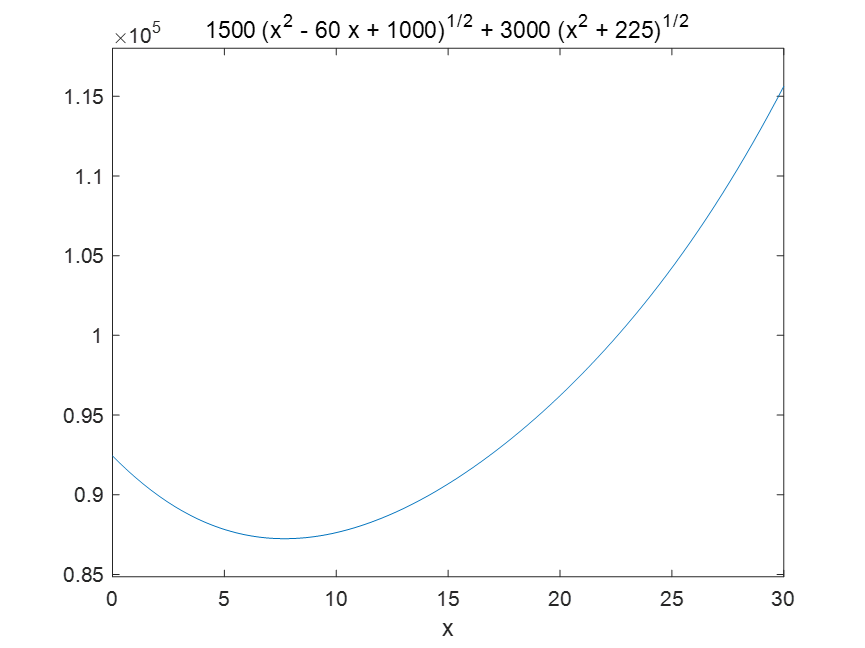
w=3000*sqrt(x^2+15^2)+1500*sqrt((30-x)^2+10^2);
w=expand(w);
ezplot(w,[0,30]);
y='3000*sqrt(x^2+15^2)+1500*sqrt((30-x)^2+10^2)';
[x,min]=fminbnd(y,0,30)

x =7.691078497321983

min = 8.724197430766789e+04

3.有一艘宽为5m的长方形驳船欲驶过某河道的直角湾,经测量知河道的宽度为10m和12m,如图11.10所示.试问,要驶过该直角湾,驳船的长度不能超过多少 m?(误差< m)

见下侧手绘图，我们先要找到拐弯的极限状态，即船身和两侧的河道紧挨在一起。然后我们此时设内侧船身和左侧河岸的夹角为θ，求出船长即可。

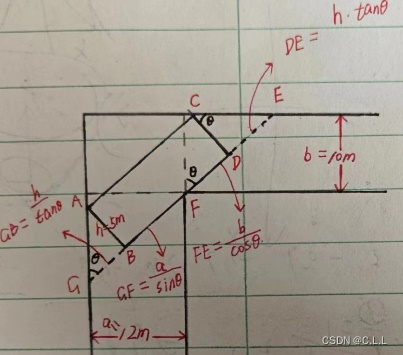
则BD=GE-GB-DE

     =GF+FE-GB-DE

     =a/sinθ+b/cosθ-h/tanθ-h·tanθ；

由于船在转向的时候，θ一直在[0,pi/2]范围内改变，则船长一定要小于这个函数的最小值才可避免过不去的现象。

clc;clear;
a=12;b=10;h=5;
syms t
BD=a/sin(t)+b/cos(t)-h/tan(t)-h*tan(t);
ezplot(BD,[0,pi/2]);
f=matlabFunction(BD);
[x,min]=fminbnd(f,0,pi/2)

x =

    0.8388

min =

   21.0372

则船长不能超过21.0372m。

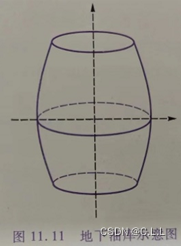
4.一个对称的地下油库,内部设计如图11.11所示:横截面为圆,中心位置处的截面半径为3m,上下底处的半径为2m,高为12m,纵截面的两侧是顶点在中心位置的抛物线

试求:

(1)油库内油面的深度为h(从底部算起)时,库内油量的容积 V(h).

clc;clear;
syms y x h
m=((y^2-108)/36)^2;
v=int(m,y,-6,x);
v=subs(v,x,h-6)

v =

9*h - (h - 6)^3/18 + (h - 6)^5/6480 - 54/5

(2)设计测量油库油量的标尺.即当油量容积V已知时,算出油的深度h,刻出油量大小.试给出当V=10 ,20 ,30 ,…时油的深度.

clc;clear;
format long
syms y x h 
m=((y^2-108)/36)^2;
v=int(m,y,-6,x);
v=subs(v,x,h-6);
v1=[10,20,30];
for i=1:3v2=v1(i);double(solve(v==v2,'Real',1))
end

ans =

   1.907763147608878

ans =

   3.303659306836313

ans =

   4.513168476010395

本文由作者自创，由于时间原因，难免出现些许错误，还请大家多多指正。创作不易，请大家多多支持。