《合成孔径雷达成像算法与实现》Figure6.18

2024-02-16 13:52
文章标签 算法 实现 成像 合成孔径雷达 figure6.18

本文主要是介绍《合成孔径雷达成像算法与实现》Figure6.18，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！ 

% rho_r = c/(2*Fr)而不是rho_r = c/(2*Bw)
% Hsrcf exp函数里忘记乘pi了
clc
clear
close all参数设置
距离向参数设置
R_eta_c = 20e3;             % 景中心斜距
Tr = 2.5e-6;                % 发射脉冲时宽
Kr = 20e12;                 % 距离向调频率
alpha_os_r = 1.2;           % 距离过采样率
Nrg = 320;                  % 距离线采样数
距离向参数计算
Bw = abs(Kr)*Tr;            % 距离信号带宽
Fr = alpha_os_r*Bw;         % 距离向采样率
Nr = round(Fr*Tr);          % 距离采样点数（脉冲序列长度）
方位向参数设置
c = 3e8;                    % 光速
Vr = 150;                   % 等效雷达速度
Vs = Vr;                    % 卫星平台速度
Vg = Vr;                    % 波束扫描速度
f0 = 5.3e9;                 % 雷达工作频率
Delta_f_dop = 80;           % 多普勒带宽
alpha_os_a = 1.25;          % 方位过采样率
Naz = 256;                  % 距离线数
theta_r_c = 21.9;            % 波束斜视角
方位向参数计算
lambda = c/f0;              % 雷达工作波长
eta_c = -R_eta_c*sind(theta_r_c)/Vr;% 波束中心偏移时间
f_eta_c = 2*Vr*sind(theta_r_c)/lambda;% 多普勒中心频率
La = 0.886*2*Vs*cosd(theta_r_c)/Delta_f_dop;% 实际天线长度
Fa = alpha_os_a*Delta_f_dop;% 方位向采样率
Ta = 0.886*lambda*R_eta_c/(La*Vg*cosd(theta_r_c));% 目标照射时间
R0 = R_eta_c*cosd(theta_r_c);% 最短斜距
Ka = 2*Vr^2*cosd(theta_r_c)^3/(lambda*R0);% 方位向调频率
theta_bw = 0.886*lambda/La; % 方位向3dB波束宽度
theta_syn = Vs/Vg*theta_bw; % 合成角
Ls = R_eta_c*theta_syn;     % 合成孔径
其他参数计算
rho_r = c/2/Fr;             % 距离向分辨率 
rho_a = La/2;               % 方位向分辨率
Trg = Nrg/Fr;               % 发射脉冲宽度
Taz = Naz/Fa;               % 目标照射时间
d_t_tau = 1/Fr;             % 距离向采样时间间隔
d_t_eta = 1/Fa;             % 方位向采样时间间隔
d_f_tau = Fr/Nrg;           % 距离向采样频率间隔
d_f_eta = Fa/Naz;           % 方位向采样频率间隔目标设置
设置目标点距离景中心的距离
% A_r = -50;A_a = -50;
% B_r = -50;B_a = +50;
C_r = +50;C_a = +90;
坐标
% A_x = R0+A_r;A_y = A_a;
% B_x = R0+B_r;B_y = B_a;
C_x = R0+C_r;C_y = C_a;
N_position = [%A_x,A_y;B_x,B_y;C_x,C_y];
波束中心穿越时刻
N_target = 1;
Target_eta_c = zeros(1,N_target);
for i = 1:N_targetDelta_Y = N_position(i,2)-N_position(i,1)*tand(theta_r_c);Target_eta_c(i) = Delta_Y/Vs;
end
绝对零多普勒时刻
Target_eta_0 = zeros(1,N_target);
for i = 1:N_targetTarget_eta_0(i) = N_position(i,2)/Vs; 
end变量设置
时间变量：以景中心绝对零多普勒时刻作为方位向零点
t_tau = (-Trg/2:d_t_tau:Trg/2-d_t_tau)+2*R_eta_c/c;     % 距离时间变量
t_eta = (-Taz/2:d_t_eta:Taz/2-d_t_eta)+eta_c;           % 方位时间变量
r_tau = (t_tau*c/2)*cosd(theta_r_c);                    % 最近距离变量
频率变量
f_tau = fftshift(-Fr/2:d_f_tau:Fr/2-d_f_tau);           % 距离频率变量
f_tau = f_tau-round((f_tau-0)/Fr)*Fr;                   % 将频率折叠入(-Fr/2,Fr/2)，距离可观测频率变量
f_eta = fftshift(-Fa/2:d_f_eta:Fa/2-d_f_eta);           % 方位频率变量
f_eta = f_eta-round((f_eta-f_eta_c)/Fa)*Fa;             % 将频率折叠入f_eta_c附近(-Fa/2,Fa/2)范围，方位可观测频率变量
坐标设置
[t_tauX,t_etaY] = meshgrid(t_tau,t_eta);                % 距离时间X轴，方位时间Y轴
[f_tauX,f_etaY] = meshgrid(f_tau,f_eta);                % 距离频域X轴，方位频域Y轴
[r_tauX,f_eta_Y] = meshgrid(r_tau,f_eta);               % 距离长度X轴，方位频域Y轴信号设置，原始回波生成
tic                                                     % 计时，与toc搭配使用
wait_title = waitbar(0,'开始生成回波数据 ...'); 
pause(1);
st_tt = zeros(Naz,Nrg);
for i = 1:N_targetR_eta = sqrt(N_position(i,1)^2+Vs^2*(t_etaY-Target_eta_0(i)).^2);% 瞬时斜距，还有近似公式可以尝试A0 = [1,1,1,1]*exp(+1j*0);                          % 后向散射系数wr = (abs(t_tauX-2*R_eta/c)<=Tr/2);                 % 距离向包络wa = sinc(0.886*atan(Vs*(t_etaY-Target_eta_c(i))/N_position(i,1))/theta_bw).^2;% 方位向包络，用波束穿越时刻
%     wa = sinc(0.886*(atan(Vs*(t_etaY-Target_eta_0(i))/N_position(i,1))+theta_r_c)/theta_bw).^2;st_tt_target = A0(i)*wr.*wa.*exp(-1j*4*pi*f0*R_eta/c)....*exp(1j*pi*Kr*(t_tauX-2*R_eta/c).^2);st_tt = st_tt+st_tt_target;pause(0.001);time = toc;Display_Data = num2str(roundn(i/N_target*100,-1));Display_Str  = ['Computation Progress',Display_Data,'%',' --- ',...'Using Time: ',num2str(time)];waitbar(i/N_target,wait_title,Display_Str);         % 三参数：进度，句柄，展示的话
end
pause(1);
close(wait_title);
tocH = figure();
set(H,'position',[100,100,600,600]);
subplot(221)
imagesc(real(st_tt))
xlabel('距离时间(采样点)'),ylabel('方位时间(采样点)'),title('(a)实部')
subplot(222)
imagesc(imag(st_tt))
xlabel('距离时间(采样点)'),ylabel('方位时间(采样点)'),title('(b)虚部')
subplot(223)
imagesc(abs(st_tt))
xlabel('距离时间(采样点)'),ylabel('方位时间(采样点)'),title('(c)幅度')
subplot(224)
imagesc(angle(st_tt))
xlabel('距离时间(采样点)'),ylabel('方位时间(采样点)'),title('(d)相位')一次距离压缩
方式三：根据脉冲频谱特性直接在频域生成频域匹配滤波器
window = kaiser(Nrg,2.5)';              % 时域窗
Window = fftshift(window);              % 频域窗
% 计算滤波器
Hrf = (abs(f_tauX)<=Bw/2).*Window.*exp(+1j*pi*f_tauX.^2/Kr);
Sf_ft = fft(st_tt,Nrg,2);
Srf_ft = Sf_ft.*Hrf;
srt_tt = ifft(Srf_ft,Nrg,2);figure('Name','一次距离压缩'),subplot(121)
imagesc(real(srt_tt))
xlabel('距离时间(采样点)'),ylabel('方位时间(采样点)'),title('(a)实部')
subplot(122)
imagesc(abs(srt_tt))
xlabel('距离时间(采样点)'),ylabel('方位时间(采样点)'),title('(b)虚部')% 方位向FFT
% Saf_tf = fft(srt_tt,Naz,1);
% 
% figure('Name','方位FFT'),subplot(121)
% imagesc(real(Saf_tf)),set(gca,'YDir','normal')
% xlabel('距离时间(采样点)'),ylabel('方位时间(采样点)'),title('(a)实部')
% subplot(122)
% imagesc(abs(Saf_tf)),set(gca,'YDir','normal')
% xlabel('距离时间(采样点)'),ylabel('方位时间(采样点)'),title('(b)幅度')
二次距离压缩
D0 = sqrt(1-lambda^2*f_eta_c^2/(4*Vr^2));
Kscr = 2*Vr^2*f0^3*D0^3/(c*R0*f_eta_c^2);
Hsrcf = exp(-1j*pi*f_tauX.^2/Kscr);Srf_ff = fft(Srf_ft,Naz,1);
% Srf_tf = ifft(Srf_ff,Nrg,2);
% figure,imagesc(abs(Srf_tf)),title('方位向FFT'),set(gca,'YDir','normal')% S_ff = fft(Saf_tf,Nrg,2);
S_ff_scr = Srf_ff.*Hsrcf;
S_tf_scr = ifft(S_ff_scr,[],2);
s_tt_scr = ifft2(S_ff_scr);figure,imagesc(abs(S_tf_scr)),set(gca,'YDir','normal'),title('SRC')% figure
% subplot(121),imagesc(abs(Srf_tf)),set(gca,'YDir','normal')
% subplot(122),imagesc(abs(S_tf_scr)),set(gca,'YDir','normal')% S_ff_1 = fft(Srf_tf,Naz,1);
% S_ff_scr_1 = S_ff_1.*Hsrcf;
% S_tf_scr = ifft(S_ff_scr_1,[],2);
%  绘图
H5 = figure('Name','二次距离压缩后');
set(H5,'position',[100,100,600,300]); 
subplot(121),imagesc(real(s_tt_scr))
%  axis([0 Naz,0 Nrg])
xlabel('距离时间(采样点)→'),ylabel('←方位时间(采样点)'),title('(a)实部')
subplot(122),imagesc( abs(s_tt_scr))
%  axis([0 Naz,0 Nrg])
xlabel('距离时间(采样点)→'),ylabel('←方位时间(采样点)'),title('(b)幅度')距离徙动校正——8点插值
% RCM = lambda^2*r_tauX.*f_etaY.^2/(8*Vr^2);
% RCM = R0+RCM-R_eta_c;                       % 将距离徙动量转换到原图坐标系下
D = sqrt(1-lambda^2*f_etaY.^2/(4*Vr^2));              % 距离多普勒域中的徙动因子
RCM = r_tauX./D-r_tauX;
RCM = R0+RCM-R_eta_c;                       % 将距离徙动量转换到原图坐标系下
offset = RCM/rho_r;                         % 将距离徙动量转换为距离单元偏移量
计算插值表
x_tmp = repmat(-4:3,[16,1]);                % 插值长度
x_tmp = x_tmp+repmat(((1:16)/16).',[1,8]);   % 量化位移
% figure,imagesc(repmat(((1:16)/16)',[1,8])),colorbar
% figure,imagesc(repmat(-4:3,[16,1])),colorbar
% figure,imagesc(repmat(((1:16)/16)',[1,8])+repmat(-4:3,[16,1])),colorbar
hx = sinc(x_tmp);                           % 生成插值核
% % figure,imagesc(hx)
hx = kaiser(8,2.5)'.*hx;
hx = hx./sum(hx,2);                         % 归一化
插值表校正
Srcmf_tf_8 = zeros(Naz,Nrg);
for a_tmp = 1:Nazfor r_tmp = 1:Nrgoffset_ceil = ceil(offset(a_tmp,r_tmp));offset_frac = round((offset_ceil-offset(a_tmp,r_tmp))*16);if offset_frac == 0Srcmf_tf_8(a_tmp,r_tmp) = S_tf_scr(a_tmp,ceil(mod(r_tmp+offset_ceil-0.1,Nrg)));elseSrcmf_tf_8(a_tmp,r_tmp) = S_tf_scr(a_tmp,ceil(mod((r_tmp+offset_ceil-4:r_tmp+offset_ceil+3)-0.1,Nrg)))*hx(offset_frac,:).';endend
endfigure('Name','8点距离徙动校正'),subplot(121)
imagesc(real(Srcmf_tf_8)),set(gca,'YDir','normal')
xlabel('距离时间(采样点)'),ylabel('方位频率(采样点)'),title('(a)实部')
subplot(122)
imagesc(abs(Srcmf_tf_8)),set(gca,'YDir','normal')
xlabel('距离时间(采样点)'),ylabel('方位频率(采样点)'),title('(b)幅度')方位压缩
Ka = 2*Vr^2*cosd(theta_r_c)^3./(lambda*r_tauX);
Haf = exp(-1j*pi*f_etaY.^2./Ka);                    % 匹配滤波器
Haf_offset = exp(-1j*2*pi*f_etaY*eta_c);            % 时间补偿项
Soutf_tf = Srcmf_tf_8.*Haf.*Haf_offset;
soutt_tt = ifft(Soutf_tf,Naz,1);绘图
H1 = figure();
set(H1,'position',[100,100,600,300]); 
subplot(121),imagesc(real(soutt_tt))
xlabel('距离时间(采样点)→'),ylabel('←方位时间(采样点)'),title('(a)实部')
subplot(122),imagesc( abs(soutt_tt)),colorbar
xlabel('距离时间(采样点)→'),ylabel('←方位时间(采样点)'),title('(b)幅度')点目标分析
len = 16;
cut = -len/2:len/2-1;
% sout_tt_C = soutt_tt(round(Naz/2+1+N_position(3,2)/Vr*Fa)+cut, ...
%                     round(Nrg/2+1+2*(N_position(3,1)-R0)/c*Fr)+cut);
sout_tt_C = soutt_tt(226+cut, 181+cut);
figure,imagesc(abs(sout_tt_C)),title('切片')Sout_ff_C = fft2(sout_tt_C);
figure,imagesc(abs(Sout_ff_C)),set(gca,'YDir','normal')len = 48;
cut = -len/2:len/2-1;
% sout_tt_C = soutt_tt(round(Naz/2+1+N_position(3,2)/Vr*Fa)+cut, ...
%                     round(Nrg/2+1+2*(N_position(3,1)-R0)/c*Fr)+cut);
sout_tt_C_1 = soutt_tt(226+cut, 181+cut);
figure,imagesc(abs(sout_tt_C_1)),title('切片')Sout_ff_C_1 = fft2(sout_tt_C_1);
figure,imagesc(abs(Sout_ff_C_1)),set(gca,'YDir','normal')Start_ff_1 = Sout_ff_C;% 高频补零
Start_buling_1 = zeros(len,16*len);
Start_buling_2 = zeros(16*len,16*len);
% 行补零
for i = 1:len[~,I] = min(Start_ff_1(i,:));Start_buling_1(i,1:I) = Start_ff_1(i,1:I);Start_buling_1(i,16*len-(len-I)+1:16*len) = Start_ff_1(i,I+1:end);
end
% 列补零
for i = 1:16*len[~,I] = min(Start_buling_1(:,i));Start_buling_2(1:I,i) = Start_buling_1(1:I,i);Start_buling_2(16*len-(len-I)+1:16*len,i) = Start_buling_1(I+1:end,i);
endstart_tf_1 = ifft(Start_buling_2,[],2);
start_tt_2 = ifft(start_tf_1,[],1);
% Start_ff_2 = fft2(start_tt_2);
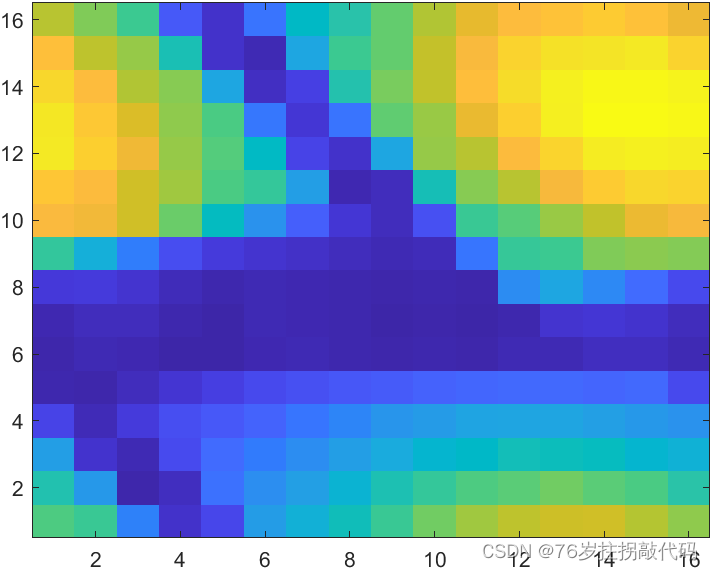
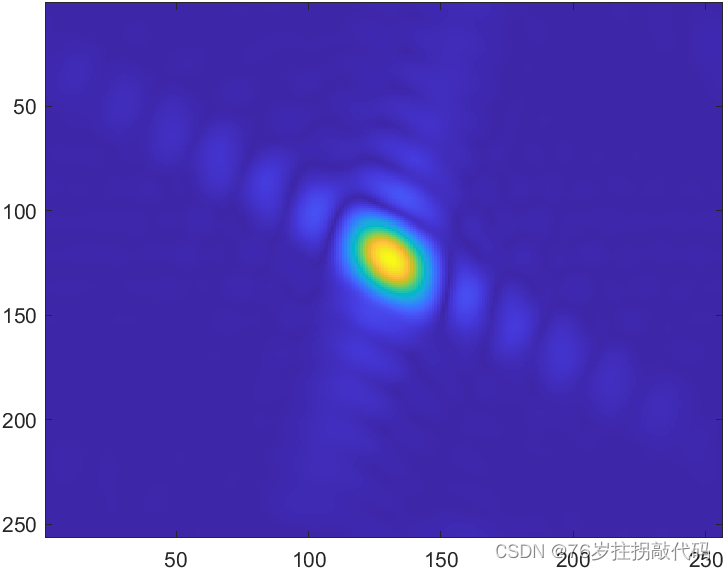
% figure,imagesc(abs(fftshift(Start_ff_2))),set(gca,'YDir','normal')figure('Name','高频补零'),imagesc(abs(start_tt_2))
contour(abs(start_tt_2),15)% p为行索引，q为列索引
[aa,p] = max(start_tt_2);
[bb,q] = max(max(start_tt_2));% 距离切片
start_r = abs(start_tt_2(p(q),:));
start_r = db(start_r/max(start_r));
figure,plot(start_r),ylim([-35,0])% 方位切片
start_a = abs(start_tt_2(:,q));
start_a = db(start_a/max(start_a));
figure,plot(start_a),ylim([-35,0])% 距离向相位
start_r_p = rad2deg(angle(start_tt_2(p(q),:)));
figure,plot(start_r_p),xlim([0,16*len])% 方位向相位
start_a_p = rad2deg(angle(start_tt_2(:,q)));
figure,plot(start_a_p),xlim([0,16*len])

这篇关于《合成孔径雷达成像算法与实现》Figure6.18的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/714728。

相关文章

C++使用栈实现括号匹配的代码详解

C++使用栈实现括号匹配的代码详解

《C++使用栈实现括号匹配的代码详解》在编程中,括号匹配是一个常见问题,尤其是在处理数学表达式、编译器解析等任务时,栈是一种非常适合处理此类问题的数据结构,能够精确地管理括号的匹配问题,本文将通过C+... 目录引言问题描述代码讲解代码解析栈的状态表示测试总结引言在编程中，括号匹配是一个常见问题，尤其是在
阅读更多...
Java实现检查多个时间段是否有重合

Java实现检查多个时间段是否有重合

《Java实现检查多个时间段是否有重合》这篇文章主要为大家详细介绍了如何使用Java实现检查多个时间段是否有重合,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录流程概述步骤详解China编程步骤1：定义时间段类步骤2：添加时间段步骤3：检查时间段是否有重合步骤4：输出结果示例代码结语作
阅读更多...
使用C++实现链表元素的反转

使用C++实现链表元素的反转

《使用C++实现链表元素的反转》反转链表是链表操作中一个经典的问题,也是面试中常见的考题,本文将从思路到实现一步步地讲解如何实现链表的反转,帮助初学者理解这一操作,我们将使用C++代码演示具体实现,同... 目录问题定义思路分析代码实现带头节点的链表代码讲解其他实现方式时间和空间复杂度分析总结问题定义给定
阅读更多...
Java覆盖第三方jar包中的某一个类的实现方法

Java覆盖第三方jar包中的某一个类的实现方法

《Java覆盖第三方jar包中的某一个类的实现方法》在我们日常的开发中,经常需要使用第三方的jar包,有时候我们会发现第三方的jar包中的某一个类有问题,或者我们需要定制化修改其中的逻辑,那么应该如何... 目录一、需求描述二、示例描述三、操作步骤四、验证结果五、实现原理一、需求描述需求描述如下：需要在
阅读更多...
如何使用Java实现请求deepseek

如何使用Java实现请求deepseek

《如何使用Java实现请求deepseek》这篇文章主要为大家详细介绍了如何使用Java实现请求deepseek功能,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录1.deepseek的api创建2.Java实现请求deepseek2.1 pom文件2.2 json转化文件2.2
阅读更多...
python使用fastapi实现多语言国际化的操作指南

python使用fastapi实现多语言国际化的操作指南

《python使用fastapi实现多语言国际化的操作指南》本文介绍了使用Python和FastAPI实现多语言国际化的操作指南,包括多语言架构技术栈、翻译管理、前端本地化、语言切换机制以及常见陷阱和... 目录多语言国际化实现指南项目多语言架构技术栈目录结构翻译工作流1. 翻译数据存储2. 翻译生成脚本
阅读更多...
如何通过Python实现一个消息队列

如何通过Python实现一个消息队列

《如何通过Python实现一个消息队列》这篇文章主要为大家详细介绍了如何通过Python实现一个简单的消息队列,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录如何通过 python 实现消息队列如何把 http 请求放在队列中执行1. 使用 queue.Queue 和 reque
阅读更多...
Python如何实现PDF隐私信息检测

Python如何实现PDF隐私信息检测

《Python如何实现PDF隐私信息检测》随着越来越多的个人信息以电子形式存储和传输,确保这些信息的安全至关重要,本文将介绍如何使用Python检测PDF文件中的隐私信息,需要的可以参考下... 目录项目背景技术栈代码解析功能说明运行结php果在当今，数据隐私保护变得尤为重要。随着越来越多的个人信息以电子形
阅读更多...
使用 sql-research-assistant进行 SQL 数据库研究的实战指南(代码实现演示)

使用 sql-research-assistant进行 SQL 数据库研究的实战指南(代码实现演示)

《使用sql-research-assistant进行SQL数据库研究的实战指南(代码实现演示)》本文介绍了sql-research-assistant工具,该工具基于LangChain框架,集... 目录技术背景介绍核心原理解析代码实现演示安装和配置项目集成LangSmith 配置（可选）启动服务应用场景
阅读更多...
使用Python快速实现链接转word文档

使用Python快速实现链接转word文档

《使用Python快速实现链接转word文档》这篇文章主要为大家详细介绍了如何使用Python快速实现链接转word文档功能,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 演示代码展示from newspaper import Articlefrom docx import
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2