本文主要是介绍456. 车站分级(拓扑排序,虚拟点建图),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
活动 - AcWing
一条单向的铁路线上,依次有编号为 1, 2, …, n1, 的 n 个火车站。
每个火车站都有一个级别,最低为 1 级。
现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
例如,下表是 5 趟车次的运行情况。
其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。
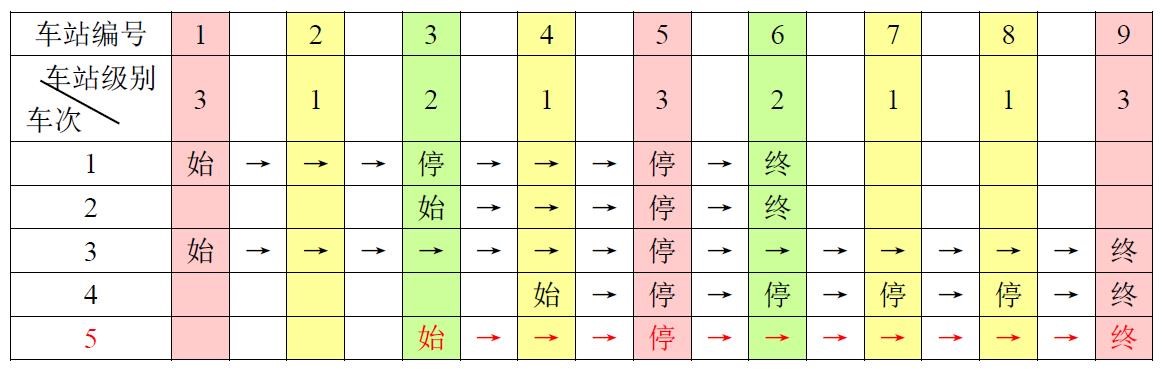
现有 m 趟车次的运行情况(全部满足要求),试推算这 n 个火车站至少分为几个不同的级别。
输入格式
第一行包含 2 个正整数 n,m,用一个空格隔开。
第 i+1 行(1≤i≤m)中,首先是一个正整数 si(2≤si≤n),表示第 i 趟车次有 si 个停靠站;接下来有 si 个正整数,表示所有停靠站的编号,从小到大排列。
每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
输出只有一行,包含一个正整数,即 n 个火车站最少划分的级别数。
数据范围
1≤n,m≤1000
输入样例:
9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
输出样例:
3解析:
依据题目要求,我们可以将每个车次从出发站到终点站内的所有没有停靠的节点向停靠的节点连一条边,权值为1,由于题目一定存在解,所以一定存在拓扑序,只需要依据拓扑序求遍历一遍即可求出答案。
但如果直接按照此思路处理,则所建的边的数量过大,最坏情况下每个车次都要建500*500的边,而有1000 的车次,因此会爆空间。
虚拟点建图:
对于这种将节点分成两个集合,然后其中一个集合中的每一个点都要与另一集合中的每一个点建一条边的图,我们通常会建一个虚拟节点在两个集合中,并且将虚拟节点与其他节点都连上一条边。这种建图方式需要的建的边的数量为 n1+n2(两个集合点的数量),而原来的建图方式需要建 n1*n2。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 2e3 + 5, M = 1e6 + 5, INF = 0x3f3f3f3f;
int n, m;
int h[N], e[M], w[M], ne[M], idx;
int q[N], d[N];
bool st[N];
int dist[N];void add(int a, int b, int c) {e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;d[b]++;
}void topsort() {int hh = 0, tt = 0;for (int i = 1; i <= n+m; i++) {if (!d[i]) {q[tt++] = i;}}while (hh < tt) {int t = q[hh++];for (int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if (--d[j] == 0) {q[tt++] = j;}}}
}int main() {cin >> n >> m;memset(h, -1, sizeof h);for (int i = 1, a; i <= m; i++) {scanf("%d", &a);memset(st, 0, sizeof st);int start = n, end = 1;int u = n + i;for (int j = 1,b; j <= a; j++) {scanf("%d", &b);start = min(start, b);end = max(end, b);st[b] = 1;}for (int j = start; j <= end; j++) {if (st[j])add(u, j, 1);else add(j, u, 0);}}topsort();for (int i = 1; i <= n; i++)dist[i] = 1;for (int i = 0; i < n + m; i++) {int j = q[i];for (int k = h[j]; k != -1; k = ne[k]) {dist[e[k]] = max(dist[e[k]], dist[j] + w[k]);}}int ret = 0;for (int i = 1; i <= n; i++)ret = max(ret, dist[i]);printf("%d\n", ret);return 0;
}
这篇关于456. 车站分级(拓扑排序,虚拟点建图)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






