本文主要是介绍机器学习(二)Apriori算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最近看了《机器学习实战》中的第11章(使用Apriori算法进行关联分析)和第12章(使用FP-growth算法来高效发现频繁项集)。正如章节标题所示,这两章讲了无监督机器学习方法中的关联分析问题。关联分析可以用于回答”哪些商品经常被同时购买?”之类的问题。书中举了一些关联分析的例子:
通过查看哪些商品经常在一起购买,可以帮助商店了解用户的购买行为。这种从数据海洋中抽取的知识可以用于商品定价、市场促销、存活管理等环节。
在美国国会投票记录中发现关联规则。在一个国会投票记录的数据集中发现议案投票的相关性,(原文:这里只是出于娱乐的目的,不过也可以……)使用分析结果来为政治竞选活动服务,或者预测选举官员会如何投票。
发现毒蘑菇的相似特征。这里只对包含某个特定元素(有毒性)的项集感兴趣,从中寻找毒蘑菇中的一些公共特征,利用这些特征来避免吃到那些有毒蘑菇。
在Twitter源中发现一些共现词。对于给定搜索词,发现推文中频繁出现的单词集合。
从新闻网站点击流中挖掘新闻流行趋势,挖掘哪些新闻广泛被用户浏览到。
搜索引擎推荐,在用户输入查询词时推荐同相关的查询词项。
从大规模数据集中寻找物品间的隐含关系被称作关联分析(association analysis)或者关联规则学习(association rule learning)。这里的主要问题在于,寻找物品的不同组合是一项十分耗时的任务,所需的计算代价很高,蛮力搜索方法并不能解决这个问题,所以需要用更智能的方法在合理的时间范围内找到频繁项集。本文分别介绍如何使用Apriori算法来解决上述问题。
1. 关联分析
关联分析是在大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式:
- 频繁项集
- 关联规则
频繁项集(frequent item sets)是经常出现在一块儿的物品的集合,关联规则(association rules)暗示两种物品之间可能存在很强的关系。
下面用一个例子来说明这两种概念:图1给出了某个杂货店的交易清单。
| 交易号码 | 商品 |
|---|---|
| 0 | 豆奶,莴苣 |
| 1 | 莴苣,尿布,葡萄酒,甜菜 |
| 2 | 豆奶,尿布,葡萄酒,橙汁 |
| 3 | 莴苣,豆奶,尿布,葡萄酒 |
| 4 | 莴苣,豆奶,尿布,橙汁 |
图1 某杂货店交易清单
频繁项集是指那些经常出现在一起的商品集合,图中的集合{葡萄酒,尿布,豆奶}就是频繁项集的一个例子。从这个数据集中也可以找到诸如尿布->葡萄酒的关联规则,即如果有人买了尿布,那么他很可能也会买葡萄酒。
我们用支持度和可信度来度量这些有趣的关系。一个项集的支持度(support)被定义数据集中包含该项集的记录所占的比例。如上图中,{豆奶}的支持度为4/5,{豆奶,尿布}的支持度为3/5。支持度是针对项集来说的,因此可以定义一个最小支持度,而只保留满足最小值尺度的项集。
可信度或置信度(confidence)是针对关联规则来定义的。规则{尿布}➞{啤酒}的可信度被定义为”支持度({尿布,啤酒})/支持度({尿布})”,由于{尿布,啤酒}的支持度为3/5,尿布的支持度为4/5,所以”尿布➞啤酒”的可信度为3/4。这意味着对于包含”尿布”的所有记录,我们的规则对其中75%的记录都适用。
2. Apriori原理
假设我们有一家经营着4种商品(商品0,商品1,商品2和商品3)的杂货店,2图显示了所有商品之间所有的可能组合:
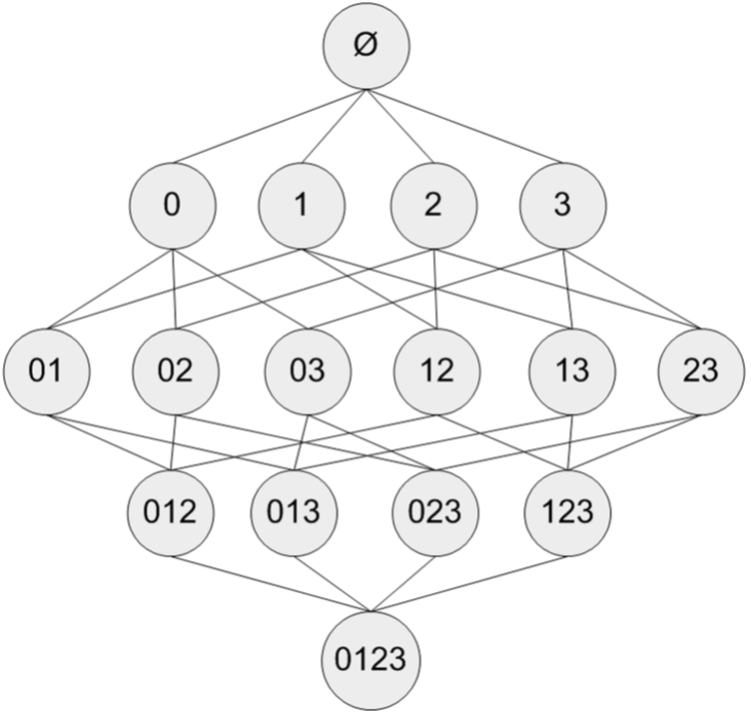
图2 集合{0,1,2,3,4}中所有可能的项集组合
对于单个项集的支持度,我们可以通过遍历每条记录并检查该记录是否包含该项集来计算。对于包含N中物品的数据集共有2N−12N−1种项集组合,重复上述计算过程是不现实的。
研究人员发现一种所谓的Apriori原理,可以帮助我们减少计算量。Apriori原理是说如果某个项集是频繁的,那么它的所有子集也是频繁的。更常用的是它的逆否命题,即如果一个项集是非频繁的,那么它的所有超集也是非频繁的。
在图3中,已知阴影项集{2,3}是非频繁的。利用这个知识,我们就知道项集{0,2,3},{1,2,3}以及{0,1,2,3}也是非频繁的。也就是说,一旦计算出了{2,3}的支持度,知道它是非频繁的后,就可以紧接着排除{0,2,3}、{1,2,3}和{0,1,2,3}。
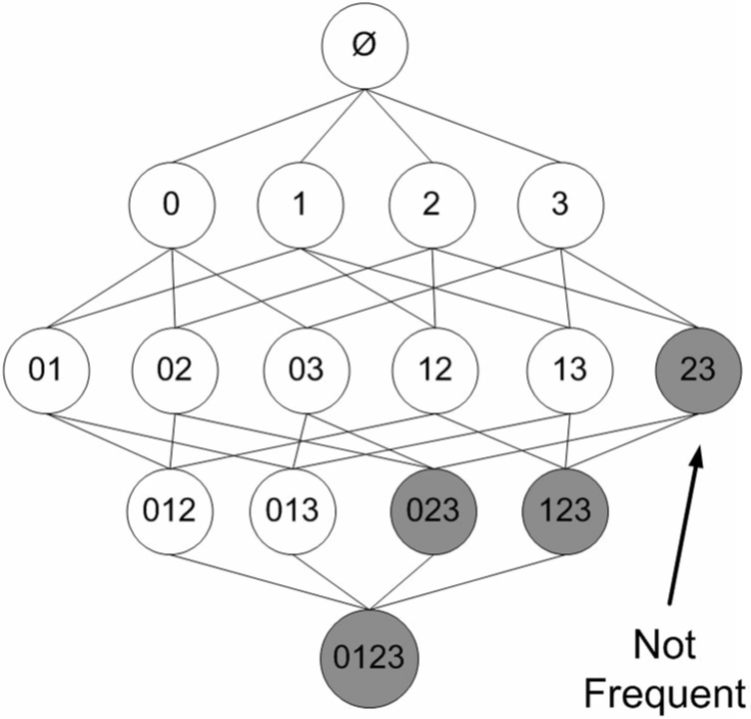
图3 图中给出了所有可能的项集,其中非频繁项集用灰色表示。
3. 使用Apriori算法来发现频繁集
前面提到,关联分析的目标包括两项:发现频繁项集和发现关联规则。首先需要找到频繁项集,然后才能获得关联规则(正如前文所讲,计算关联规则的可信度需要用到频繁项集的支持度)。
Apriori算法是发现频繁项集的一种方法。Apriori算法的两个输入参数分别是最小支持度和数据集。该算法首先会生成所有单个元素的项集列表。接着扫描数据集来查看哪些项集满足最小支持度要求,那些不满足最小支持度的集合会被去掉。然后,对剩下来的集合进行组合以生成包含两个元素的项集。接下来,再重新扫描交易记录,去掉不满足最小支持度的项集。该过程重复进行直到所有项集都被去掉。
3.1 生成候选项集
数据集扫描的伪代码大致如下:
对数据集中的每条交易记录tran:
对每个候选项集can:检查can是否是tran的子集如果是,则增加can的计数
对每个候选项集:
如果其支持度不低于最小值,则保留该项集
返回所有频繁项集列表
下面看一下实际代码,建立一个apriori.py文件并加入一下代码:
# coding=utf-8
from numpy import *def loadDataSet():return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]其中numpy为程序中需要用到的Python库:
def createC1(dataSet):C1 = []for transaction in dataSet:for item in transaction:if not [item] in C1:C1.append([item])C1.sort()return map(frozenset, C1)其中C1即为元素个数为1的项集(非频繁项集,因为还没有同最小支持度比较)。map(frozenset, C1)的语义是将C1由Python列表转换为不变集合(frozenset,Python中的数据结构)。
def scanD(D, Ck, minSupport):ssCnt = {}for tid in D:for can in Ck:if can.issubset(tid):ssCnt[can] = ssCnt.get(can, 0) + 1numItems = float(len(D))retList = []supportData = {}for key in ssCnt:support = ssCnt[key] / numItemsif support >= minSupport:retList.insert(0, key)supportData[key] = supportreturn retList, supportData其中D为全部数据集,Ck为大小为k(包含k个元素)的候选项集,minSupport为设定的最小支持度。返回值中retList为在Ck中找出的频繁项集(支持度大于minSupport的),supportData记录各频繁项集的支持度。
retList.insert(0, key)一行将频繁项集插入返回列表的首部。
3.2 完整的Apriori算法
当集合中项的个数大于0时:构建一个由k个项组成的候选项集的列表(k从1开始)计算候选项集的支持度,删除非频繁项集构建由k+1项组成的候选项集的列表
程序代码如下:
def aprioriGen(Lk, k):retList = []lenLk = len(Lk)for i in range(lenLk):for j in range(i + 1, lenLk):# 前k-2项相同时,将两个集合合并L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]L1.sort(); L2.sort()if L1 == L2:retList.append(Lk[i] | Lk[j])return retList该函数通过频繁项集列表 Lk 和项集个数k生成候选项集 Ck+1 。
注意其生成的过程中,首选对每个项集按元素排序,然后每次比较两个项集,只有在前k-1项相同时才将这两项合并。这样做是因为函数并非要两两合并各个集合,那样生成的集合并非都是k+1项的。在限制项数为k+1的前提下,只有在前k-1项相同、最后一项不相同的情况下合并才为所需要的新候选项集。
由于Python中使用下标0表示第一个元素,因此代码中的[:k-2]的实际作用为取列表的前k-1个元素。
def apriori(dataSet, minSupport=0.5):C1 = createC1(dataSet)D = map(set, dataSet)L1, supportData = scanD(D, C1, minSupport)L = [L1]k = 2while (len(L[k-2]) > 0):Ck = aprioriGen(L[k-2], k)Lk, supK = scanD(D, Ck, minSupport)supportData.update(supK)L.append(Lk)k += 1return L, supportData该函数为Apriori算法的主函数,按照前述伪代码的逻辑执行。Ck表示项数为k的候选项集,最初的C1通过createC1()函数生成。Lk表示项数为k的频繁项集,supK为其支持度,Lk和supK由scanD()函数通过Ck计算而来。
函数返回的L和supportData为所有的频繁项集及其支持度,因此在每次迭代中都要将所求得的Lk和supK添加到L和supportData中。
代码测试(在Python提示符下输入):
>>> import apriori
>>> dataSet = apriori.loadDataSet()
>>> dataSet
>>> C1 = apriori.createC1(dataSet)
>>> D = map(set, dataSet)
>>> D
>>> L1, suppDat = apriori.scanD(D, C1, 0.5)
>>> L1
>>> L, suppData = apriori.apriori(dataSet)
>>> L
>>> L, suppData = apriori.apriori(dataSet, minSupport=0.7)
>>> LL返回的值为frozenset列表的形式:
[[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])],
[frozenset([1, 3]), frozenset([2, 5]), frozenset([2, 3]), frozenset([3, 5])],
[frozenset([2, 3, 5])], []]
即L[0]为项数为1的频繁项集:
[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]
L[1]为项数为2的频繁项集:
[frozenset([1, 3]), frozenset([2, 5]), frozenset([2, 3]), frozenset([3, 5])]
依此类推。
suppData为一个字典,它包含项集的支持度。
3.3 从频繁集中挖掘相关规则
解决了频繁项集问题,下一步就可以解决相关规则问题。
要找到关联规则,我们首先从一个频繁项集开始。从杂货店的例子可以得到,如果有一个频繁项集{豆奶, 莴苣},那么就可能有一条关联规则“豆奶➞莴苣”。这意味着如果有人购买了豆奶,那么在统计上他会购买莴苣的概率较大。注意这一条反过来并不总是成立,也就是说,可信度(“豆奶➞莴苣”)并不等于可信度(“莴苣➞豆奶”)。
前文也提到过,一条规则P➞H的可信度定义为support(P | H)/support(P),其中“|”表示P和H的并集。可见可信度的计算是基于项集的支持度的。
图4给出了从项集{0,1,2,3}产生的所有关联规则,其中阴影区域给出的是低可信度的规则。可以发现如果{0,1,2}➞{3}是一条低可信度规则,那么所有其他以3作为后件(箭头右部包含3)的规则均为低可信度的。
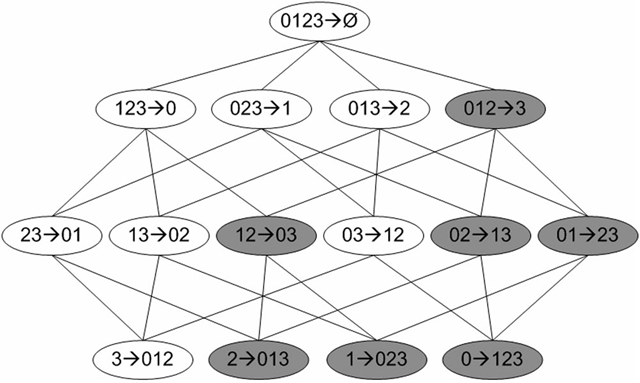
图4 频繁项集{0,1,2,3}的关联规则网格示意图
可以观察到,如果某条规则并不满足最小可信度要求,那么该规则的所有子集也不会满足最小可信度要求。以图4为例,假设规则{0,1,2} ➞ {3}并不满足最小可信度要求,那么就知道任何左部为{0,1,2}子集的规则也不会满足最小可信度要求。可以利用关联规则的上述性质属性来减少需要测试的规则数目,类似于Apriori算法求解频繁项集。
4. 小结
关联分析是用于发现大数据集中元素间有趣关系的一个工具集,可以采用两种方式来量化这些有趣的关系。第一种方式是使用频繁项集,它会给出经常在一起出现的元素项。第二种方式是关联规则,每条关联规则意味着元素项之间的“如果……那么”关系。
发现元素项间不同的组合是个十分耗时的任务,不可避免需要大量昂贵的计算资源,这就需要一些更智能的方法在合理的时间范围内找到频繁项集。能够实现这一目标的一个方法是Apriori算法,它使用Apriori原理来减少在数据库上进行检查的集合的数目。Apriori原理是说如果一个元素项是不频繁的,那么那些包含该元素的超集也是不频繁的。Apriori算法从单元素项集开始,通过组合满足最小支持度要求的项集来形成更大的集合。支持度用来度量一个集合在原始数据中出现的频率。
关联分析可以用在许多不同物品上。商店中的商品以及网站的访问页面是其中比较常见的例子。
每次增加频繁项集的大小,Apriori算法都会重新扫描整个数据集。当数据集很大时,这会显著降低频繁项集发现的速度。下面会介绍FP-growth算法,和Apriori算法相比,该算法只需要对数据库进行两次遍历,能够显著加快发现频繁项集的速度。
这篇关于机器学习(二)Apriori算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








