本文主要是介绍python实现自顶向下的句法分析和基于CYK算法的句法分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题描述
- 构建基于自顶向下的句法分析器,对输入串“孩子/n 喜欢/v 狗/n”,采用以下文法进行句法分析,得到输入串的句法分析过程。
(1.1) S→NP VP
(1.2) S→VP
(2.1) NP→n
(2.2) NP→a n
(3.1) VP→v NP - 构建基于CYK算法的句法分析器,对输入串“张三/n 是/v 县长/n 派/v 来/v 的/de”,采用以下文法进行句法分析,得到输入串对应的句法分析结果。
① S→NP VP
② NP→n
③ NP→CS de
④ CS→NP V’
⑤ VP→v NP
⑥ V’→v v
文章目录
- 问题描述
- 自顶向下句法分析
- 简介
- 实验结果
- CYK算法
- 处理过程
- 实验结果
自顶向下句法分析
简介
一种语言的文法可以表示为一个四元组:G=<T,N,P,S>,其中T为终结符集合(用来表示词类),N为非终结符集合(用来表示语法成分),P为产生式(用来表示句法规则),S为起始符,它是N的一个元素。
自顶向下的分析是从树根开始推导的,它作用于如下形式的推导:S–>z1–>z2–>…–>zn,开始的时候,这个推导只包含起始符S,并且n=0。所用到的规则放在一个先进先出的堆栈里,开始时堆栈为空,这个堆栈的作用是记录最近所用到的规则的作用。
因为给出的字符串是汉字加词性的组合,所以要对这个字符串进行处理,分别获得汉字和词性,最主要的是要获得到词性,因为这些句法分析是建立在这些字符上的操作,分为终结符和非终结符,对这些词性进行处理。
示例如下:
rules = [ # 规则('S', 'NP VP'),('S', 'VP'),('NP', 'n'),('NP', 'an'),('VP', 'v NP')
]
s = '孩子/an 喜欢/v 狗/n' # 输入词串
t1 = s.split() # 词串列表
t = []
word = []
for it in t1:word.extend(it.split('/'))t.append(word.pop())
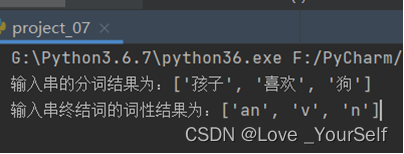
然后对这获得到的词性列表之后进行处理,一条“产生式”就是一条句法规则。不同类型的文法对规则的形式有不同的限制。句法分析前首先要确定使用什么类型的文法。S作为最开始的符号,通过产生式不断的替换非终结符,得到最后的处理结果。
实验结果
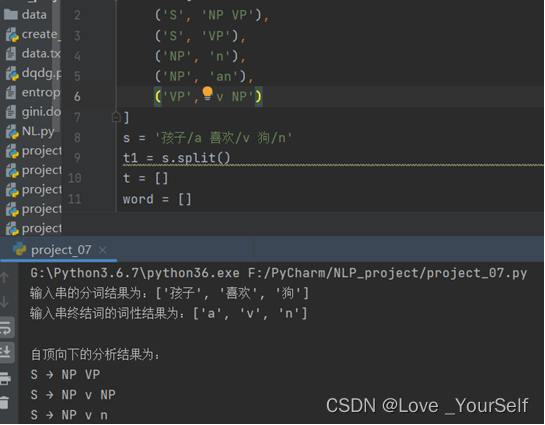
然后修改n设置为an之后再次测试得到的结果如下,证实了算法的可用性
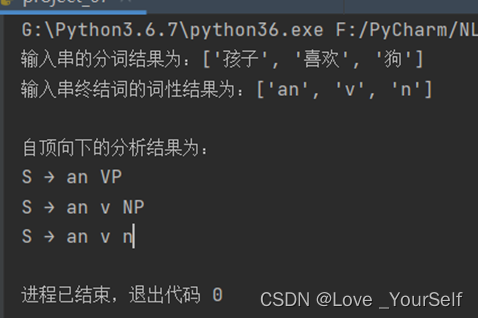
然后再修改字符串,使用到第二条S的产生式,得到的结果如下
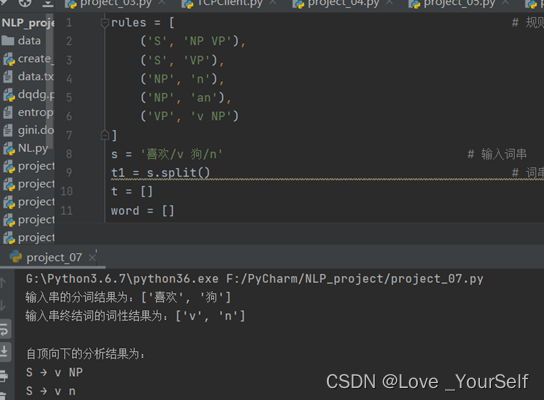
CYK算法
处理过程
初始化:对i=0, j=0,…,n-1, 将输入串中的符号tj填入P(i,j)
- 构造规则列表,以元组形式存放文法
- 将输入串切分为单词列表
- 记录单词列表和文法列表的长度
- 构造分析表矩阵
rules = [ # 规则('S', 'NP VP'),('NP', 'n'),('NP', 'CS de'),('CS', 'NP V1'),('VP', 'v NP'),('V1', 'v v')
]
s = '张三/n 是/v 县长/n 派/v 来/v 的/de' # 输入词串
t1 = s.split() # 词串列表
t = []
word = []
for it in t1:word.extend(it.split('/'))t.append(word.pop())
print('输入串的分词结果为:' + str(word))
print('输入串终结词的词性结果为:' + str(t))n = len(t) # 词串个数
nRules = len(rules)
P = [[set() for j in range(n-i)] for i in range(n)] # 矩阵# 初始化:对i=0, j=0,···,n-1, 将输入串中的符号tj填入P(i,j)
for j in range(n):P[0][j].add(t[j])初始化后的“三角矩阵”:
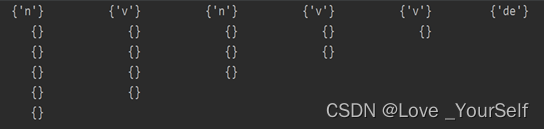
第1步:对i=0, j=0,…,n-1,若有规则A->tj, 则将非终结符A加入P(i,j);
即遍历分析表矩阵的第0行,同时判断文法中产生式的右边元素是否在其中,若在其中,则将对应产生式的非终结符加入P(0,j)
for j in range(n):for r in range(nRules):if rules[r][1] in P[0][j]:P[0][j].add(rules[r][0])第一步之后,第一行添加完毕:
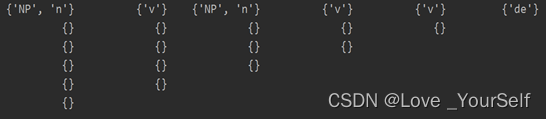
第2步:对i=1,…,n-1, j=0,1,…,n-i-1, k=0,…,i-1, 对每一条规则A->BC,若B∈P(k,j) 且 C∈P(i-k-1,j+k+1),则将非终结符A加入P(i,j);
首先需要将产生式规则的右部进行处理,因为rules以元组形式存放,故将rules[r][1]取出并进行分词,构成一个元素放入列表。
再构造多重循环判断条件是否成立
ruleList = []
for r in range(nRules):result = rules[r][1].split()if len(result) == 1:result.append('null')ruleList.append(result)
# print(ruleList)
for i in range(1, n):for j in range(0, n-i):for k in range(0, i):for r in range(nRules):if (ruleList[r][0] in P[k][j]) and (ruleList[r][1] in P[i-k-1][j+k+1]):P[i][j].add(rules[r][0])将产生式的右边取出并转换为列表:

将每一次循环得到的结果输出:

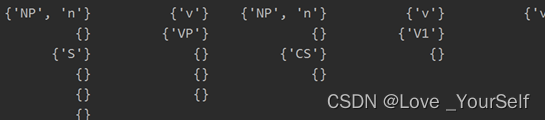



第3步:若S∈P(n-1,0), 则分析成功,否则分析失败。
if 'S' in P[n-1][0]:print('分析成功')
else:print('分析失败')实验结果
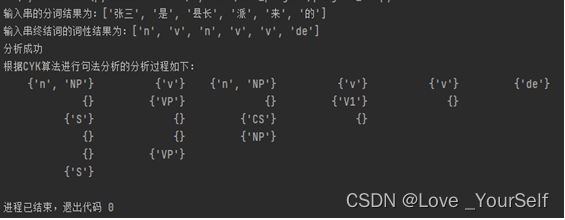
这篇关于python实现自顶向下的句法分析和基于CYK算法的句法分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





