本文主要是介绍FDD-MU-mMIMO下针对快速波束训练的用户协同,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 背景
- 系统模型
- 基于GoB的信道估计
- 数据信号模型
- 最优预编码器与合并器设计问题
- 数据波束成形设计
- GoD波束成形设计
- 最大化有效信道增益
- 最小化用户间干扰
- 最小化训练开销
- 去中心化的协同波束选择算法
- 仿真结果分析
- 仿真场景参数:
- 仿真结果
- 吞吐量 v.s. SNR
- 相对增益 v.s.信道相关时间
- 吞吐量 v.s. 反馈量化比特
本文是对 User Coordination for Fast Beam Training in FDD Multi-User Massive MIMO的摘记。
背景
Massive multiple-input multiple-output (mMIMO) 是5G/B5G通信中重要的一个技术。在许多TDD制式下的mMIMO技术已经显著地提升了系统容量。在FDD中考虑mMIMO的两个主要困难是下行参考信号的可扩展性,以及与信道状态信息(CSI)获取所需的上行反馈相关的开销。
在TDD网络中,通过低开销的上行探测(Sounding )信号利用信道互易性(channel reciprocity)可以实现一个接近最优的线性与编码器。
而在FDD网络中,其不存在信道互易性,需要参考信号(Reference Signals, RSs)和随后的上行反馈来估计下行信道,这使得其具有相当大的挑战性。一般来说,RSs和天线单元之间存在一一对应关系。因此,在FDD mMIMO体制下训练和反馈开销通常觉得是不可行的,因为这样只有少量的资源留给数据传输。
考虑FDD仍然是有意义的,几个原因如下:
- Sub-6GHz的无线电频段都是对称FDD频段。
- 由于FDD网络中需要的基站较少,从而降低了总体部署、维护和运营成本。
解决FDD mMIMO中的开销问题的方法总体可以分为三种:
- 基于二阶统计的方法
- 基于压缩感知的方法
- 基于信道外推(channel extrapolation)的方法
- 基于波束网格的(grid-of-beams, GoB)方法
由于GoB实际的可实施性,其3GPP论坛中引起了广泛地关注,该想法再次将高维的信道转化为了低维信道,通过基于固定发射接收波束的空间变换,可以得到简化的信道表示。因此,UE看到的低维等效信道包含了与波束相关的波束成形向量。
- 注意:估计这种等效信道可以减少训练开销,因为它与码本大小成正比,而与天线单元的数量无关。即使下行信道不存在稀疏表示,GoB方法也允许低维表示。
- 由于GoB的训练(和反馈)开销的减少将导致可能严重的性能下降,因为mMIMO数据预编码器优化了减少的信道表示,这可能无法捕捉到实际无线信道的显著特征。
为了减少基于GoB方法的性能损失,另一个可行的办法是用大量的波束设计GoB,然后训练其中的一小部分(包含最相关的信道成分,但通常是超出了设计者的控制范围)。在UE侧是多天线时,UE侧的统计波束形成(协方差整形)可以用来激励理想的信道子空间,使得能量进入合适的空间区域以获得额外的自由度。 一般来说,在BS和UE两侧激活哪些波束的决定不是一个简单的问题,因为有几个因素参与了求和速率优化问题,包括i)波束形成增益,ii)多用户干扰,iii)训练开销。此外,波束选择是一个在UEs和BS之间的理想联合决策问题,协调问题随之而来。
本文主要讨论基于GoB的方法,而i,i,iii也是本文设计的核心思想。
系统模型
考虑单小区多用户场景,mMIMO基站配备 N B s ≫ 1 N_{Bs}\gg1 NBs≫1根天线服务(下行传输) K ≪ N B S K \ll N_{\mathrm{BS}} K≪NBS个用户,且每个用户配备有 N U E N_{UE} NUE根天线。假设信号在传输到所有终端之前使用线性预编码技术对其进行处理,且考虑FDD制式(上下行信道不在具有互易性)。
关注一个有趣的例子:
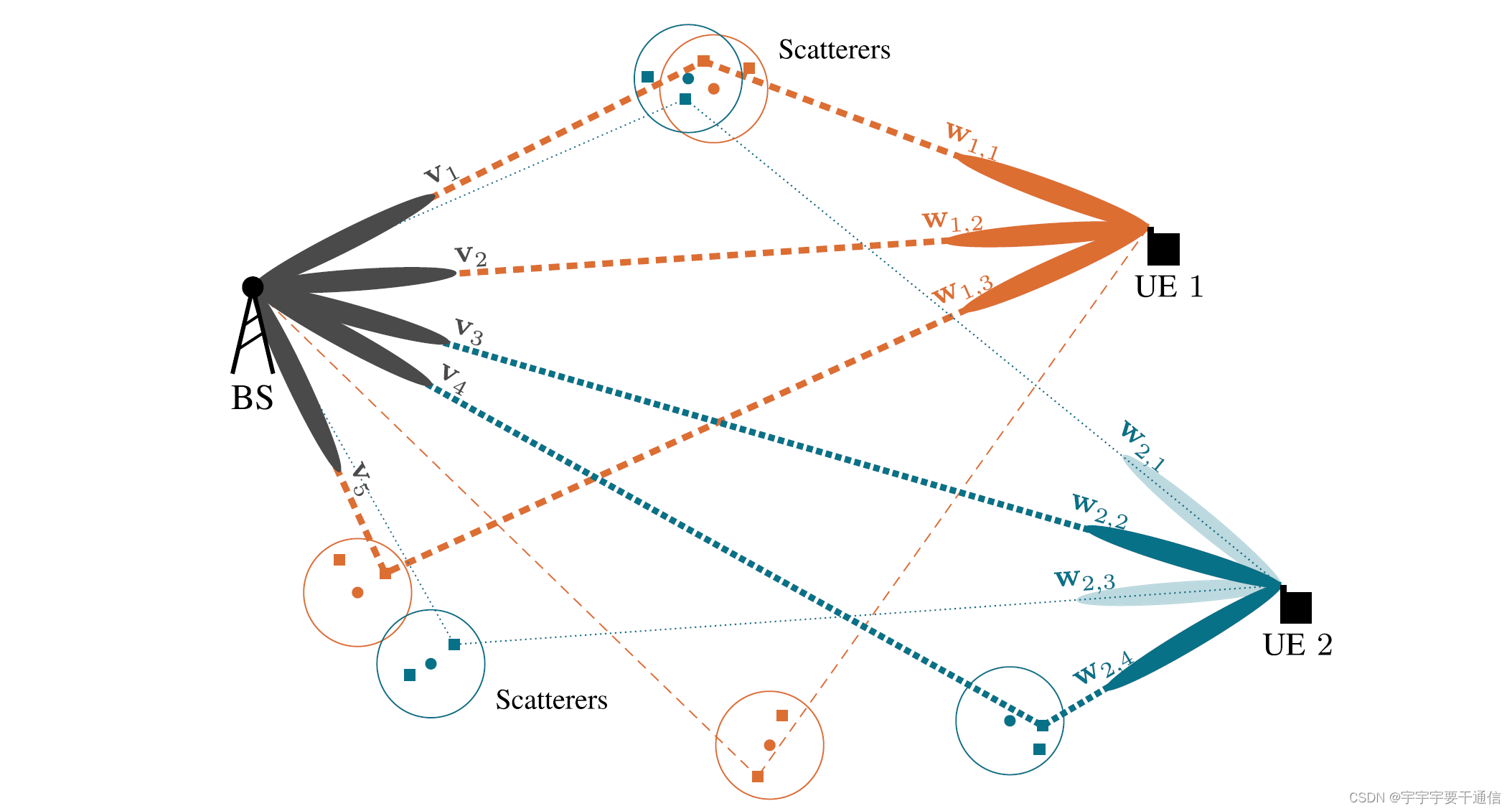
图中BS服务两个UE,蓝色和橙色的圆圈表示多路径簇(或散射体),它们可能被某些UE共享。更强的路径用粗体标出。
传统的基于max-SNR波束选择策略会收集最多的能量但其将导致在BS侧有 M B S = 5 M_{BS}=5 MBS=5个波束要训练。考虑另一种方式:UE2优化较弱的 w 2 , 1 \mathbf{w}_{2,1} w2,1和 w 2 , 3 \mathbf{w}_{2,3} w2,3,而U1继续激活它的三个强波束。这种策略收集了较少的能量,但于在BS端需要激活的波束下降为了 M B S = 3 M_{BS}=3 MBS=3导致减少了40%的训练开销。,这样实现的机理是:在BS侧的 v 1 \mathbf{v}_1 v1、 v 2 \mathbf{v}_2 v2和 v 5 \mathbf{v}_5 v5波束同时服务于UE1和UE2,并保持它们之间的可分离性。
基于GoB的信道估计
定义BS和UE的波束码本为:
B B S ≜ { v 1 , … , v B B S } , B U E ≜ { w 1 , … , w B U E } \mathcal{B}_{\mathrm{BS}} \triangleq\left\{\mathbf{v}_{1}, \ldots, \mathbf{v}_{B_{\mathrm{BS}}}\right\}, \quad \mathcal{B}_{\mathrm{UE}} \triangleq\left\{\mathbf{w}_{1}, \ldots, \mathbf{w}_{B_{\mathrm{UE}}}\right\} BBS≜{v1,…,vBBS},BUE≜{w1,…,wBUE}
其中: card ( B B S ) = B B S \operatorname{card}\left(\mathcal{B}_{\mathrm{BS}}\right)=B_{\mathrm{BS}} card(BBS)=BBS和 card ( B U E ) = B U E \operatorname{card}\left(\mathcal{B}_{\mathrm{UE}}\right)=B_{\mathrm{UE}} card(BUE)=BUE,且 v v ∈ C N B S × 1 , v ∈ { 1 , … , B B S } \mathbf{v}_{v} \in \mathbb{C}^{N_{\mathrm{BS}} \times 1}, \quad v \in\left\{1, \ldots, B_{\mathrm{BS}}\right\} vv∈CNBS×1,v∈{1,…,BBS}表示 B B S \mathcal{B}_{\mathrm{BS}} BBS中的波束成形向量, w w ∈ C N U E × 1 , w ∈ { 1 , … , B U E } \mathbf{w}_{w} \in \mathbb{C}^{N_{\mathrm{UE}} \times 1}, \quad w \in\left\{1, \ldots, B_{\mathrm{UE}}\right\} ww∈CNUE×1,w∈{1,…,BUE}。(为了符号的简洁,假设所有用户的码本是一样的,很容易推广到用户不一样码本的情况)。
考虑NR基于OFDM的调制方案。考虑一个包含了 T T T个资源单元的资源网格,其中 τ M B S \tau M_{\mathrm{BS}} τMBS被分配给RSs, T − τ M B S T-\tau M_{\mathrm{BS}} T−τMBS分配给数据传输( M B S M_\mathrm{BS} MBS表示在 B B S \mathcal{B}_{\mathrm{BS}} BBS中被训练的波束数量, τ \tau τ用相关RSs的OFDM符号的数量来测量的持续时间 ,即:一个RS对应一个波束。具体参考下图)

第 k k k个UE的接收训练信号 Y k ∈ C M U E × τ \mathbf{Y}_{k} \in \mathbb{C}^{M_{\mathrm{UE}} \times \tau} Yk∈CMUE×τ表示为( M U E M_{\mathrm{UE}} MUE为UE侧的活跃波束):
Y k = ρ W k H H k V S + W k H N k , ∀ k ∈ { 1 , … , K } \mathbf{Y}_{k}=\rho \mathbf{W}_{k}^{\mathrm{H}} \mathbf{H}_{k} \mathbf{V S}+\mathbf{W}_{k}^{\mathrm{H}} \mathbf{N}_{k}, \quad \forall k \in\{1, \ldots, K\} Yk=ρWkHHkVS+WkHNk,∀k∈{1,…,K}
其中, S ∈ C M B S × τ \mathbf{S} \in \mathbb{C}^{M_{\mathrm{BS}} \times \tau} S∈CMBS×τ包含了正交的RSs(已知)且 S S H = I M B S \mathbf{S S}^{\mathrm{H}}=\mathbf{I}_{M_{\mathrm{BS}}} SSH=IMBS, V ≜ [ v 1 … v M B S ] ∈ C N B S × M B S \mathbf{V} \triangleq\left[\mathbf{v}_{1} \ldots \mathbf{v}_{M_{\mathrm{BS}}}\right] \in \mathbb{C}^{N_{\mathrm{BS}} \times M_{\mathrm{BS}}} V≜[v1…vMBS]∈CNBS×MBS是对于所有UE共有的归一化训练(GoB)预编码器。 H k ∈ C N U E × N B S \mathbf{H}_{k} \in \mathbb{C}^{N_{\mathrm{UE}} \times N_{\mathrm{BS}}} Hk∈CNUE×NBS是第 k k k个UE和BS之间的信道矩阵,且 vec ( H k ) ∼ C N ( 0 , Σ k ) \operatorname{vec}\left(\mathbf{H}_{k}\right) \sim \mathcal{C N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{k}\right) vec(Hk)∼CN(0,Σk)和 Σ k ∈ C N B S N U E × N B S N U E \mathbf{\Sigma}_{k} \in \mathbb{C}^{N_{\mathrm{BS}} N_{\mathrm{UE}} \times N_{\mathrm{BS}} N_{\mathrm{UE}}} Σk∈CNBSNUE×NBSNUE是相关的信道协方差矩阵(假设已知)。 W k ≜ [ w k , 1 … w k , M U E ] ∈ C N U E × M U E \mathbf{W}_{k} \triangleq\left[\mathbf{w}_{k, 1} \ldots \mathbf{w}_{k, M_{\mathrm{UE}}}\right] \in \mathbb{C}^{N_{\mathrm{UE}} \times M_{\mathrm{UE}}} Wk≜[wk,1…wk,MUE]∈CNUE×MUE是第 k k k个用户的训练合并器。(注意: V \mathbf{V} V和 W k ∀ k \mathbf{W}_{k} \forall k Wk∀k都包含在预先定义的GoB B B S \mathcal{B}_{\mathrm{BS}} BBS和 B U E \mathcal{B}_{\mathrm{UE}} BUE码本中。)。 N k ∈ C N U E × τ \mathbf{N}_{k} \in \mathbb{C}^{N_{\mathrm{UE}} \times \tau} Nk∈CNUE×τ是第 k k k个用户的接收噪声,每个元素满足独立同分布 C N ( 0 , σ n 2 ) \mathcal{C N}\left(0, \sigma_{n}^{2}\right) CN(0,σn2)。 ρ ≜ P / T \rho \triangleq \sqrt{P / T} ρ≜P/T。P是在考虑的相干(在时间和子载波上)帧中,在BS处可用的总发射功率。
训练阶段结束后,UE可以估计他们的瞬时GoB等效信道为:
H ‾ k ≜ W k H H k V ∈ C M U E × M B S , ∀ k ∈ { 1 , … , K } \overline{\mathbf{H}}_{k} \triangleq \mathbf{W}_{k}^{\mathrm{H}} \mathbf{H}_{k} \mathbf{V} \in \mathbb{C}^{M_{\mathrm{UE}} \times M_{\mathrm{BS}}}, \quad \forall k \in\{1, \ldots, K\} Hk≜WkHHkV∈CMUE×MBS,∀k∈{1,…,K}
并定义其协方差矩阵为 Σ ˉ k ∈ C M B S M U E × M B S M U E , ∀ k ∈ { 1 , … , K } \mathrm{\bar{\Sigma}}_{k} \in\mathbb{C}^{M_{\mathrm{BS}} M_{\mathrm{UE}} \times M_{\mathrm{BS}} M_{\mathrm{UE}}}, \quad \forall k \in\{1, \ldots, K\} Σˉk∈CMBSMUE×MBSMUE,∀k∈{1,…,K}
注:对于信道估计,假设每个UE至少有 M U E M_{\mathrm{UE}} MUE个独立的RF通道能够并行处理接收波束 [ w k , 1 … w k , M U E ] \left[\mathbf{w}_{k, 1} \ldots \mathbf{w}_{k, M_{\mathrm{UE}}}\right] [wk,1…wk,MUE]。
引入一个块对角矩阵 W ∈ C K N U E × K M U E \mathbf{W} \in \mathbb{C}^{KN_{\mathrm{UE}} \times K M_{\mathrm{UE}}} W∈CKNUE×KMUE包含 K K K个用户的GoB合并器:
W ≜ [ W 1 0 ⋱ 0 W K ] \mathbf{W} \triangleq\left[\begin{array}{ccc} \mathbf{W}_{1} & & \mathbf{0} \\ & \ddots & \\ \mathbf{0} & & \mathbf{W}_{K} \end{array}\right] W≜⎣⎡W10⋱0WK⎦⎤
整个多用户的等效信道 H ‾ ∈ C K M U E × M B S \overline{{\mathbf{H}}}\in \mathbb{C}^{KM_{\mathrm{UE}} \times M_{\mathrm{BS}}} H∈CKMUE×MBS可以表示为:
H ‾ ≜ W H H V \overline{\mathbf{H}} \triangleq \mathbf{W}^{\mathrm{H}} \mathbf{H V} H≜WHHV
其中 H ≜ [ H 1 T … H K T ] T ∈ C K N U E × N B S \mathbf{H} \triangleq\left[\mathbf{H}_{1}^{\mathrm{T}} \ldots \mathbf{H}_{K}^{\mathrm{T}}\right]^{\mathrm{T}} \in \mathbb{C}^{K N_{\mathrm{UE}} \times N_{\mathrm{BS}}} H≜[H1T…HKT]T∈CKNUE×NBS表示整个多用户信道。
为了关闭CSI采集回路,每个UE将其估计的有效信道反馈给BS。 随后,基站会获得等效信道 H ‾ \overline{{\mathbf{H}}} H的一个估计值 H ‾ ^ ∈ C K M U E × M B S \hat{\overline{\mathbf{H}}} \in \mathbb{C}^{KM_{\mathrm{UE}} \times M_{\mathrm{BS}}} H^∈CKMUE×MBS来设计数据预编码。假设UEs采用流形的LMMSE估计器,第 k k k个用户的等效信道估计值 H ‾ ^ k \hat{\overline{\mathbf{H}}}_{k} H^k可以表示为:
vec ( H ^ k ) = ρ Σ ‾ k A H ( ρ 2 A Σ ‾ k A H + σ n 2 Γ Γ H ) − 1 vec ( Y k ) \operatorname{vec}\left(\hat{\mathbf{H}}_{k}\right)=\rho \overline{\boldsymbol{\Sigma}}_{k} \mathbf{A}^{\mathrm{H}}\left(\rho^{2} \mathbf{A} \overline{\boldsymbol{\Sigma}}_{k} \mathbf{A}^{\mathrm{H}}+\sigma_{n}^{2} \boldsymbol{\Gamma} \boldsymbol{\Gamma}^{\mathrm{H}}\right)^{-1} \operatorname{vec}\left(\mathbf{Y}_{k}\right) vec(H^k)=ρΣkAH(ρ2AΣkAH+σn2ΓΓH)−1vec(Yk)
其中:
- A ≜ ( S T ⊗ I M U E ) ∈ C τ M U E × M B S M U E \mathbf{A} \triangleq\left(\mathbf{S}^{\mathrm{T}} \otimes \mathbf{I}_{M_{\mathrm{UE}}}\right) \in \mathbb{C}^{\tau M_{\mathrm{UE}} \times M_{\mathrm{BS}} M_{\mathrm{UE}}} A≜(ST⊗IMUE)∈CτMUE×MBSMUE
- Γ ≜ ( I τ ⊗ W k H ) ∈ C τ M U E × τ N U E \boldsymbol{\Gamma} \triangleq\left(\mathbf{I}_{\tau} \otimes \mathbf{W}_{k}^{\mathrm{H}}\right) \in \mathbb{C}^{\tau M_{\mathrm{UE}} \times \tau N_{\mathrm{UE}}} Γ≜(Iτ⊗WkH)∈CτMUE×τNUE
假设第 k k k个用户的信道估计误差表示为: e k = ( vec ( H ‾ k ) − vec ( H ‾ k ) ) \mathbf{e}_{k}=\left(\operatorname{vec}\left(\overline{\mathbf{H}}_{k}\right)-\operatorname{vec}\left(\overline{\mathbf{H}}_{k}\right)\right) ek=(vec(Hk)−vec(Hk)),则估计误差的协方差具体可以表示为:
Σ e k = ( Σ ‾ k − 1 + κ A H ( Γ Γ H ) − 1 A ) − 1 \boldsymbol{\Sigma}_{\mathbf{e}_{k}}=\left(\overline{\boldsymbol{\Sigma}}_{k}^{-1}+\kappa \mathbf{A}^{\mathrm{H}}\left(\boldsymbol{\Gamma} \boldsymbol{\Gamma}^{\mathrm{H}}\right)^{-1} \mathbf{A}\right)^{-1} Σek=(Σk−1+κAH(ΓΓH)−1A)−1
其中,定义 κ ≜ ρ 2 / σ n 2 \kappa \triangleq \rho^{2} / \sigma_{n}^{2} κ≜ρ2/σn2。具体推导可以参考原文。
数据信号模型
数据传输阶段(通过等效信道)将紧随训练和UE反馈阶段。考虑单个资源单元的情况, x k ≜ [ x 1 , 1 … x 1 , L k ] T ∈ C L k × 1 \mathbf{x}_{k} \triangleq \left[x_{1,1} \ldots x_{1, L_{k}}\right]^T \in \mathbb{C}^{L_{k} \times 1} xk≜[x1,1…x1,Lk]T∈CLk×1表示发给第 k k k个用户的数据向量。因此,整个数据向量可以表示为 x ≜ [ x 1 … x K ] T ∈ C L × 1 \mathbf{x} \triangleq\left[\mathbf{x}_{1} \ldots \mathbf{x}_{K}\right]^T \in \mathbb{C}^{L \times 1} x≜[x1…xK]T∈CL×1且 L ≜ ∑ k L k L \triangleq \sum_{k} L_{k} L≜∑kLk是传输数据符号的总数目并满足 E [ x x H ] = I L \mathbb{E}\left[\mathbf{x} \mathbf{x}^{\mathrm{H}}\right]=\mathbf{I}_{L} E[xxH]=IL,则第 k k k个用户的接收数据信号可以表示为:
x ^ k = ρ W ‾ k H H ‾ k V ‾ x + W ‾ k H n ‾ k , ∀ k ∈ { 1 , … , K } = ρ W ‾ k H H ‾ k V ‾ k x k + ∑ j ≠ k ρ W ‾ k H H ‾ k V ‾ j x j + W ‾ k H n ‾ k , \begin{aligned} \hat{\mathbf{x}}_{k} &=\rho \overline{\mathbf{W}}_{k}^{\mathrm{H}} \overline{\mathbf{H}}_{k} \overline{\mathbf{V}} \mathbf{x}+\overline{\mathbf{W}}_{k}^{\mathrm{H}} \overline{\mathbf{n}}_{k}, \quad \forall k \in\{1, \ldots, K\} \\ &=\rho \overline{\mathbf{W}}_{k}^{\mathrm{H}} \overline{\mathbf{H}}_{k} \overline{\mathbf{V}}_{k} \mathbf{x}_{k}+\sum_{j \neq k} \rho \overline{\mathbf{W}}_{k}^{\mathrm{H}} \overline{\mathbf{H}}_{k} \overline{\mathbf{V}}_{j} \mathbf{x}_{j}+\overline{\mathbf{W}}_{k}^{\mathrm{H}} \overline{\mathbf{n}}_{k}, \end{aligned} x^k=ρWkHHkVx+WkHnk,∀k∈{1,…,K}=ρWkHHkVkxk+j=k∑ρWkHHkVjxj+WkHnk,
其中, V ‾ ≜ [ V ‾ 1 … V ‾ K ] ∈ C M B S × L \overline{\mathbf{V}} \triangleq\left[\overline{\mathbf{V}}_{1} \ldots \overline{\mathbf{V}}_{K}\right] \in \mathbb{C}^{M_{\mathrm{BS}} \times L} V≜[V1…VK]∈CMBS×L表示归一化数据预编码器(数字)且 V ‾ k ≜ [ V ‾ k , 1 … V ‾ k , L k ] \overline{\mathbf{V}}_{k} \triangleq\left[\overline{\mathbf{V}}_{k}, 1 \ldots \overline{\mathbf{V}}_{k, L_{k}}\right] Vk≜[Vk,1…Vk,Lk]。注意: H ‾ k \overline{\mathbf{H}}_{k} Hk是经过GoB波束成形后的等效信道。 W ‾ k ∈ C M U E × L k \overline{\mathbf{W}}_{k} \in \mathbb{C}^{M_{\mathrm{UE}} \times L_{k}} Wk∈CMUE×Lk是第 k k k个用户的数据合并器(数字)。 n ‾ k ≜ W k H n k \overline{\mathbf{n}}_{k} \triangleq \mathbf{W}_{k}^{\mathrm{H}} \mathbf{n}_{k} nk≜WkHnk为第 k k k个用户的接收噪声。
第 k k k个用户的瞬时频谱效率可以表示为:
R k ( V , V ‾ , W , W ‾ ) \mathcal{R}_{k}(\mathbf{V}, \overline{\mathbf{V}}, \mathbf{W}, \overline{\mathbf{W}}) Rk(V,V,W,W)
≜ log 2 det ( I L k + ρ 2 K ‾ k − 1 W ‾ k H H ‾ k V ‾ k V ‾ k H H ‾ k H W ‾ k ) \quad \triangleq \log _{2} \operatorname{det}\left(\mathbf{I}_{L_{k}}+\rho^{2} \overline{\mathbf{K}}_{k}^{-1} \overline{\mathbf{W}}_{k}^{\mathrm{H}} \overline{\mathbf{H}}_{k} \overline{\mathbf{V}}_{k} \overline{\mathbf{V}}_{k}^{\mathrm{H}} \overline{\mathbf{H}}_{k}^{\mathrm{H}} \overline{\mathbf{W}}_{k}\right) ≜log2det(ILk+ρ2Kk−1WkHHkVkVkHHkHWk)
其中: K ‾ k ≜ ρ 2 ∑ j ≠ k W ‾ k H H ‾ k V ‾ j V ‾ j H H ‾ k H W ‾ k + σ n 2 W ‾ k H W k H W k W ‾ k \overline{\mathbf{K}}_{k} \triangleq \rho^{2} \sum_{j \neq k} \overline{\mathbf{W}}_{k}^{\mathrm{H}} \overline{\mathbf{H}}_{k} \overline{\mathbf{V}}_{j} \overline{\mathbf{V}}_{j}^{\mathrm{H}} \overline{\mathbf{H}}_{k}^{\mathrm{H}} \overline{\mathbf{W}}_{k}+\sigma_{n}^{2} \overline{\mathbf{W}}_{k}^{\mathrm{H}} \mathbf{W}_{k}^{\mathrm{H}} \mathbf{W}_{k} \overline{\mathbf{W}}_{k} Kk≜ρ2∑j=kWkHHkVjVjHHkHWk+σn2WkHWkHWkWk为第 k k k个用户有关的干扰加噪声协方差。
最优预编码器与合并器设计问题
为了最大化网络吞吐量,需要考虑最佳GoB(模拟,有约束)与最优数据波束成形(数字,无约束)。
这里首先定义训练开销:
V ∈ C N B S × M B S \mathbf{V} \in \mathbb{C}^{N_{\mathrm{BS}} \times M_{\mathrm{BS}}} V∈CNBS×MBS表示基站端的GoB预编码。训练开销 ω ( V ) ∈ [ 0 , 1 ] \omega(\mathbf{V}) \in[0,1] ω(V)∈[0,1]定义为:
ω ( V ) ≜ τ T card ( col ( V ) ) \omega(\mathbf{V}) \triangleq \frac{\tau}{T} \operatorname{card}(\operatorname{col}(\mathbf{V})) ω(V)≜Tτcard(col(V))
可以看出:训练开销大部分取决于GoB预编码器 V \mathbf{V} V的设计, V \mathbf{V} V实际上包含了信道估计阶段要训练的波束。
因此,可实现的有效网络吞吐量可以表示为:
R ( V , V ‾ , W , W ‾ ) ≜ ( 1 − ω ( V ) ) ∑ k = 1 K R k ( V , V ‾ , W , W ‾ ) \mathcal{R}(\mathbf{V}, \overline{\mathbf{V}}, \mathbf{W}, \overline{\mathbf{W}}) \triangleq(1-\omega(\mathbf{V})) \sum_{k=1}^{K} \mathcal{R}_{k}(\mathbf{V}, \overline{\mathbf{V}}, \mathbf{W}, \overline{\mathbf{W}}) R(V,V,W,W)≜(1−ω(V))k=1∑KRk(V,V,W,W)
整个优化问题可以表示为:
( V ∗ , V ‾ ∗ , W ∗ , W ‾ ∗ ) = argmax V , V ‾ , W , W ‾ E H [ R ( V , V ‾ , W , W ‾ ) ] subject to col ( V ) ∈ B B S col ( W k ) ∈ B U E , ∀ k = { 1 , … , K } . ( P ⋆ ) \begin{aligned} \left(\mathbf{V}^{*},\right.&\left.\overline{\mathbf{V}}^{*}, \mathbf{W}^{*}, \overline{\mathbf{W}}^{*}\right) =\underset{\mathbf{V}, \overline{\mathbf{V}}, \mathbf{W}, \overline{\mathbf{W}}}{\operatorname{argmax}} \mathbb{E}_{\mathbf{H}}[\mathcal{R}(\mathbf{V}, \overline{\mathbf{V}}, \mathbf{W}, \overline{\mathbf{W}})] \\& \text { subject to } \operatorname{col}(\mathbf{V}) \in \mathcal{B}_{\mathrm{BS}} \\ &\quad\quad\quad\quad\quad\operatorname{col}\left(\mathbf{W}_{k}\right) \in \mathcal{B}_{\mathrm{UE}}, \quad \forall k=\{1, \ldots, K\} .\qquad(\mathrm{P} \star) \end{aligned} (V∗,V∗,W∗,W∗)=V,V,W,WargmaxEH[R(V,V,W,W)] subject to col(V)∈BBScol(Wk)∈BUE,∀k={1,…,K}.(P⋆)
直接求解 ( P ⋆ ) (\mathrm{P} \star) (P⋆)是十分困难的,一个通用并且有效的方法是解耦设计。即:GoB波束成形可以使用长时间的统计信息来优化,mMIMO数据波束成形可以采用瞬时CSI来进行优化。具体来说,考虑两个时间不同的时间尺度:
- 小时间尺度(信道相干时间):在信道相干时间内,假设瞬时信道实现 H k , ∀ k \mathbf{H}_{k}, \forall k Hk,∀k是恒定的,只执行单一的训练阶段。
- 大时间尺度(波束相干时间):在波束相干时间内,假设协方差矩阵 Σ k , ∀ k \mathbf{\Sigma}_{k}, \forall k Σk,∀k是恒定的,GoB波束成形被设计(即:波束选择)。
数据波束成形设计
BD(Block Diagonalization, BD)预编码在处理多用户干扰方面已经被证明是一个渐进最优的波束成形方法。我们考虑在BS侧通过 V ‾ \overline{\mathbf{V}} V产生一个没有用户间干扰的块对角 H ‾ V ‾ \overline{\mathbf{H}} \overline{\mathbf{V}} HV,然后通过接收端的用户合并器来抑制流间干扰。BD预编码将允许根据长期的GoB波束成形来简化SE表达式。具体过程如下:满足块对角的 H ‾ V ‾ \overline{\mathbf{H}} \overline{\mathbf{V}} HV需要满足如下条件:
H ‾ j V ‾ k = 0 , ∀ j ≠ k \overline{\mathbf{H}}_{j} \overline{\mathbf{V}}_{k}=\mathbf{0}, \forall j \neq k HjVk=0,∀j=k
通过引入矩阵:
H ‾ / k ≜ [ H ‾ 1 T … H ‾ k − 1 T H ‾ k + 1 T … H ‾ K T ] T ∈ H ‾ / k ∈ C ( K − 1 ) M U E × M B S \overline{\mathbf{H}}_{/ k} \triangleq\left[\overline{\mathbf{H}}_{1}^{\mathrm{T}} \ldots \overline{\mathbf{H}}_{k-1}^{\mathrm{T}} \overline{\mathbf{H}}_{k+1}^{\mathrm{T}} \ldots \overline{\mathbf{H}}_{K}^{\mathrm{T}}\right]^{\mathrm{T}} \in \overline{\mathbf{H}}_{/ k} \in \mathbb{C}^{(K-1) M_{\mathrm{UE}} \times M_{\mathrm{BS}}} H/k≜[H1T…Hk−1THk+1T…HKT]T∈H/k∈C(K−1)MUE×MBS
然后将使得 V ‾ k \overline{\mathbf{V}}_{k} Vk位于 H ‾ / k \overline{\mathbf{H}}_{/ k} H/k的零空间即可。
首先,对 H ‾ / k \overline{\mathbf{H}}_{/ k} H/k执行奇异值分解(SVD),即:
H ‾ / k = U ‾ / k S ‾ / k [ M ‾ / k ( 1 ) M ‾ / k ( 0 ) ] H \overline{\mathbf{H}}_{/ k}=\overline{\mathbf{U}}_{/ k} \overline{\mathbf{S}}_{/ k}\left[\overline{\mathbf{M}}_{/ k}^{(1)} \overline{\mathbf{M}}_{/ k}^{(0)}\right]^{\mathrm{H}} H/k=U/kS/k[M/k(1)M/k(0)]H
其中, M ‾ / k ( 1 ) \overline{\mathbf{M}}_{/ k}^{(1)} M/k(1)为 H ‾ / k \overline{\mathbf{H}}_{/ k} H/k前 M ˉ / k ≜ rank ( H ‾ / k ) \bar{M}_{/ k} \triangleq \operatorname{rank}\left(\overline{\mathbf{H}}_{/ k}\right) Mˉ/k≜rank(H/k)大的右奇异值向量, M ‾ / k ( 0 ) \overline{\mathbf{M}}_{/ k}^{(0)} M/k(0)包含了剩下的 ( M B S − M ˉ / k ) \left(M_{\mathrm{BS}}-\bar{M}_{/ k}\right) (MBS−Mˉ/k),此时有:
H ‾ j M ‾ / k ( 0 ) = 0 , ∀ j ≠ k \overline{\mathbf{H}}_{j} \overline{\mathbf{M}}_{/ k}^{(0)}=\mathbf{0}, \quad \forall j \neq k HjM/k(0)=0,∀j=k
BD的整个多用户有效信道可以表示为:
H ‾ B D = [ H ‾ 1 M ‾ / 1 ( 0 ) 0 ⋱ 0 H ‾ K M ‾ / K ( 0 ) ] \overline{\mathbf{H}}_{\mathrm{BD}}=\left[\begin{array}{ccc} \overline{\mathbf{H}}_{1} \overline{\mathbf{M}}_{/ 1}^{(0)} & & \mathbf{0} \\ & \ddots & \\ \mathbf{0} & & \overline{\mathbf{H}}_{K} \overline{\mathbf{M}}_{/ K}^{(0)} \end{array}\right] HBD=⎣⎢⎡H1M/1(0)0⋱0HKM/K(0)⎦⎥⎤
由于 H ‾ B D \overline{\mathbf{H}}_{\mathrm{BD}} HBD是块对角的,再一次对每个块执行SVD分解有:
H ‾ k M ‾ / k ( 0 ) = [ U ‾ k ( 1 ) U ‾ k ( 0 ) ] [ S ‾ k 0 0 0 ] [ M ‾ k ( 1 ) M ‾ k ( 0 ) ] H \overline{\mathbf{H}}_{k} \overline{\mathbf{M}}_{/ k}^{(0)}=\left[\overline{\mathbf{U}}_{k}^{(1)} \overline{\mathbf{U}}_{k}^{(0)}\right]\left[\begin{array}{cc} \overline{\mathbf{S}}_{k} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array}\right]\left[\overline{\mathbf{M}}_{k}^{(1)} \overline{\mathbf{M}}_{k}^{(0)}\right]^{\mathrm{H}} HkM/k(0)=[Uk(1)Uk(0)][Sk000][Mk(1)Mk(0)]H
乘积项 M ‾ / k ( 0 ) M ‾ k ( 1 ) \overline{\mathbf{M}}_{/ k}^{(0)} \overline{\mathbf{M}}_{k}^{(1)} M/k(0)Mk(1)长生了一个维度为 L k ≜ rank ( H ‾ k M ‾ / k ( 0 ) ) L_{k} \triangleq \operatorname{rank}\left(\overline{\mathbf{H}}_{k} \overline{\mathbf{M}}_{/ k}^{(0)}\right) Lk≜rank(HkM/k(0))的正交基,它可以用来作为第 k k k个用户的多用户干扰归零的数据预编码器,即:
V ‾ k = M ‾ / k ( 0 ) M k ( 1 ) \overline{\mathbf{V}}_{k}=\overline{\mathbf{M}}_{/ k}^{(0)} \mathbf{M}_{k}^{(1)} Vk=M/k(0)Mk(1)
同样,第 k k k个用户相关的接收数据合并器可以设计为:
W ‾ k = U ‾ k ( 1 ) \overline{\mathbf{W}}_{k}=\overline{\mathbf{U}}_{k}^{(1)} Wk=Uk(1)
所有干扰消除的条件满足后,经过BD后瞬时频谱效率可以表示为:
R k B D ( V , W ) ≜ log 2 det ( I L k + κ S ‾ k H S ‾ k ) \mathcal{R}_{k}^{\mathrm{BD}}(\mathbf{V}, \mathbf{W}) \triangleq \log _{2} \operatorname{det}\left(\mathbf{I}_{L_{k}}+\kappa \overline{\mathbf{S}}_{k}^{\mathrm{H}} \overline{\mathbf{S}}_{k}\right) RkBD(V,W)≜log2det(ILk+κSkHSk)
其中, V \mathbf{V} V和 W \mathbf{W} W被隐藏在 H ‾ k M ‾ / k ( 0 ) \overline{\mathbf{H}}_{k} \overline{\mathbf{M}}_{/ k}^{(0)} HkM/k(0)的线性转换中(因为 H ‾ ≜ W H H V \overline{\mathbf{H}} \triangleq \mathbf{W}^{\mathrm{H}} \mathbf{H V} H≜WHHV)。
此时固定,固定设计好的数据波束成形器,一个基于长时间的联合收发端模拟波束选择问题可以表示为:
( V ( P 0 ) , W ( P 0 ) ) = argmax V , W E H [ ( 1 − ω ( V ) ) ∑ k = 1 K R k B D ( V , W ) ] subject to col ( V ) ∈ B B S col ( W k ) ∈ B U E , ∀ k = { 1 , … , K } . ( P 0 ) \begin{aligned} &\left(\mathbf{V}^{(\mathrm{P} 0)}, \mathbf{W}^{(\mathrm{P} 0)}\right) \\ &=\underset{\mathbf{V}, \mathbf{W}}{\operatorname{argmax}} \mathbb{E}_{\mathbf{H}}\left[(1-\omega(\mathbf{V})) \sum_{k=1}^{K} \mathcal{R}_{k}^{\mathrm{BD}}(\mathbf{V}, \mathbf{W})\right] \\ &\qquad\text { subject to } \operatorname{col}(\mathbf{V}) \in \mathcal{B}_{\mathrm{BS}} \\ & \\ &\qquad\operatorname{col}\left(\mathbf{W}_{k}\right) \in \mathcal{B}_{\mathrm{UE}}, \quad \forall k=\{1, \ldots, K\} . \quad(\mathrm{P} 0) \end{aligned} (V(P0),W(P0))=V,WargmaxEH[(1−ω(V))k=1∑KRkBD(V,W)] subject to col(V)∈BBScol(Wk)∈BUE,∀k={1,…,K}.(P0)
GoD波束成形设计
设计合适的GoB波束成形有三个意义:
- 获得较大的有效信道增益
- 避免灾难性的多用户干扰
- 尽量减少训练开销
下面将针对每种意义进行波束设计,并随之产生相关近似 ( P 0 ) (\mathrm{P} 0) (P0)的优化问题。
最大化有效信道增益
经典的GoB配置中,不考虑波束间的相关性,所有波束都被训练。这种方法只适用于小范围的GoB,但是随之而来有较大的性能损失。因此,为了避免这种性能换开销的问题,直觉是使用一个大的GoB,并利用长期统计信息的知识,训练几个选定的波束来训练,从而保持 ω = ( τ / T ) M B S \omega=(\tau / T) M_{\mathrm{BS}} ω=(τ/T)MBS小。(其实在毫米波单用户场景下,信道的稀疏性足够满足通过低维表示来代表信道)
定义: M k \mathcal{M}_{k} Mk表示包含了第 k k k个用户的相关信道成分(或相关波束对):
M k ≜ { ( v , w ) : E H k [ ∣ w w H H k v v ∣ 2 ] ≥ ξ } \mathcal{M}_{k} \triangleq\left\{(v, w): \mathbb{E}_{\mathbf{H}_{k}}\left[\left|\mathbf{w}_{w}^{\mathrm{H}} \mathbf{H}_{k} \mathbf{v}_{v}\right|^{2}\right] \geq \xi\right\} Mk≜{(v,w):EHk[∣∣wwHHkvv∣∣2]≥ξ}
其中, ξ \xi ξ是预先定义的功率阈值。
从UE的角度定义波束对集:
当第 k k k个UE采用自身的接收GoB合并器 W k \mathbf{W}_{k} Wk,定义 M k B S ⊆ M k \mathcal{M}_{k}^{\mathrm{BS}} \subseteq \mathcal{M}_{k} MkBS⊆Mk包含了相关的信道组件(即:波束对)如下:
M k B S ( W k ) ≜ { ( v , w ) ∈ M k : w w ∈ W k } \mathcal{M}_{k}^{\mathrm{BS}}\left(\mathbf{W}_{k}\right) \triangleq\left\{(v, w) \in \mathcal{M}_{k}: \mathbf{w}_{w} \in \mathbf{W}_{k}\right\} MkBS(Wk)≜{(v,w)∈Mk:ww∈Wk}
M k B S ( ⋅ ) \mathcal{M}_{k}^{B S}(\cdot) MkBS(⋅)强调集合 M k B S \mathcal{M}_{k}^{B S} MkBS取决于其选择的GoB合并器 W k \mathbf{W}_{k} Wk。
下面展示信道相关成分与信道二阶统计量(信道协方差矩阵)的关系。 Σ k ≜ E H k [ vec ( H k ) vec ( H k ) H ] ∈ C N B S N U E × N B S N U E \boldsymbol{\Sigma}_{k} \triangleq \mathbb{E}_{\mathbf{H}_{k}}\left[\operatorname{vec}\left(\mathbf{H}_{k}\right) \operatorname{vec}\left(\mathbf{H}_{k}\right)^{\mathrm{H}}\right] \in \mathbb{C}^{N_\mathrm{BS}N_{\mathrm{UE}} \times N_{\mathrm{BS}} N_{\mathrm{UE}}} Σk≜EHk[vec(Hk)vec(Hk)H]∈CNBSNUE×NBSNUE表示第 k k k个UE相关的信道协方差矩阵,则 M k \mathcal{M}_{k} Mk可以等效地表示为:
M k = { ( v , w ) : b v , w H Σ k b v , w ≥ ξ } \mathcal{M}_{k}=\left\{(v, w): \mathbf{b}_{v, w}^{\mathrm{H}} \boldsymbol{\Sigma}_{k} \mathbf{b}_{v, w} \geq \xi\right\} Mk={(v,w):bv,wHΣkbv,w≥ξ}
其中, b v , w ≜ ( conj ( v v ) ⊗ w w ) ∈ C N B S N U E × 1 \mathbf{b}_{v, w} \triangleq\left(\operatorname{conj}\left(\mathbf{v}_{v}\right) \otimes \mathbf{w}_{w}\right) \in \mathbb{C}^{N_{\mathrm{BS}} N_{\mathrm{UE}} \times 1} bv,w≜(conj(vv)⊗ww)∈CNBSNUE×1(证明略为简单,可参考原文)。
在已知 H k \mathbf{H}_{k} Hk二阶统计的情况下,相关的信道参数可以在 B B S B U E B_{\mathrm{BS}} B_{\mathrm{UE}} BBSBUE个元素上执行一个线性搜索获得。
同样地,如果考虑给定的GoB波束成形 V k ∈ C N B S × M B S \mathbf{V}_{k} \in \mathbb{C}^{N_{\mathrm{BS}} \times M_{\mathrm{BS}}} Vk∈CNBS×MBS和 W k ∈ C N U E × M L \mathbf{W}_{k} \in \mathbb{C}^{N_{\mathrm{UE}} \times M_{\mathrm{L}}} Wk∈CNUE×ML,则有效信道的协方差矩阵 Σ ˉ k \bar{\Sigma}_{k} Σˉk可以表示为:
Σ ‾ k = B k H Σ k B k \overline{\boldsymbol{\Sigma}}_{k}=\mathbf{B}_{k}^{\mathrm{H}} \boldsymbol{\Sigma}_{k} \mathbf{B}_{k} Σk=BkHΣkBk
其中 B k ≜ ( conj ( V k ) ⊗ W k ) ∈ C N B S N U E × M B S M U E \mathbf{B}_{k} \triangleq\left(\operatorname{conj}\left(\mathbf{V}_{k}\right) \otimes \mathbf{W}_{k}\right) \in \mathbb{C}^{N_{\mathrm{BS}} N_{\mathrm{UE}} \times M_{\mathrm{BS}} M_{\mathrm{UE}}} Bk≜(conj(Vk)⊗Wk)∈CNBSNUE×MBSMUE
这里,由于前面的BD将多用户之间的干扰解耦,所以作者考虑的是基于等效信道 H ‾ k ≜ W k H H k V k \overline{\mathbf{H}}_{k} \triangleq \mathbf{W}_{k}^{\mathrm{H}} \mathbf{H}_{k} \mathbf{V}_{k} Hk≜WkHHkVkSVD分解的SE:
R k S V D ( V k , W k ) ≜ log 2 det ( I M U E + κ Λ k H Λ k ) \mathcal{R}_{k}^{\mathrm{SVD}}\left(\mathbf{V}_{k}, \mathbf{W}_{k}\right) \triangleq \log _{2} \operatorname{det}\left(\mathbf{I}_{M_{\mathrm{UE}}}+\kappa \boldsymbol{\Lambda}_{k}^{\mathrm{H}} \boldsymbol{\Lambda}_{k}\right) RkSVD(Vk,Wk)≜log2det(IMUE+κΛkHΛk)
且其平均SE的上界为:
E H k [ R k SVD ( V k , W k ) ] ≤ M U E log 2 ( 1 + κ M U E − 1 Tr ( Σ ‾ k ) ) \mathbb{E}_{\mathbf{H}_{k}}\left[\mathcal{R}_{k}^{\text {SVD }}\left(\mathbf{V}_{k}, \mathbf{W}_{k}\right)\right] \leq M_{\mathrm{UE}} \log _{2}\left(1+\kappa M_{\mathrm{UE}}^{-1} \operatorname{Tr}\left(\overline{\boldsymbol{\Sigma}}_{k}\right)\right) EHk[RkSVD (Vk,Wk)]≤MUElog2(1+κMUE−1Tr(Σk))
而: Tr ( Σ ‾ k ) = Tr ( B k H Σ k B k ) = ∑ m = 1 M B S M U E b m H Σ k b m . \begin{aligned} \operatorname{Tr}\left(\overline{\boldsymbol{\Sigma}}_{k}\right) &=\operatorname{Tr}\left(\mathbf{B}_{k}^{\mathrm{H}} \boldsymbol{\Sigma}_{k} \mathbf{B}_{k}\right) \\ &=\sum_{m=1}^{M_{\mathrm{BS}} M_{\mathrm{UE}}} \mathbf{b}_{m}^{\mathrm{H}} \boldsymbol{\Sigma}_{k} \mathbf{b}_{m} . \end{aligned} Tr(Σk)=Tr(BkHΣkBk)=m=1∑MBSMUEbmHΣkbm.
因此,SE的上界可以通过合适的波束选择来对有有效信道协方差 Σ ˉ k \bar{\Sigma}_{k} Σˉk进行整形来最大化这个上界。即:在 M k \mathcal{M}_{k} Mk中选择前 M B S M U E M_{\mathrm{BS}} M_{\mathrm{UE}} MBSMUE大的信道相关成分对应的波束对。
因此, ( P 0 ) (\mathrm{P0}) (P0)被近似为如下的非协作的 ( P 1 ) (\mathrm{P1}) (P1)问题,其致力于优化 ∑ k = 1 K R k SVD ( V k , W k ) \sum_{k=1}^{K} \mathcal{R}_{k}^{\operatorname{SVD}}\left(\mathbf{V}_{k}, \mathbf{W}_{k}\right) ∑k=1KRkSVD(Vk,Wk)定义的总SE:
( V ( P 1 ) , W ( P 1 ) ) = argmax V , W ∑ k = 1 K M U E log 2 ( 1 + κ M U E − 1 Tr ( Σ ‾ k ) ) subject to col ( V ) ∈ B B S col ( W k ) ∈ B U E , ∀ k = { 1 , … , K } \begin{aligned} \left(\mathbf{V}^{(\mathrm{P} 1)}, \mathbf{W}^{(\mathrm{P} 1)}\right) \\ =\underset{\mathbf{V}, \mathbf{W}}{\operatorname{argmax}} & \sum_{k=1}^{K} M_{\mathrm{UE}} \log _{2}\left(1+\kappa M_{\mathrm{UE}}^{-1} \operatorname{Tr}\left(\overline{\boldsymbol{\Sigma}}_{k}\right)\right) \\ &\text { subject to } \operatorname{col}(\mathbf{V}) \in \mathcal{B}_{\mathrm{BS}} \\ & \operatorname{col}\left(\mathbf{W}_{k}\right) \in \mathcal{B}_{\mathrm{UE}}, \quad \forall k=\{1, \ldots, K\} \end{aligned} (V(P1),W(P1))=V,Wargmaxk=1∑KMUElog2(1+κMUE−1Tr(Σk)) subject to col(V)∈BBScol(Wk)∈BUE,∀k={1,…,K}
可以看出P1与用户解耦,每个UE可以单独解决目标和函数中和其相关的项。P1将作为后面算法的基线,在之前大多的HBF工作也是这样的非协作式HBF,其适用于FDD mMIMO。
最小化用户间干扰
使用BD的时,没有多用户间的两个关键关键条件:
- 无用户间干扰: ∣ null ( H ‾ / k ) ∣ ≠ 0 \left|\operatorname{null}\left(\overline{\mathbf{H}}_{/ k}\right)\right| \neq 0 ∣∣null(H/k)∣∣=0
- 无数据流间干扰: rank ( H ‾ k M ‾ / k ( 0 ) ) ≥ 1 \operatorname{rank}\left(\overline{\mathbf{H}}_{k} \overline{\mathbf{M}}_{/ k}^{(0)}\right) \geq 1 rank(HkM/k(0))≥1
第二个条件在FDD mMIMO几乎是满足的。而第一个条线满足的底线是 ( K − 1 ) M U E < M B S (K-1) M_{\mathrm{UE}}<M_{\mathrm{BS}} (K−1)MUE<MBS,它也是BD预编码对GoB波束设计施加抑制多用户干扰的唯一条件。
BD的使用会影响接收增益,这种影响取决于等效信道 H ‾ ≜ W H H V \overline{\mathbf{H}} \triangleq \mathbf{W}^{\mathrm{H}} \mathbf{H V} H≜WHHV的空间分离度。空间分离度越低性能损失越大。可以使用的相关矩阵距离(CMD)推断这种损失。CMD被用于增加UE间的空间可分离性,其是通过UE侧的协方差整形实现的。对于多用户,引入广义CMD(GCMD)。以第 k k k个UE为例子,其与第 j j j个UE的信道协方差之间的GCMD,GCMD的定义如下:
δ k ( Σ 1 , … , Σ K ) ≜ 1 − 1 K − 1 ∑ j = 1 K Tr ( Σ k Σ j ) ∥ Σ k ∥ F ∥ Σ j ∥ F \delta_{k}\left(\Sigma_{1}, \ldots, \Sigma_{K}\right) \triangleq 1-\frac{1}{K-1} \sum_{j=1}^{K} \frac{\operatorname{Tr}\left(\Sigma_{k} \Sigma_{j}\right)}{\left\|\Sigma_{k}\right\|_{\mathrm{F}}\left\|\Sigma_{j}\right\|_{\mathrm{F}}} δk(Σ1,…,ΣK)≜1−K−11j=1∑K∥Σk∥F∥Σj∥FTr(ΣkΣj)
两种比较极端的情况:
- 用户空间正交时: Tr ( Σ k Σ j ) = 0 , ∀ j ≠ k \operatorname{Tr}\left(\Sigma_{k} \Sigma_{j}\right)=0, \quad \forall j \neq k Tr(ΣkΣj)=0,∀j=k,此时 δ k ( Σ 1 , … , Σ K ) = 1 , ∀ k \delta_{k}\left(\Sigma_{1}, \ldots, \Sigma_{K}\right)=1, \quad \forall k δk(Σ1,…,ΣK)=1,∀k。
- 用户完全不可空间分离:用户间协方差矩阵彼此差一个比例因子(即:完全不可空间分离), δ k ( Σ 1 , … , Σ K ) = 0 , ∀ k \delta_{k}\left(\Sigma_{1}, \ldots, \Sigma_{K}\right)=0, \quad \forall k δk(Σ1,…,ΣK)=0,∀k。
当信道协方差通过GoB波束成形进行塑形,产生一些有效的信道协方差时,GCMD可以作为衡量协方差形成如何影响UEs空间可分性的指标。
考虑用GCMD度量BDprecoding之后的有效协方差, Σ ˉ k ≜ B k H Σ k B k , ∀ k \bar{\Sigma}_{k} \triangleq \mathbf{B}_{k}^{\mathrm{H}} \Sigma_{k} \mathbf{B}_{k}, \quad \forall k Σˉk≜BkHΣkBk,∀k,其中 B k ≜ ( conj ( V ) ⊗ W k ) \mathbf{B}_{k} \triangleq(\operatorname{conj}(\mathbf{V}) \otimes\left.\mathbf{W}_{k}\right) Bk≜(conj(V)⊗Wk)。引入GCMD作为 R k SVD ( V k , W k ) \mathcal{R}_{k}^{\operatorname{SVD}}\left(\mathbf{V}_{k}, \mathbf{W}_{k}\right) RkSVD(Vk,Wk)的一个惩罚因子,此时的设计因为可以表示为:
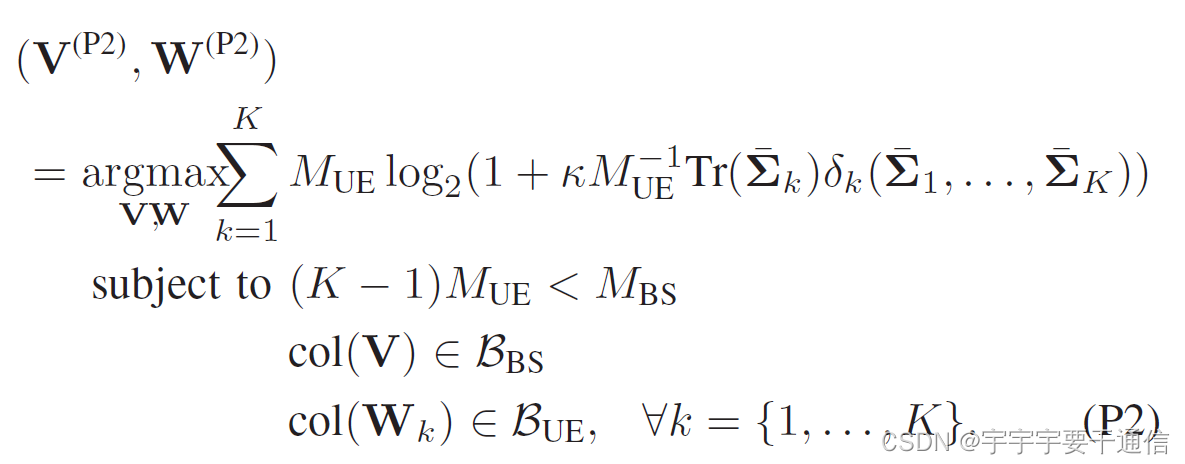
不难发现,P2需要一个中央协调器知道所有的大维度信道协方差,它规定了每个UE的波束策略
最小化训练开销
前面两种策略忽略了训练开销,现在研究FDD mMIMO系统中有效的GoB波束成形设计所需的第三个条件:即训练开销的最小化。
之前的训练开销 ω ( V ) \omega(\mathbf{V}) ω(V)其范围为: [ 1 , ( τ / T ) B B S ] \left[1,(\tau / T) B_{\mathrm{BS}}\right] [1,(τ/T)BBS]。(右边的极值当所有波束被训练时即可取到。)
另一种替代的方案是,考虑训练器相关的信道组件(等价于,波束对),此时 V \mathbf{V} V和 W \mathbf{W} W的设计不是分离的。(这种考虑其实也更符合实际,在当前的3GPP规范中。设计了一个波束报告程序,以协助BS选择预编码器,这样的程序直接影响下行SE的表现。PMI(Precoding Matrix Indicator)就是这样的操作,UE根据适当的GoB合并器(波束)选择报告给BS集合 M k B S ( W k ) \mathcal{M}_{k}^{\mathrm{BS}}\left(\mathbf{W}_{k}\right) MkBS(Wk))。因此,根据在UE侧进行的波束决定,重新定义了训练开销:
ω ( W ) ≜ τ T card ( ⋃ k = 1 K M k B S ( W k ) ) \omega(\mathbf{W}) \triangleq \frac{\tau}{T} \operatorname{card}\left(\bigcup_{k=1}^{K} \mathcal{M}_{k}^{\mathrm{BS}}\left(\mathbf{W}_{k}\right)\right) ω(W)≜Tτcard(⋃k=1KMkBS(Wk))
其中, W ∈ C K N U E × K M U E \mathbf{W} \in \mathbb{C}^{K N_{\mathrm{UE}} \times K M_{\mathrm{UE}}} W∈CKNUE×KMUE是所有用户的合并器。
因此,在3GPP协议中,在GoB的方法下,每个UE进行的波束决策非常影响训练开销。随着传播环境中散射逐渐丰富,训练开销会极大地增长,甚至接近极值 ( τ / T ) B B S (\tau / T) B_{\mathrm{BS}} (τ/T)BBS。采用诸如(P1)或(P2)等方法选择波束可能会破坏GoB方法在多用户场景中的应用。
考虑训练开销的减少也有利于BS处尽可能少地激活波束,因此实际中考虑,训练开销和波束成形增益的trade-off是有意义的。
因此,在目标函数的log项前面加一个修正因子,以考虑训练开销和可实现的信道增益,具体问题如下:
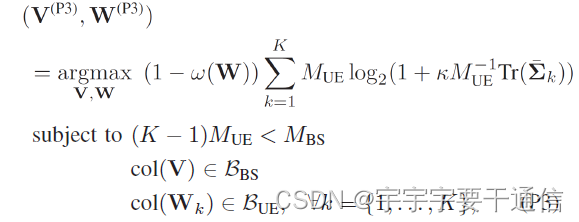
综上,考虑三个条件:信道增益、用户间干扰、训练开销,得到一个终极版本:
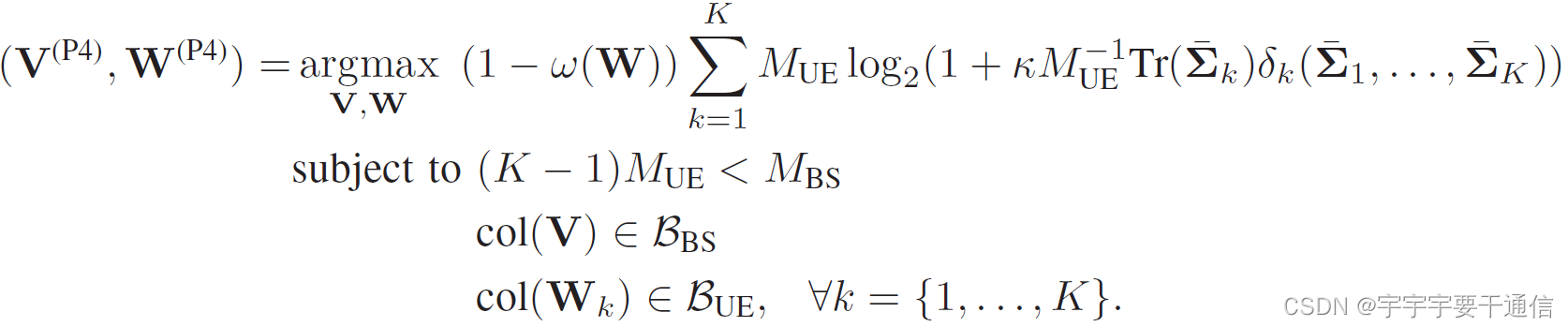
对这四个优化问题,总结如下表:

文章给出了,P4,相较于其他问题,也是原始问题P0最紧的上界。
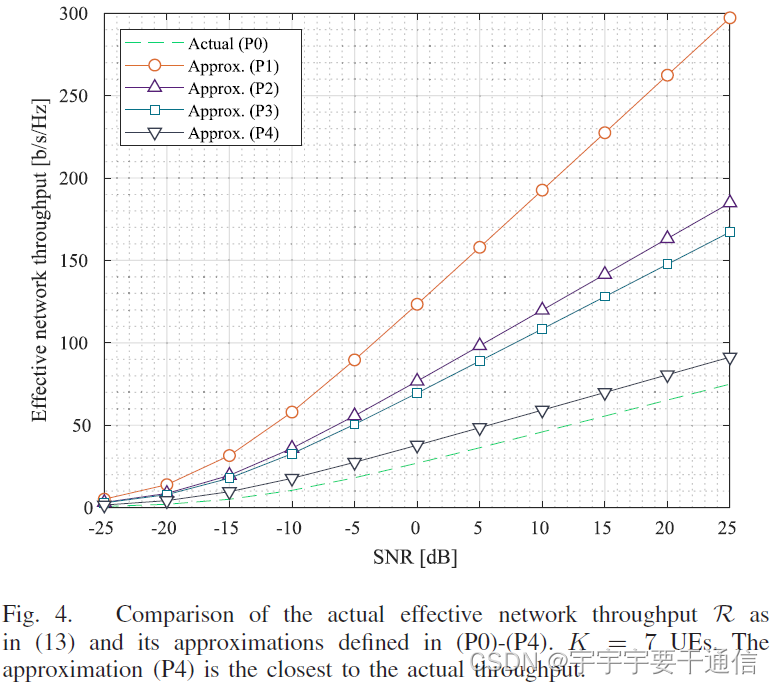
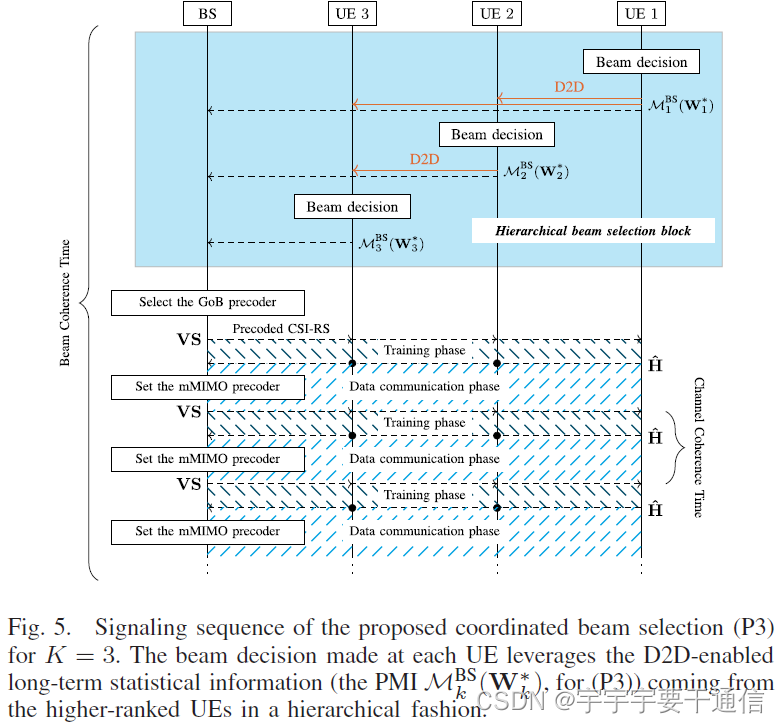
去中心化的协同波束选择算法
为了实现去中心化的协同,考虑一种需要较小开销的分层信息结构。即:在各UE之间建立了一个(任意的)顺序,第 k k k个终端可以访问(排名较低的)终端的一些长期统计信息
1 、 … … k − 1 1、……k−1 1、……k−1。这种配置在D2D通信中可以实现,实际上在3GPP的R16中预计将支持点对点侧链接,其更容易以较低的资源开销支持UE间的协作通信。
下表总结了不同问题,在第 k k k个用户所需要的信息:

从上图可以看出,P1-P3都可以看成是P4的一个特例,所以我们关注P4的求解。
定义集合 W k − 1 ≜ { W 1 ∗ , … , W k − 1 ∗ } \mathcal{W}_{k-1} \triangleq\left\{\mathbf{W}_{1}^{*}, \ldots, \mathbf{W}_{k-1}^{*}\right\} Wk−1≜{W1∗,…,Wk−1∗}包含了前 k k k步已经固定的波束决策。根据分层架构,第 k k k个用户知道集合 B f i x ( W k − 1 ) ≜ ∪ j = 1 k − 1 M j B S ( W j ∗ ) \mathcal{B}^{\mathrm{fix}}\left(\mathcal{W}_{k-1}\right) \triangleq \cup_{j=1}^{k-1} \mathcal{M}_{j}^{\mathrm{BS}}\left(\mathbf{W}_{j}^{*}\right) Bfix(Wk−1)≜∪j=1k−1MjBS(Wj∗)和有效信道协方差 Σ ˉ j , ∀ j ∈ { 1 , … , k − 1 } \bar{\Sigma}_{j}, \forall j \in\{1, \ldots, k-1\} Σˉj,∀j∈{1,…,k−1}。因此,对于第 k k k个用户:
- 计算部分GCMD δ k ( Σ ‾ 1 , … , Σ ‾ k ) \delta_{k}\left(\overline{\boldsymbol{\Sigma}}_{1}, \ldots, \overline{\boldsymbol{\Sigma}}_{k}\right) δk(Σ1,…,Σk)
- 构建一个与 B f i x ( W k − 1 ) \mathcal{B}^{\mathrm{fix}}\left(\mathcal{W}_{k-1}\right) Bfix(Wk−1)相关的部分GoB预编码 V k − 1 \mathbf{V}_{k-1} Vk−1,即: col ( V k − 1 ) = { v v ∈ B B S : ( v , w ) ∈ B f i x ( W k − 1 ) } \operatorname{col}\left(\mathbf{V}_{k-1}\right)=\left\{\mathbf{v}_{v} \in \mathcal{B}_{\mathrm{BS}}:(v, w) \in\right.\left.\mathcal{B}^{\mathrm{fix}}\left(\mathcal{W}_{k-1}\right)\right\} col(Vk−1)={vv∈BBS:(v,w)∈Bfix(Wk−1)}。同样地,第 k k k个UE可以计算一个部分 ω ( W k − 1 ) \omega\left(\mathcal{W}_{k-1}\right) ω(Wk−1)。
最后,第 k k k个UE的去中心化波束决策 W k ∗ \mathbf{W}_{k}^{*} Wk∗可以递归表示如下:
W k ∗ = argmax W k f k ( [ V k V k − 1 ] , { W k , W k − 1 } ) , \mathbf{W}_{k}^{*}=\underset{\mathbf{W}_{k}}{\operatorname{argmax}} f_{k}\left(\left[\mathbf{V}_{k} \mathbf{V}_{k-1}\right],\left\{\mathbf{W}_{k}, \mathcal{W}_{k-1}\right\}\right), Wk∗=Wkargmaxfk([VkVk−1],{Wk,Wk−1}),
其中, col ( V k ) = { v v ∈ B B S : ( v , w ) ∈ M k B S ( W k ) } \operatorname{col}\left(\mathbf{V}_{k}\right)=\left\{\mathbf{v}_{v} \in \mathcal{B}_{\mathrm{BS}}:(v, w) \in \mathcal{M}_{k}^{\mathrm{BS}}\left(\mathbf{W}_{k}\right)\right\} col(Vk)={vv∈BBS:(v,w)∈MkBS(Wk)}, f k ( V , W ) f_{k}(\mathbf{V}, \mathcal{W}) fk(V,W)定义如下:
f k ( V , W ) ≜ { M U E log 2 ( 1 + κ M U E − 1 Tr ( Σ ‾ k ) δ k ( Σ ˉ 1 , … , Σ ˉ k ) ) ( 1 − ω ( W ) ) M U E log 2 ( 1 + κ M U E − 1 Tr ( Σ ˉ k ) ) ( 1 − ω ( W ) ) M U E log 2 ( 1 + κ M U E − 1 Tr ( Σ ˉ k ) δ k ( Σ ˉ 1 , … , Σ ˉ k ) ) f_{k}(\mathbf{V}, \mathcal{W}) \triangleq\left\{\begin{array}{l} M_{\mathrm{UE}} \log _{2}\left(1+\kappa M_{\mathrm{UE}}^{-1} \operatorname{Tr}\left(\overline{\boldsymbol{\Sigma}}_{k}\right) \delta_{k}\left(\bar{\Sigma}_{1}, \ldots, \bar{\Sigma}_{k}\right)\right) \\ (1-\omega(\mathcal{W})) M_{\mathrm{UE}} \log _{2}\left(1+\kappa M_{\mathrm{UE}}^{-1} \operatorname{Tr}\left(\bar{\Sigma}_{k}\right)\right) \\ (1-\omega(\mathcal{W})) M_{\mathrm{UE}} \log _{2}\left(1+\kappa M_{\mathrm{UE}}^{-1} \operatorname{Tr}\left(\bar{\Sigma}_{k}\right) \delta_{k}\left(\bar{\Sigma}_{1}, \ldots, \bar{\Sigma}_{k}\right)\right) \end{array}\right. fk(V,W)≜⎩⎨⎧MUElog2(1+κMUE−1Tr(Σk)δk(Σˉ1,…,Σˉk))(1−ω(W))MUElog2(1+κMUE−1Tr(Σˉk))(1−ω(W))MUElog2(1+κMUE−1Tr(Σˉk)δk(Σˉ1,…,Σˉk))
该方案背后的直觉是让第 k k k个UE选择 W k ∈ B U E \mathbf{W}_{k} \in \mathcal{B}_{\mathrm{UE}} Wk∈BUE,以贪婪的方式最大化其各自的目标函数中和的第k项。
仿真结果分析
仿真场景参数:
- N B S = 64 N_{\mathrm{BS}}=64 NBS=64, N U E = 4 N_{\mathrm{UE}}=4 NUE=4
-
- B B S \mathcal{B}_{\mathrm{BS}} BBS和 B U E \mathcal{B}_{\mathrm{UE}} BUE中的波束成形向量设置为基于3GPP-NR码本的DFT正交波束。
- 假设允许UE向BS分别指示最多4个相关的波束对,即: M k B S ( W k ∗ ) \mathcal{M}_{k}^{\mathrm{BS}}\left(\mathbf{W}_{k}^{*}\right) MkBS(Wk∗)被限制为它4个最强的元素。(这相当于NR的第二类CSI报告)
- UE使用MMSE的方法估计其瞬时信道。然后反馈给BS进行基于BD的预编码器设计。Zadoff-Chu序列被用于训练有效信道。
上述的流程如下:
- 仿真考虑在相邻的25个RB上进行(每个RB包含12个子载波和14个OFDM符号),总共带宽为5MHz,总共的RE为(141225)/ T coh T_\text{coh} Tcoh
- 信道模型设置为Winner II,
仿真结果
对比基线设置为相应的TDD模式下(在完全信道互易性假设下,BD预编码后得到了TDD设置的曲线。即:预编码器直接应用于全维 K N U E × N B S KN_{\mathrm{UE}} \times N_{\mathrm{BS}} KNUE×NBS信道,而FDD则是基于有效信道传输,使用GoB预编码),考虑理想和非理想CSI。
吞吐量 v.s. SNR
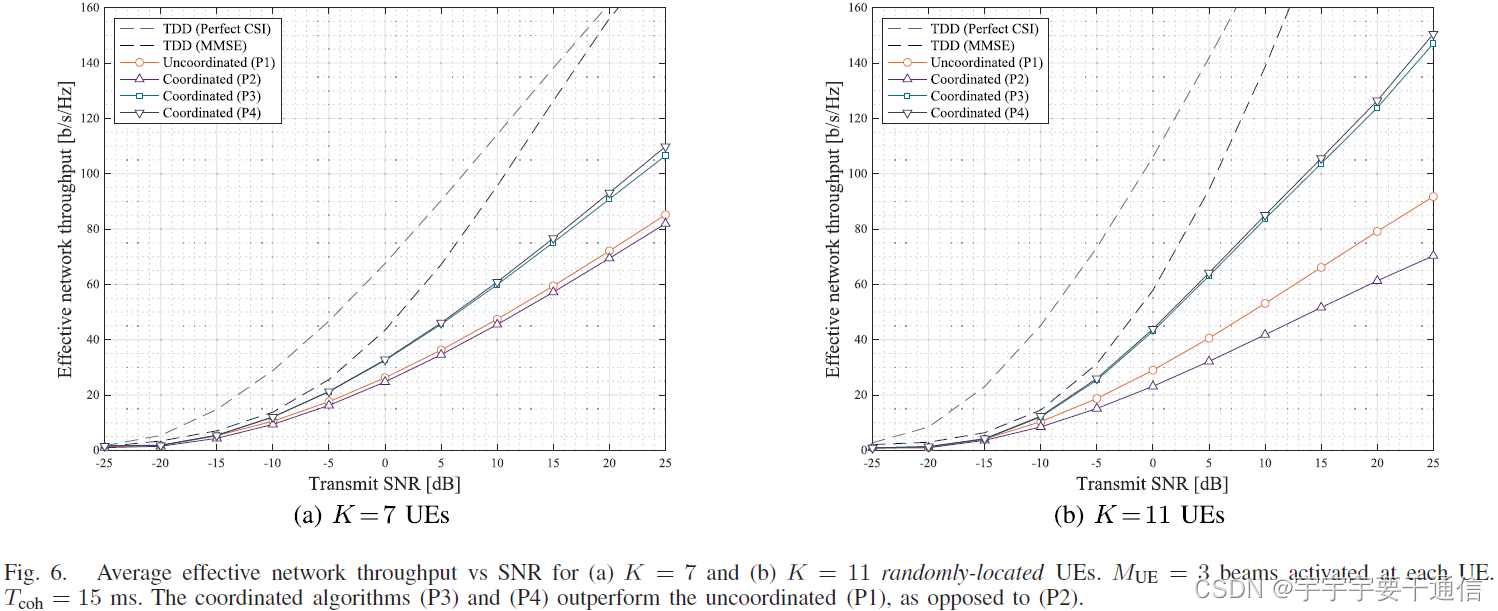
图6a展示7个UE, T c o h = 15 m s T_{\mathrm{coh}}=15 \mathrm{~ms} Tcoh=15 ms下的吞吐量。结论如下:
- TDD实现了比FDD更好的吞吐量
- P3,P4比无协作的P1性能好,
- 由于 T c o h T_{\mathrm{coh}} Tcoh较小,log前因子占主导,所以P3和P4性能接近。(此时,P3更适合实际场景,因为P3要求的信息更少)
- P2性能比P1差,特别是当信道相干时间 T c o h T_{\mathrm{coh}} Tcoh较小时,通过塑造协方差来最大化UE的空间可分性是反效果的.
- 训练开销随着 K K K增加,因此,图6b中用户数 K = 11 K=11 K=11,算法(P3)和(P4)的性能增益更大,同样,(P2)和(P1)差距更大!
相对增益 v.s.信道相关时间
图7展示了 K = 7 UEs K=7\text{UEs} K=7UEs,以及 K = 11 UEs K=11\text{UEs} K=11UEs时,相较于无协作波束选择的吞吐量v.s.信道相关时间,而图8展示的是激活的波束数量。
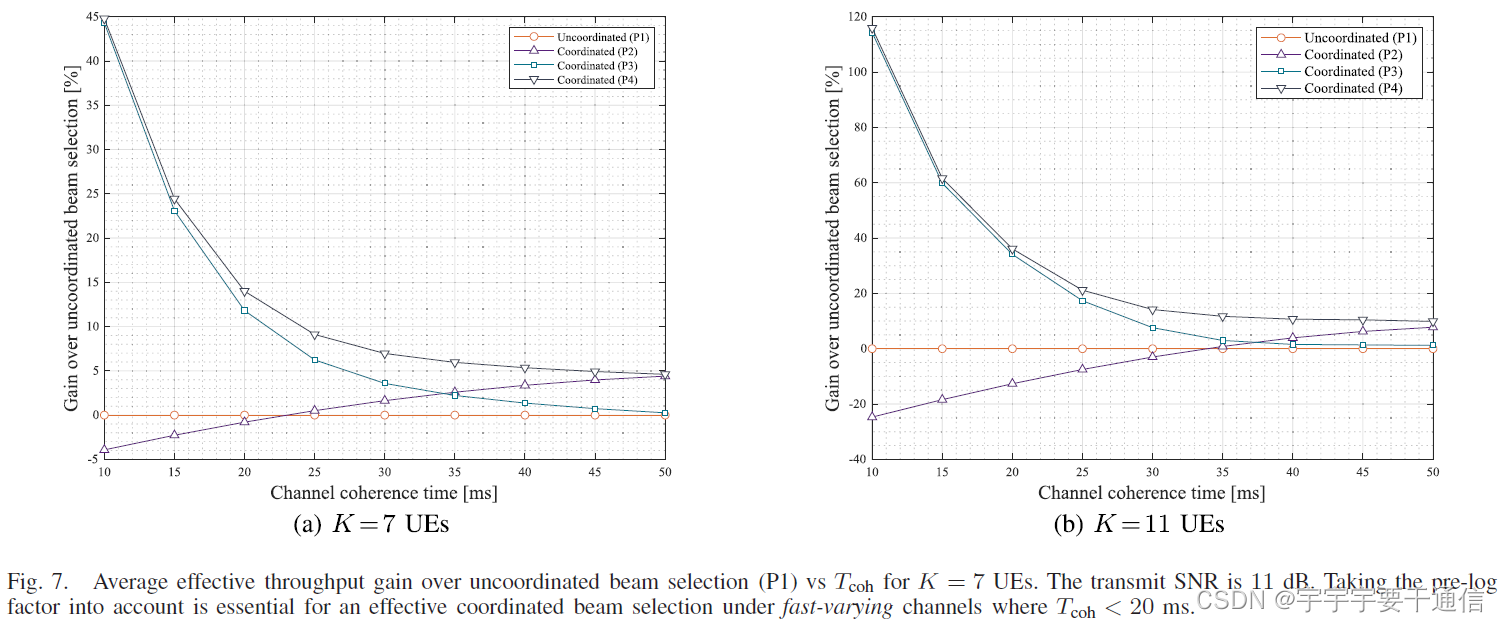
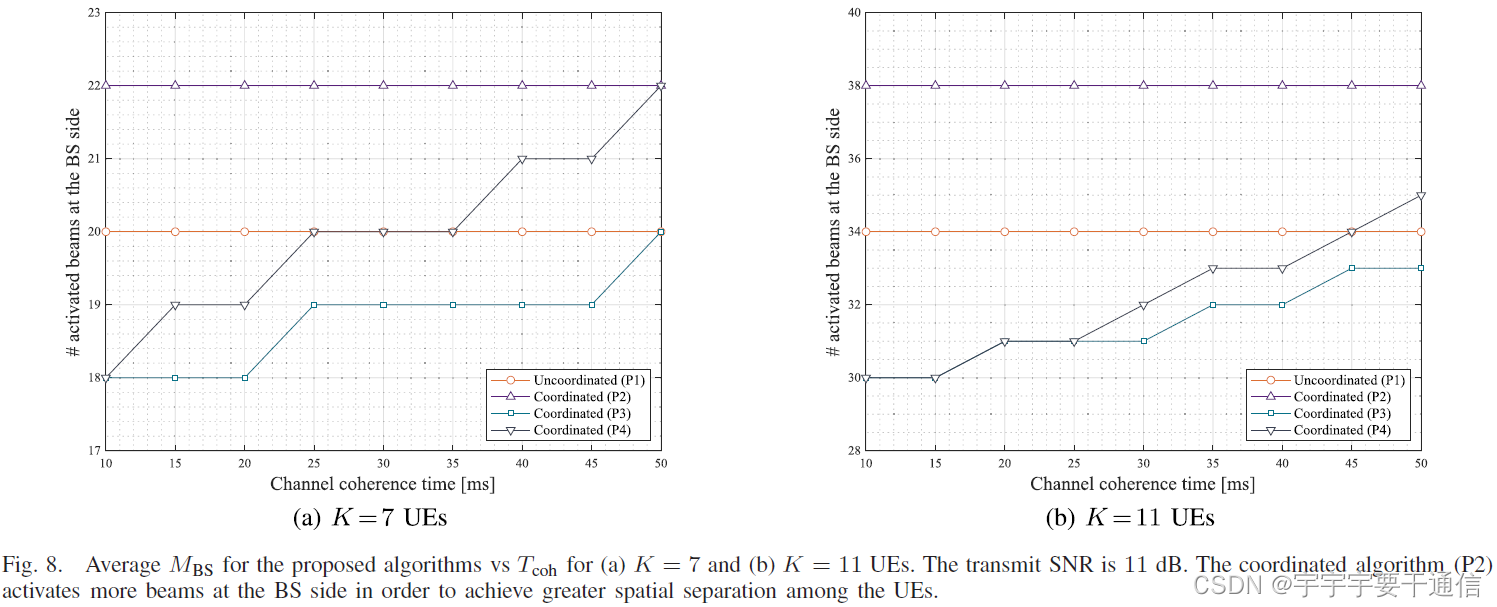
- T c o h < 20 m s T_{\mathrm{coh}}<20 \mathrm{~ms} Tcoh<20 ms,车辆或快速行人通道:(P3)和(P4)相较于其他方案有更高的增益,(P2)性能不及无协作的(P1)。而在图8中确实可以看到为了实现更高的空间可分离性,(P2)在BS端激活了更多数目的波束,这在快速变化的信道中是有害的。
- T c o h ≥ 20 m s T_{\mathrm{coh}} \geq 20 \mathrm{~ms} Tcoh≥20 ms,步行信道:(P3)(P4)与(P1)的性能差距减小。(P3)收敛于(P1),这是因为对于长信道相干时间,训练开销可以忽略不计,更重要的是关注log因子。,同样地原因,(P2)性能优于(P1)。(P4)收敛于(P2),因此对于较长的通道相干时间,根据表二,(P2)可以避免一些额外的协调开销,是可取的。 图8中,增加用户数,这些现象更加明显。
下面还考虑一种特殊情况:UE相关性更高。
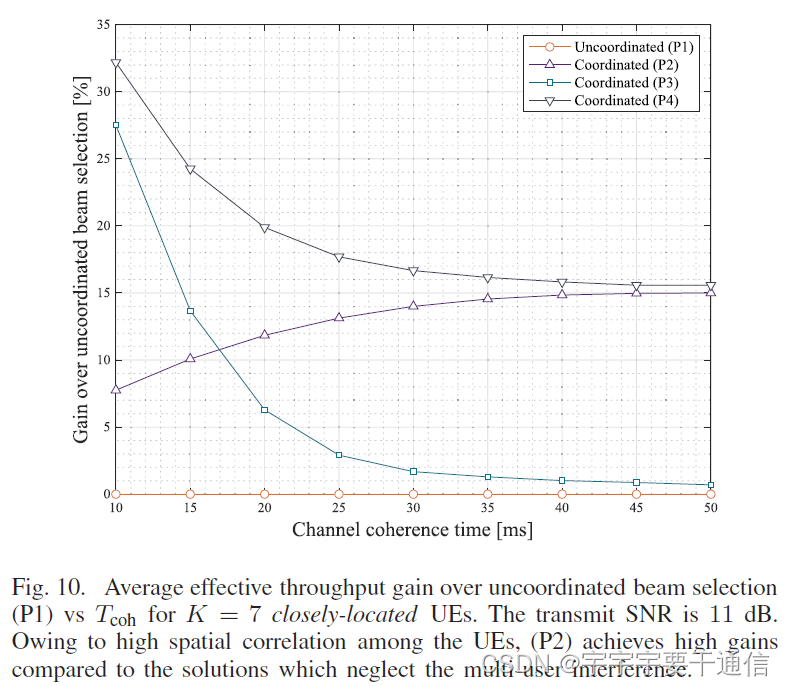
可以看出,(P2)相较于不考虑多用户干扰的方案实现了更高的性能。即使是在小于20ms的相干时间内,多用户干扰也是不可忽略的因素。(P4)获得的性能提高更需要交换一些额外的长期信息。
吞吐量 v.s. 反馈量化比特
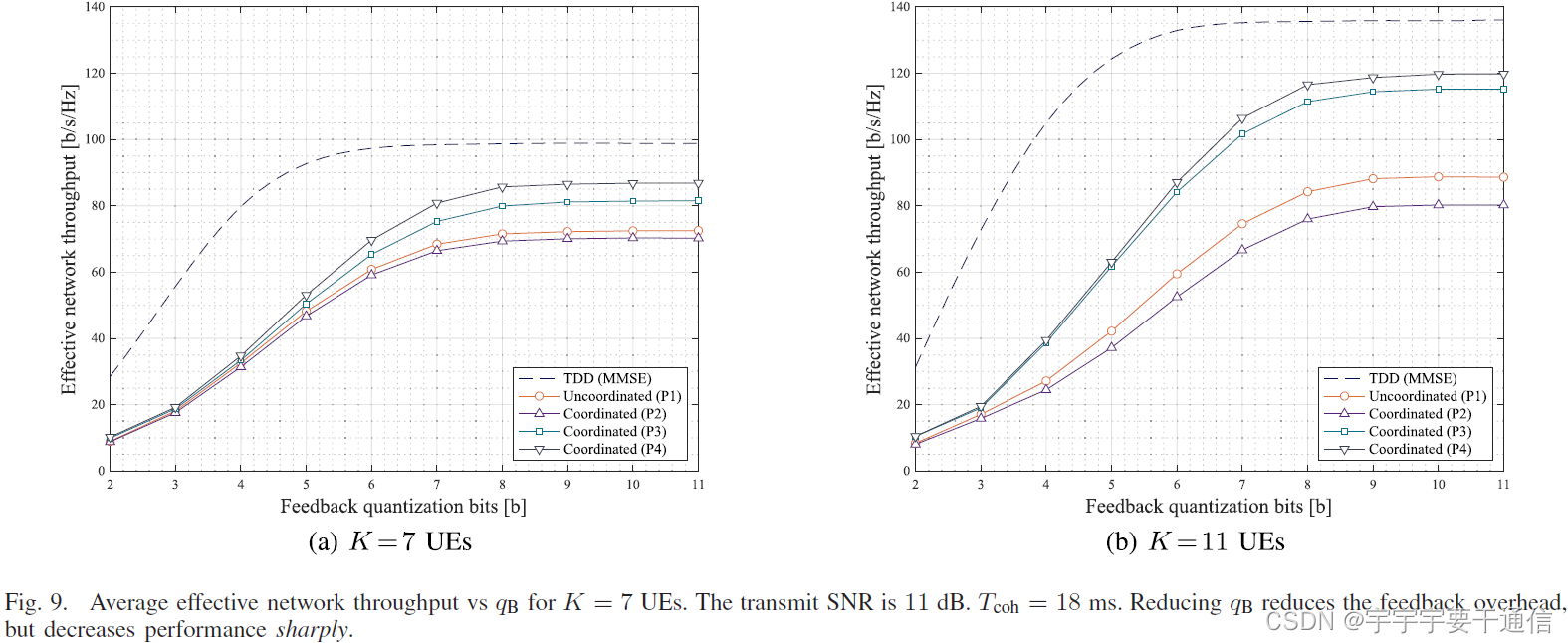
考虑信道估计使用均匀量化(逐元素量化),此时设置 SNR = 11 d B , T coh = 18 ms \text{SNR}=11dB,T_\text{coh}=18\text{ms} SNR=11dB,Tcoh=18ms结论如下:
- 降低量化比特数 q B q\text{B} qB导致吞吐量大幅下降,对于FDD制式下,是从 q B ≤ 7 q\text{B}\leq7 qB≤7开始的。
- q B ≤ 7 q\text{B}\leq7 qB≤7越小,各算法之间的性能差距同时也减小。
- q B ≤ 7 q\text{B}\leq7 qB≤7越小越有利减少上行频段的反馈开销。因此,反馈开销和协助通信获得的性能之间需要平衡。
摘记不易…但此文章给实际的工程部署提供了许多有价值的参考
这篇关于FDD-MU-mMIMO下针对快速波束训练的用户协同的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






