本文主要是介绍22《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》中文分享,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》
本人能力有限,如果错误欢迎批评指正。
第五章:Folding and Aggregation Are Cooperative Transitions
(折叠和聚合是同时进行的)
-蛋白质折叠的协同作用来自于二级和三级的结构相互作用
现在,我们应该如何理解在一个更复杂的过程中的协作性,比如蛋白质折叠?小的蛋白质被发现可以进行双态协同折叠,也就是说,蛋白质折叠过程中的中间产物的数量可以忽略不计。螺旋-线团理论现在以及不足以解释蛋白质的折叠协同性。因为β-折叠蛋白质也具有折叠协同性。此外,折叠蛋白质中的大多数螺旋都是短的,但螺旋-线团理论认为,短肽不应该形成稳定的螺旋。那么,我们错过了什么?
蛋白质折叠理论本身也不足以解释蛋白质内折叠的协同性。蛋白质中的疏水残基导致蛋白质在水中成为一个紧凑的结构,而这个过程是非常突然的。然而,晶格模型研究表明,聚合物这种压缩导致非协同转变,而不是协同转变。第3章的图3.9显示,6肽的 HP模型在变性转变的中点有大量的中间结构。这种协同性的缺乏并不是因为6- mer链太短,更长的链也经历了非协同的结构致密。
所以,如果我们不能单独用螺旋-线团过程或单独用结构致密来解释蛋白质折叠的双态性质,那又如何解释它呢?折叠协同作用似乎是由于二级和三级相互作用的组合。当两个螺旋在蛋白质折叠过程中形成时,每个螺旋本身都会形成一定的协同作用,但是,除此之外,两个螺旋相邻的排列有助于进一步稳定双螺旋配对。蛋白质螺旋通常是两亲性的,这意味着它的一边有一条疏水残基的条纹。当这些二级结构聚集在一起时,相邻螺旋的疏水条纹通常会相互面对。
为了说明二级结构之间的三级相互作用如何促进稳定性和协同性,我们重点关注螺旋束蛋白。在天然螺旋束蛋白中,多个螺旋(通常是三个或更多)就像一束棒状体并排排列。随着螺旋的协同形成,它们被捆绑在一起,从而提供更大的稳定性。螺旋会帮助其他螺旋的形成。这里有一个简单的模型来说明这个理论。
螺旋-螺旋之间的相互作用有助于螺旋-束蛋白的折叠协同性
首先,让我们模拟一个双螺旋束组装。然后,我们将模拟一个三螺旋束蛋白。这个双螺旋链有N个单体。图5.10 显示了我们的双螺旋模型中最重要的构象。我们将链的构象分为以下几个类:(i)线团状态(coil):整个链条完全变性,无结构。(ii)单螺旋状态(Single-helix):该链类似于谢尔曼:它可以是一个在任何地方、任何长度的单一螺旋延伸(高达最大的N个残基长)。为了使数学计算简单,我们将每个螺旋回合近似算为有4个氨基酸残基(而不是α螺旋中每转3.6个)。iii)两个相邻的螺旋被压缩起来,但只有部分( Two adjacent helices are zipped up, but only partially )。链有两个螺旋。这两个螺旋有完全相同的数字m = 1,2,3,…,的螺旋转弯。我们忽略了不匹配的螺旋长度或在错误位置的螺旋,因为它们的数量小得多。连接两个螺旋的是一个线圈状的环状结构。(所以,我们必须有M<N/2。)每条链的非螺旋部分都处于线团状态。(iv)原生状态( Native state):两个相邻的螺旋被完全压缩在一起,m = M。

图5.10对双螺旋束构象的分类。(A)单螺旋-线团的三种状态:无螺旋(即随机线团)、部分压缩的螺旋和完全压缩的螺旋。(B)双螺旋束状态的两种状态:部分形成的螺旋有m = 1,2,3,的转弯结构,或天然完全形成的双螺旋束,每个螺旋有m==M转弯。
现在,我们想计算出各种蛋白质构象的数量。让我们来构造这些状态的统计权重。值得注意的是,我们也同时考虑了只有线团以及只有螺旋结构的状态,如图5.10左侧的构象集合所示。这些构象的配分函数为Q1,当链的长度为N是,结合5.14可得出这个结论。其次,让我们计算一下双螺旋束状态,如图5.10的右侧所示。若双螺旋束的压缩状态为m,统计权重为

这里,σ2解释了两个螺旋的成核,s是每个螺旋旋转形成的统计权重(总共8m=(每个螺旋转角结构的4个单体)×(2个螺旋)×每个螺旋的m个转弯)。r(> 1)是一个平衡常数,它表示相邻螺旋之间的每个m个直接接触会产生多少额外的稳定性。螺旋-螺旋接触通常是疏水和结合相互作用导致的。公式5.20是对单螺旋链的公式5.13的对应物。
不同长度为m的双螺旋束构象(对应于公式5.14)对整体配分函数的贡献是
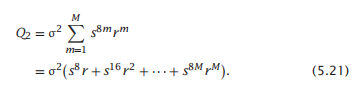
计算这些状态的总体,将该特定状态的统计权重放在分子中,并将和Q2hb = Q1+ Q2放在分母中。例如,p (2) = σ2s16r2/(Q1 + Q2)。然后,您可以计算平均值,例如双螺旋束的平均长度。
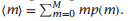
我们可以r来表示形成螺旋-螺旋接触相互作用的自由能εhh。

当没有螺旋-螺旋相互作用时,εhh = 0,导致r = 1。当螺旋-螺旋相互作用稳定时,εhh < 0,你有r > 1;这被称为正协同。在这个模型中,蛋白质折叠的协同作用可以来自螺旋-线团贡献(用σ和s表示)和螺旋-螺旋结构的吸引,由r > 1表达。
接下来我们要开始使用这个双螺旋束模型。我们有了N(如果整个链是螺旋,可以形成的最大氢键数);σ和s(螺旋-线团成核和增殖参数);r(每个有利的螺旋-螺旋相互作用的平衡常数);M,当蛋白质处于双螺旋束状态时,最大长度螺旋的氨基酸数量。然后,你计算配分函数Q2hb,模型中感兴趣的状态的总体,以及平均值和方差。Box 5.3 展示了如何使用已经计算过的Q1和Q2来处理三螺旋束蛋白质。
====================================================
Box 5.3 三螺旋束蛋白
使用与之前相同的逻辑,我们可以模拟一个三螺旋束蛋白质的折叠。假设主要的三螺旋束状态是那些三个螺旋中的每个螺旋都有相同的螺旋转弯数,m。假设螺旋完全相邻,则存在3m成对的螺旋-螺旋接触:在螺旋1-2、2-3和1-3之间。同样,取σ作为每个螺旋的成核常数,s作为增殖平衡常数,r作为成对的螺旋-螺旋平衡常数。在这个简单的模型中,三螺旋束状态的配分函数将是
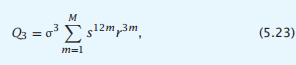
其中,M(< N/3)是原生结构中每个螺旋的最大转弯数。为了计算三螺旋束蛋白的任何状态的总体,我们将感兴趣的状态的统计权重放到分子中,并将和Q1 + 3Q2 + Q3放到分母中。图5.11显示了这种简化的模型如何捕捉由温度和尿素诱导的三螺旋束中的折叠-展开协同性。
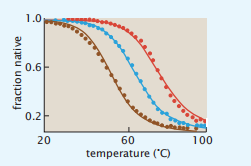
图5.11三螺旋束模型说明了温度和尿素的变性。三种浓度的尿素:2.0M(棕色)、1.5M(蓝色)和1.0M(红色)。
====================================================
总之,在小蛋白质折叠过程中观察到的可忽略的中间态种群可以解释为两种协同作用的产物:单个螺旋-线团过程具有协同性,螺旋-螺旋结构的堆积的相互作用进一步稳定结构。螺旋压缩因子s与螺旋-螺旋相互作用因子r结合,使双螺旋束状态比任何部分压缩或部分压缩状态更稳定。无论何时r > 1,这意味着螺旋-螺旋相互作用有助于稳定束状态。在这个模型中,三螺旋束比双螺旋束更稳定,因为在三螺旋束中有r3的因子,而在双螺旋束中只有r的因子。
这个模型已经相当简化了。首先,我们在这里只列举了“主导态”,而不是所有可能的构象。可以包括一些额外的构象,但是会导致额外的数学复杂性。我们模拟双螺旋状态时,我们只考虑那些螺旋完美地排列在一起的状态,因为rm因子显示非结合的螺旋对将会更少。我们还忽略了允许在序列的非原生位置上有双螺旋束状态形成的组合因子,因为这些项很小。像这样的简单模型的目的是捕捉一般的规律,而不是细节的内容。
-------------------------------------------
欢迎点赞收藏转发!
下次见!
这篇关于22《Protein Actions Principles and Modeling》-《蛋白质作用原理和建模》中文分享的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




