本文主要是介绍头疼的算法与数据结构——单链表详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
一、链表简介
1.基本信息
链表是一种常见的数据结构，不同于数组，在内存中是连续的一段内存空间，，虽然是一种线性表但是不会按照线性顺序去存储数据的数据结构，而是在每一个节点里存到下一个节点的指针(Pointer）。由于不必按顺序存储，链表在插入的时候可以达到O⑴的复杂度，比另一种线性表：顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n）的时间，而顺序表相应的时间复杂度分别是O(logn）和O⑴。使用链表结构可以克服数组链表需要预先知道数据大小的缺点，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。但是链表失去了数组随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大。在计算机科学中，链表作为一种基础的数据结构可以用来生成其它类型的数据结构。链表通常由一连串节点组成，每个节点包含任意的实例数据（data fields）和一或两个用来指向上一个/或下一个节点的位置的链接（links）。链表最明显的好处就是，常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序，数据的存取往往要在不同的排列顺序中转换。而链表是一种自我指示数据类型，因为它包含指向另一个相同类型的数据的指针（链接）。链表允许插入和移除表上任意位置上的节点，但是不允许随机存取。链表有很多种不同的类型：单向链#表，双向链表以及循环链表。链表可以在多种编程语言中实现。像Lisp和Scheme这样的语言的内建数据类型中就包含了链表的存取和操作。程序语言或面向对象语言，如C,C 和Java依靠易变工具来生成链表。
2.特点
数组的缺点在链表上就是优点，链表的确定就是数组的优点，合理利用这两种数据结构会让你的程序变得简单。
线性表的链式存储表示的特点是用一组任意的存储单元存储线性表的数据元素（这组存储单元可以是连续的，也可以是不连续的）。因此，为了表示每个数据元素 与其直接后继数据元素 之间的逻辑关系，对数据元素 来说，除了存储其本身的信息之外，还需存储一个指示其直接后继的信息（即直接后继的存储位置）。由这两部分信息组成一个结点（如概述旁的图所示），表示线性表中一个数据元素。线性表的链式存储表示，有一个缺点就是要找一个数，必须要从头开始找起，十分麻烦。
二、链表图解（linked List）
下图就是最简单最一般的单向链表：
还有这种：
多一个Tail指针，好处就是能很方便地找到末尾。
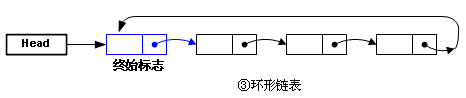
留一个终始标志，这个节点作为一个标志，不用于存储数据，链表末尾指向这个节点，形成一个“环形链表”，这样无论在链表的哪里插入新的元素，操作都一致了，不必判断头和尾的特殊性。
数组的好处就是链表的坏处，数组的坏处就是链表的好处，链表插入删除方便，遍历麻烦；数组遍历方便，插入删除都要移动。
因为需要从头开始找，没办法像数组那样直接跳到那个地址。而插入元素，就比数组方便了，如果你已经得知了要插入的地址的话，不过还要注意哦，是“后插入”（Insert After）：
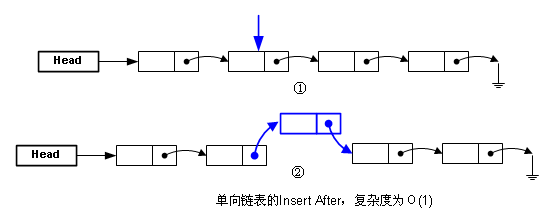
有“后插入”，那就有“前插入”（Insert Before），两者对单向链表来说真的不一样，下图描述了“前插入”：
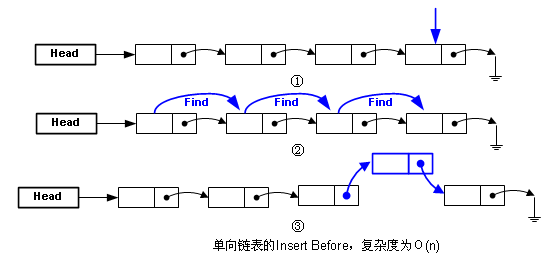
由于指针向后不向前，我们不知道要插入位置的前一个节点是什么，只能从头找，所以比较麻烦。
三、单链表的基本操作
今天先实现单链表的功能：
#include <stdio.h>struct node{int data;struct node *next;
};
typedef struct node Node;
#define SIZE sizeof(Node)//创建节点
Node* creteNode(int d)
{Node* pn=malloc(SIZE);pn->data=d;pn->next=NULL;return pn;
}//创建链表
void creatList(Node** h)
{Node* pn=NULL;Node* p=NULL;int d;printf("请输入数据\n");scanf("%d",&d);pn=creteNode(d);*h=pn;p=*h;while(1){printf("请输入数据\n");scanf("%d",&d);if(d==0)break;pn=creteNode(d);p->next=pn;p=p->next;}
} 这就是上面函数创建的
createNode函数创建一个个的节点，createList将一个个节点串起来。
//查找某个节点的位置
Node* findNode(Node* h,int n)
{int i;if((h==NULL)||(n<0)){printf("查找位置不合法||链表为空！\n");return NULL;}if(n==1){return h;}for(i=1;i<=n;i++){h=h->next;if(h==NULL)break;}return h;
}
//末尾增加一个新的节点
int addBack(int d,Node* h)
{Node *pn=NULL;pn=creteNode(d);Node* p=h;while(p->next){p=p->next;}p->next=pn;pn->next=NULL;
}
在末尾插入一个节点，先要遍历到最后一个节点，然后将新节点放在后面。
//头插法
int addFont(int d,Node** h)//修改头节点 传入二级指针
{Node* pn=NULL;pn=creteNode(d);pn->next=*h;*h=pn;
}
//插入
int insertNode(int n,int d,Node** h)//在n位置插入d
{if((n<1)||(*h==NULL)){printf("插入位置不合法||链表为空!\n");return 0;}Node* pn=creteNode(d);//创建新的节点//插入位置为1，即插入头节点的位置if(n==1){Node* pn=NULL;pn=creteNode(d);pn->next=*h;*h=pn;return 0;}else{Node* pf=findNode(h,n-1); //得到插入位置的前一个节点pn->next=pf->next;pf->next=pn;return 1;}
}
首先我们用findNode函数找到插入位置的前一个节点，插入的时候要记得先要断开以前的连接，删除也是的，先要断开连接再进行操作。
//删除第n个位置的元素
int deleteNode(int n,Node** h)
{//判断头节点是否为空，位置是不是合法if((*h==NULL)||(n<1)){printf("删除的链表为空||删除的位置不合法！\n");return 0;}Node* pd=NULL;//判断是否只有一个头节点if(((*h)->next)==NULL){printf("只用一个节点\n");return 0;}//删除头节点if(n==1){pd=*h;*h=pd->next;free(pd);pd=NULL;return 1;}//删除//判断节点是否存在if(NULL==findNode(*h,n-1)){printf("删除节点不存在\n");return 0;}//找到要删除的节点的前一个节点Node* pf=findNode(*h,n-1);pd=pf->next;//将要删除的节点的给pdpf->next=pd->next;free(pd);pd=NULL;pf=NULL;return 1;
}
也是用findNode函数找到前一个节点的位置，然后先断开删除节点位置和后面一个节点的位置。
//打印链表
void print(Node* h)
{printf("list:\n");while(h){printf("%d ",h->data);h=h->next;}printf("\n");
}int main()
{Node* head=NULL;creatList(&head);print(head);Node* p=findNode(head,0);printf("%d\n",p->data);deleteNode(2,&head);print(head);return 0;
}
这篇关于头疼的算法与数据结构——单链表详解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
