A - Area 51 Gym - 101334A 计算几何 极坐标 poj 1696 极坐标排序

本文主要是介绍A - Area 51 Gym - 101334A 计算几何 极坐标 poj 1696 极坐标排序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题意：

给定n个位于第一和第二象限的点，每一个点都有一个符号表示

给出一个序列，问从x轴的哪些区间从做往右看刚好符合这个序列

题解：

输入后进行极坐标排序，以负无穷为源点，按角的大小降序排列，若有相同角的就按照近的在前

再计算区间的分割点

然后枚举区间，看是否符合题意

这里不需要在枚举区间的时候都进行极坐标排序，只需要经过一个区间分割点的时候将两个字母换一个位置即可

#include<vector>
#include<math.h>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;vector<pair<double,double> >ans;#define MAXN 110
#define inf 0x3f3f3f3f
const double eps=1e-8;
char str[MAXN];
int now[MAXN*MAXN];
struct Point
{char ch[5];double x,y;Point(){}Point(double _X, double _Y){x = _X; y = _Y;}
};
Point P[MAXN];
struct Line
{double x;int t1,t2;Line(){}Line(double _x,int _t1,int _t2){x=_x,t1=_t1,t2=_t2;}
};
Line line[MAXN*MAXN];double Cross(Point p1,Point p2,Point p3){return (p2.x-p1.x)*(p3.y-p1.y)-(p2.y-p1.y)*(p3.x-p1.x);
}
double Dis(Point A, Point B){return sqrt((A.x-B.x)*(A.x-B.x) + (A.y-B.y)*(A.y-B.y));
}
Point operator - (Point A,Point B){return Point(A.x-B.x, A.y-B.y);
}
Point operator + (Point A, Point B){return Point(A.x+B.x, A.y+B.y);
}
Point operator * (Point A, double p){return Point(A.x*p, A.y*p);
}
bool operator == (Point A, Point B){return (A.x-B.x) == 0 && (A.y-B.y) == 0;
}
int sgn(double x)
{if(fabs(x)<eps)return 0;if(x<0)return -1;return 1;
}bool cmp(Point a, Point b)///按极角降序排序，若角度相等距离小的在前面
{return a.y!=b.y?a.y>b.y:a.x<b.x;
}bool cmpt(Line a,Line b)
{if(fabs(a.x-b.x)>eps) return a.x<b.x;if(a.t1!=b.t1)        return a.t1<b.t1;return a.t2<b.t2;
}double deal(int i,int j)
{double x1=P[i].x,y1=P[i].y;double x2=P[j].x,y2=P[j].y;if(x1==x2)return x1;return x1-y1/(y2-y1)*(x2-x1);
}bool check(int n)
{for(int i=0;i<n;i++)if(str[now[i]]!=P[i].ch[0])return 0;return 1;
}int main()
{int n;//freopen("in.txt","r",stdin);freopen("area.in","r",stdin);freopen("area.out","w",stdout);while(scanf("%d",&n)!=EOF){scanf("%s",str);for(int i=0;i<n;i++)scanf("%s%lf%lf",P[i].ch,&P[i].x,&P[i].y);sort(P,P+n,cmp);int cnt=0;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){if(P[i].y!=P[j].y){line[cnt].x=deal(i,j);line[cnt].t1=i;line[cnt++].t2=j;}}}line[cnt++]=Line(inf,0,0);sort(line,line+cnt,cmpt);for(int i=0;i<n;i++)now[i]=i;ans.clear();double last=-inf;for(int i=0;i<cnt;i++){if(last<line[i].x-eps&&check(n))ans.push_back(make_pair(last,line[i].x));last=line[i].x;swap(now[line[i].t1],now[line[i].t2]);}printf("%d\n",ans.size());for(int i=0;i<ans.size();i++){double x=ans[i].first,y=ans[i].second;x==-inf?printf("* "):printf("%0.8lf ",x);y==inf?printf("*"):printf("%0.8lf",y);printf("%c",i==ans.size()-1?'\n':' ');}}return 0;
}

Description

The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations:

1. It can not turn right due to its special body structure.
   
2. It leaves a red path while walking.
   
3. It hates to pass over a previously red colored path, and never does that.

The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.

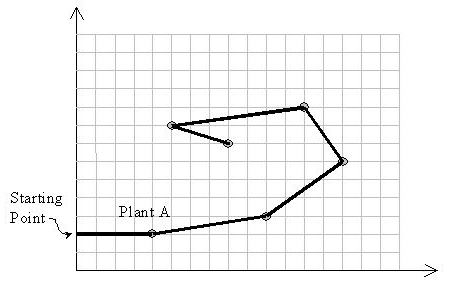
Input

Output

Sample Input

2
10
1 4 5
2 9 8
3 5 9
4 1 7
5 3 2
6 6 3
7 10 10
8 8 1
9 2 4
10 7 6
14
1 6 11
2 11 9
3 8 7
4 12 8
5 9 20
6 3 2
7 1 6
8 2 13
9 15 1
10 14 17
11 13 19
12 5 18
13 7 3
14 10 16

Sample Output

10 8 7 3 4 9 5 6 2 1 10
14 9 10 11 5 12 8 7 6 13 4 14 1 3 2

给出一些点，然后要你卷包裹一样卷起了，看图就能懂了

然后就是注意这里有一些点在同一条直线上

附下列代码

#include<math.h>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;const double eps = 1e-8;
int sgn(int x)
{if(abs(x) < eps)return 0;if(x < 0)return -1;else return 1;
}struct point
{int pos;int x,y;point(){}point(int _x,int _y){x=_x,y=_y;}
};
point p[100];double Dis(point p1,point p2){return sqrt((p1.x-p2.x)*(p1.x-p2.x)*1.0+1.0*(p1.y-p2.y)*(p1.y-p2.y));
}
double Cross(point p1,point p2,point p3){return (p2.x-p1.x)*(p3.y-p1.y)-(p2.y-p1.y)*(p3.x-p1.x);
}
point operator - (point A,point B){return point(A.x-B.x, A.y-B.y);
}
point operator + (point A, point B){return point(A.x+B.x, A.y+B.y);
}
point operator * (point A, double p){return point(A.x*p, A.y*p);
}
bool operator == (point A, point B){return (A.x-B.x) == 0 && (A.y-B.y) == 0;
}int pos;
bool cmp(point a,point b)
{double tmp =Cross(a,b,p[pos]);if(sgn(tmp) == 0)return Dis(p[pos],a) < Dis(p[pos],b);else if(sgn(tmp) < 0)return false;else return true;
}int main()
{int n,T;//freopen("in.txt","r",stdin);scanf("%d",&T);while(T--){scanf("%d",&n);scanf("%d%d%d",&p[0].pos,&p[0].x,&p[0].y);for(int i=1;i<n;i++){scanf("%d%d%d",&p[i].pos,&p[i].x,&p[i].y);if(p[i].y<p[0].y||p[i].y==p[0].y&&p[i].x<p[0].x)swap(p[0],p[i]);}pos=0;for(int i=1;i<n;i++){sort(p+i,p+n,cmp);pos++;}printf("%d",n);for(int i=0;i<n;i++)printf(" %d",p[i].pos);puts("");}return 0;
}

这篇关于A - Area 51 Gym - 101334A 计算几何 极坐标 poj 1696 极坐标排序的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！