案例系列：客户流失预测_构建建模_FeatureTools

介绍：建模

机器学习流程的最后一步也是价值所在。在我们开发了带有各自截止时间的标签之后，我们需要训练一个模型，将特征映射到预测标签。

在这个笔记本中，我们将使用特征矩阵和标签时间来训练和测试一个机器学习模型。我们将解决一个单一的预测问题，即在每个月的第一天预测哪些客户在该月内会流失，其中流失被定义为超过31天没有活跃会员资格，提前一个月的前导时间和一个月的预测窗口。

建模的一般过程如下所示：

方法

我们的基本机器学习方法是：

1. 为机器学习准备数据
   • 使用中位数插补填充缺失值
   • 对分类值进行编码
2. 根据时间将数据分为训练集和保留测试集
3. 评估基线逻辑回归模型
   • 为了比较，也尝试一个朴素的基准模型
4. 尝试一个非线性更强大的分类器，随机森林
   • 使用大部分默认超参数
   • 在保留测试数据上进行评估
5. 检查预测结果以确定是否满足业务需求
   • 使用精确度-召回率曲线来调整阈值
   • 使用混淆矩阵评估预测结果
   • 确定业务价值
6. 使用自动机器学习库自动优化模型
   • 使用TPOT，尽管有很多选择

最终的结果是一个经过优化的模型，可以解决预测给定参数下的客户流失的业务问题。该模型可以部署-用于对新数据进行预测。

# 导入必要的库
import os
import pandas as pd
import numpy as np# 忽略警告信息
import warnings
warnings.simplefilter('ignore')# 获取当前工作目录
CWD = os.getcwd()# 设置分区目录路径
PARTITION_DIR = f'{CWD}/data/partitions/'

# 读取p7文件夹下的MS-31_feature_matrix.csv文件，并将其存储在p7_fm变量中
p7_fm = pd.read_csv(f'{PARTITION_DIR}/p7/MS-31_feature_matrix.csv')# 显示p7_fm的前几行数据
p7_fm.head()

检索数据

通常情况下，对于这样大小的问题，所有的数据都会存储在AWS S3中，但是为了这个示例，我们将数据存储在本地。我们将检索之前笔记本中创建的20个特征矩阵的分区。对于这个问题，我们将使用一个提前量为1个月的导引偏移，这意味着我们的预测提前一个月进行。调整这个值会显著影响性能，因为模型更难学习到与特征的结束时间（由截止时间确定）更远的有意义的关系。

# 定义函数retrieve_data，参数为partition_num和label_type，默认值为'MS-31'
def retrieve_data(partition_num, label_type='MS-31'):"""Retrieve features and labels and merge. Lead periods is the number of offsets"""# 读取特征和标签数据fm = pd.read_csv(f'{PARTITION_DIR}/p{partition_num}/{label_type}_feature_matrix.csv', low_memory=False).\drop(columns=['label', 'days_to_churn', 'churn_date']) # 读取特征数据，去除label、days_to_churn和churn_date列labels = pd.read_csv(f'{PARTITION_DIR}/p{partition_num}/{label_type}_labels.csv', low_memory=False) # 读取标签数据# 合并特征和标签数据feature_matrix = fm.merge(labels, on=['msno', 'time'], how='inner').sort_values(['msno', 'time']) # 按照'msno'和'time'列进行内连接合并，并按照'msno'和'time'列排序return feature_matrix # 返回合并后的特征和标签数据

# 调用retrieve_data函数，获取数据
fm = retrieve_data(5)# 显示数据的前几行
fm.head()

下一个单元格检索了一些用于训练和测试的特征矩阵。

# 设置训练和测试特征矩阵的数量
fms_to_get = 20# 从磁盘中获取特征矩阵
fms = []
for i, r in enumerate(range(fms_to_get)):fm = retrieve_data(r)  # 调用retrieve_data函数获取特征矩阵print(f'{round(100 * (i / fms_to_get), 2)}% complete.', end='\r')  # 打印进度fms.append(fm)  # 将获取到的特征矩阵添加到列表中# 将特征矩阵合并并删除未知标签的行
feature_matrix = pd.concat(fms)  # 将特征矩阵列表合并为一个特征矩阵
feature_matrix = feature_matrix[~feature_matrix['label'].isna()].sort_values(['msno', 'time'])  # 删除标签未知的行，并按'msno'和'time'排序# 删除没有先前交易的行
feature_matrix = feature_matrix[~feature_matrix['TIME_SINCE_LAST(transactions.transaction_date)'].isna(
)]  # 删除'TIME_SINCE_LAST(transactions.transaction_date)'为空的行feature_matrix.shape  # 返回特征矩阵的形状

95.0% complete.

下面的单元格将布尔类型转换为整数，以在机器学习模型中使用。大多数布尔类型指示客户的所有值是否都为True（“All”原始值），或者日期是否为周末（“IsWeekend”原始值）。

# 将特征矩阵中的False替换为0，True替换为1
feature_matrix = feature_matrix.replace({False: 0, True: 1})

# 复制特征矩阵
feature_matrix_original = feature_matrix.copy()# 删除特征矩阵中的指定列
feature_matrix.drop(columns=[c for c in ['churn', 'days_to_next_churn', 'churn_date'] if c in feature_matrix], inplace=True)# 获取特征矩阵中包含'ALL'或者包含'WEEKEND'但不包含'PERCENT_TRUE'的布尔类型列
bool_cols = [c for c in feature_matrix if 'ALL' in c or ('WEEKEND' in c and 'PERCENT_TRUE' not in c)]# 将布尔类型列转换为浮点类型
for c in bool_cols:feature_matrix[c] = feature_matrix[c].astype(float)# 打印转换后的布尔类型列的前几行
feature_matrix[bool_cols].head()

# 删除特征矩阵中'msno'和'time'列的重复行，并将结果赋值给feature_matrix
feature_matrix = feature_matrix.drop_duplicates(subset=['msno', 'time'])

数据清洗

我们将进行一些基本的数据清洗步骤：

• 删除具有许多缺失值的列
• 删除具有单个唯一值的列
• 删除高度相关的 - 共线性 - 列

缺失值

我们将删除超过90%缺失值的列。

# 计算缺失值的百分比
missing_pct = feature_matrix.isnull().sum() / len(feature_matrix)# 找出缺失值比例大于0.9的特征，并将其转换为列表
to_drop = list((missing_pct[missing_pct > 0.9]).index)# 从to_drop列表中移除'days_to_churn'特征
to_drop = [x for x in to_drop if x != 'days_to_churn']# 返回to_drop列表
to_drop

# 删除指定的列
feature_matrix.drop(columns=to_drop, inplace=True)
# 返回删除指定列后的特征矩阵的形状
feature_matrix.shape

一个唯一值

只包含一个唯一值的列不包含任何信息，因此可以删除。

# 对特征矩阵进行操作，使用lambda函数判断每列的唯一值数量是否为1
one_unique = feature_matrix.apply(lambda x: x.nunique() == 1, axis=0)# 获取唯一值数量为1的列的索引，并将其转换为列表
to_drop = list(one_unique[one_unique == True].index)# 返回结果
to_drop

# 删除指定的列
feature_matrix.drop(columns=to_drop, inplace=True)# 返回删除指定列后的特征矩阵的形状
feature_matrix.shape

高度相关（共线）的列

共线的列会减慢训练速度，导致模型难以解释，并降低泛化性能。因此，通常最好删除机器学习中高度相关的每对列中的一个。以下代码识别超过绝对值相关性为0.95的列。

# 设置阈值为0.95
threshold = 0.95# 计算相关性矩阵
corr_matrix = feature_matrix.corr().abs()# 取相关性矩阵的上三角部分
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(np.bool))# 找出相关性大于阈值的列名
to_drop = [column for column in upper.columns if any(upper[column] >= threshold)]

# 打印语句，输出结果为：有{len(to_drop)}个列的相关性大于{threshold}需要删除
print(f'There are {len(to_drop)} columns to drop with correlation > {threshold}')

There are 168 columns to drop with correlation > 0.95

# 删除 feature_matrix 中的指定列
feature_matrix.drop(columns=to_drop, inplace=True)
# inplace=True 表示在原数据上进行修改，不创建新的对象
# 返回修改后的 feature_matrix 的形状
feature_matrix.shape

这些数据清洗操作应该能提高我们模型的泛化性能，并使其更易解释。一些简单的操作可以极大地改善机器学习模型，通常比模型优化更有效。

将数据集分为训练集和测试集

我们将根据日期将数据集分为训练集和测试集。我们将在测试集中使用25%的数据，在训练集中使用75%的数据。根据日期将训练集和测试集分开在时间敏感问题中非常重要，因为它可以防止数据泄漏，并且可以更好地估计模型的泛化性能。在真实数据中，我们的模型将需要对未来进行预测，我们可以通过使用比训练数据更晚的保留集来尝试重新创建这种情况。

# 将feature_matrix中的'time'列转换为日期时间格式
feature_matrix['time'] = pd.to_datetime(feature_matrix['time'])# 输出'time'列的描述统计信息
feature_matrix['time'].describe()

下面的单元格根据时间将数据分割。我们将尝试使用大约30%的数据进行测试，剩下的数据用于训练。

# 定义分割日期
split_date = pd.datetime(2016, 8, 1)# 从特征矩阵中选择小于分割日期的数据作为训练集
train = feature_matrix.loc[feature_matrix['time'] < split_date].copy()# 从特征矩阵中选择大于等于分割日期的数据作为测试集
test = feature_matrix.loc[feature_matrix['time'] >= split_date].copy()# 根据时间对训练集进行排序
train.sort_values(['time'], inplace=True)# 根据时间对测试集进行排序
test.sort_values(['time'], inplace=True)# 打印训练集和测试集的形状
train.shape, test.shape

# 计算训练集的长度除以特征矩阵的长度
result = len(train) / len(feature_matrix)# 返回结果
result

特征准备

下面的代码块将为机器学习准备特征。

对分类特征进行编码

首先，我们需要对特征进行独热编码。在完成这一步之后，我们将对训练数据和测试数据的数据框进行对齐，以确保它们具有相同的列。

# 读取数据并进行one-hot编码
train = pd.get_dummies(train.drop(columns=['time', 'msno'])) # 删除'time'和'msno'列，并对剩余列进行one-hot编码
test = pd.get_dummies(test.drop(columns=['time', 'msno'])) # 删除'time'和'msno'列，并对剩余列进行one-hot编码# 对train和test进行列对齐
train, test = train.align(test, join='inner', axis=1) # 对train和test进行列对齐，只保留两者共有的列
# 输出train和test的形状
print(train.shape, test.shape) # 输出train和test的形状

提取标签

现在我们可以提取标签了。有两个不同的问题：一个是二元分类，即客户在本月是否会流失。另一个是回归问题：下一次流失还有多少天。

# 从train中弹出'label'列，并转换为numpy数组，赋值给y
# 从test中弹出'label'列，并转换为numpy数组，赋值给test_y
y, test_y = np.array(train.pop('label')), np.array(test.pop('label'))# 从train中弹出'days_to_churn'列，并转换为numpy数组，赋值给y_reg
# 从test中弹出'days_to_churn'列，并转换为numpy数组，赋值给test_y_reg
y_reg, test_y_reg = np.array(train.pop('days_to_churn')), np.array(test.pop('days_to_churn'))

# 导入matplotlib.pyplot模块并命名为plt
import matplotlib.pyplot as plt
# 在jupyter notebook中显示图像
%matplotlib inline# 绘制y的直方图
plt.hist(y)
# 设置图像标题为"Label Distribution"
plt.title('Label Distribution')
# 设置y轴标签为"Count"
plt.ylabel('Count')

填充缺失值

我们可以使用列的中位数来填充缺失值。需要注意的是，缺失的测试值将使用相应训练特征的中位数进行填充。

# 将train中的无穷大和负无穷大替换为NaN
train = train.replace([np.inf, -np.inf], np.nan)# 使用train的中位数填充NaN值
train = train.fillna(train.median())

# 检查训练数据是否存在缺失值
np.any(train.isnull())# 检查训练数据是否存在无穷大的值
np.any(np.isinf(train))

# 将test中的无穷大和负无穷大替换为NaN
test = test.replace([np.inf, -np.inf], np.nan)
# 使用train的中位数填充test中的NaN值
test = test.fillna(train.median())

# 检查test中是否存在空值，返回一个布尔值
np.any(test.isnull())# 检查test中是否存在无穷大的值，返回一个布尔值
np.any(np.isinf(test))

现在，由于没有缺失值，并且所有的值都是数值型的，我们的数据已经准备好用于机器学习了。然而，在进行机器学习之前，我们需要弄清楚一个天真的基准会得到什么样的分数。

朴素基准线

对于一个朴素的基准线，我们可以随机猜测一个客户的流失频率与训练数据中的流失频率相同。我们将使用多种不同的指标来评估预测结果。

指标

对于一个不平衡的分类问题，有许多指标需要考虑：

• 接收器操作特性曲线下面积（ROC AUC）：在预测概率在一系列阈值上的表现时，介于0和1之间的度量。
• 精确度得分：真正例数除以预测的总正例数
• 召回率得分：真正例数除以数据中的总实际正例数
• F1得分：精确度和召回率的调和平均值

所使用的确切指标和我们的模型需要达到的阈值取决于业务需求。我们可以在一定程度上调整模型以优化不同的指标。

# 设置随机种子
np.random.seed(50)# 使用二项分布生成随机数，模拟对测试集进行简单猜测
# 参数p为y的平均值，size为测试集的长度
naive_guess = np.random.binomial(1, p=np.mean(y), size=len(test_y))# 输出前10个猜测结果和猜测结果的总和
naive_guess[:10], naive_guess.sum()

from sklearn.metrics import (roc_auc_score, precision_score,recall_score, f1_score)print('Naive Baseline\n')  # 打印Naive Baselineroc = roc_auc_score(test_y, np.repeat(np.mean(y), len(test_y)))  # 计算ROC AUC得分
print(f'ROC AUC: {round(roc, 4)}')  # 打印ROC AUC得分for metric in [precision_score, recall_score, f1_score]:  # 遍历precision_score、recall_score和f1_score函数print(f'{metric.__name__}: {round(metric(test_y, naive_guess), 4)}')  # 打印每个指标的得分

Naive BaselineROC AUC: 0.5
precision_score: 0.0106
recall_score: 0.0354
f1_score: 0.0163

我们可以看到这些指标非常糟糕！一个天真的方法显然并没有提供太多价值。

print(f'The percentage of churns is {100 * round(np.mean(y), 2)}% in the training data.')

The percentage of churns is 4.0% in the training data.

更复杂的模型

为了得到一个可能更好的机器学习模型，我们可以使用随机森林分类器。

我们将使用大部分默认的超参数，但会改变一些以防止过拟合。我们还可以设置class_weight = 'balanced'来尝试抵消这种不平衡的分类问题的影响。

from sklearn.metrics import roc_auc_score, precision_score, recall_score, f1_scoredef evaluate(model, train, y, test, test_y):"""评估机器学习模型的四个指标：ROC AUC、精确率、召回率和F1得分。返回模型和预测结果。"""model.fit(train, y)# 预测概率和标签probs = model.predict_proba(test)[:, 1]preds = model.predict(test)# 计算ROC AUCroc = roc_auc_score(test_y, probs)name = repr(model).split('(')[0]print(f"{name}\n")print(f'ROC AUC: {round(roc, 4)}')# 遍历指标for metric in [precision_score, recall_score, f1_score]:# 使用.__name__属性列出指标名称print(f'{metric.__name__}: {round(metric(test_y, preds), 4)}')return model, preds

# 导入随机森林分类器模型
from sklearn.ensemble import RandomForestClassifier# 创建随机森林分类器模型，并设置参数
model = RandomForestClassifier(n_estimators=100, max_depth=40,min_samples_leaf=50,n_jobs=-1, class_weight='balanced',random_state=50)# 调用evaluate函数对模型进行评估，并返回模型和预测结果
model, preds = evaluate(model, train, y, test, test_y)

RandomForestClassifierROC AUC: 0.9245
precision_score: 0.1246
recall_score: 0.6219
f1_score: 0.2075

模型验证

我们需要检查模型的结果，以确定它是否满足我们的业务需求。这包括查看性能以及特征的重要性。我们希望确保我们的模型表现良好，同时也试图理解它为什么表现良好。

精确率-召回率曲线

调整模型以满足业务需求的最佳方法之一是通过精确率-召回率曲线。这显示了不同阈值下的精确率和召回率的权衡。根据业务要求，我们可以改变分类正例的阈值，以改变真正例、假正例、假负例和真负例之间的平衡。精确率和召回率之间总会存在权衡，但我们可以通过视觉和定量评估模型来寻找合适的平衡点。

from sklearn.metrics import precision_recall_curve, confusion_matriximport matplotlib.pyplot as plt
%matplotlib inlineplt.style.use('seaborn')def plot_precision_recall(test_y, probs, title='Precision Recall Curve', threshold_selected=None):"""Plot a precision recall curve for predictions. Source: http://scikit-learn.org/stable/auto_examples/model_selection/plot_precision_recall.html#sphx-glr-auto-examples-model-selection-plot-precision-recall-py"""precision, recall, threshold = precision_recall_curve(test_y, probs)plt.figure(figsize=(10, 8))# In matplotlib < 1.5, plt.fill_between does not have a 'step' argumentstep_kwargs = ({'step': 'post'})plt.step(recall, precision, color='b', alpha=0.2,where='post')plt.fill_between(recall, precision, alpha=0.2, color='b', **step_kwargs)plt.xlabel('Recall', size=18)plt.ylabel('Precision', size=18)plt.ylim([0.0, 1.05])plt.xlim([0.0, 1.0])plt.title(title, size=20)plt.xticks(size=14)plt.yticks(size=14)if threshold_selected:p = precision(np.where(threshold == threshold_selected)[0])r = recall(np.where(threshold == threshold_selected)[0])plt.scatter(r, p, marker='*', size=200)plt.vlines(r, ymin=0, ymax=p, linestyles='--')plt.hlines(p, xmin=0, xmax=r, linestyles='--')pr = pd.DataFrame({'precision': precision[:-1], 'recall': recall[:-1],'threshold': threshold})return prprobs = model.predict_proba(test)[:, 1]
pr_data = plot_precision_recall(test_y, probs, title='Precision-Recall Curve for Random Forest')

我们可以查询数据框以找到给定精确度或召回率所需的阈值。例如，要找到精确度为25%的阈值，我们使用以下代码：

# 筛选出精度大于等于0.25的数据
precision_above = pr_data.loc[pr_data['precision'] >= 0.25].copy()# 按照召回率从大到小排序
precision_above.sort_values('recall', ascending=False, inplace=True)# 返回前5行数据
precision_above.head()

调整业务需求

假设我们的模型要求有75%的召回率。这意味着我们的模型能够找到数据中75%的真实流失情况。在这个假设下，我们将继续完成本笔记的其余部分。为了找到阈值，我们使用以下公式：

# 设置召回率阈值为0.75
recall_attained = 0.75# 从pr_data中筛选出召回率大于等于阈值的数据，并进行拷贝
recall_above = pr_data.loc[pr_data['recall'] >= recall_attained].copy()# 按照精确率降序排序
recall_above.sort_values('precision', ascending=False, inplace=True)# 返回排序后的前几行数据
recall_above.head()

# 获取recall_above中第一行第一列的值，即达到的精确度
precision_attained = recall_above.iloc[0, 0]
# 获取recall_above中第一行最后一列的值，即所需的阈值
threshold_required = recall_above.iloc[0, -1]# 打印结果，包括阈值、召回率和精确度
print(f'At a threshold of {round(threshold_required, 4)} the recall is {100 * recall_attained:.2f}% and the precision is {round(100 * precision_attained, 4)}%')

At a threshold of 0.4072 the recall is 75.00% and the precision is 9.4712%

这意味着为了识别出75%的实际流失客户，我们必须接受只有9.5%的预测阳性结果实际上是流失客户。

# 定义一个函数，用于绘制Precision-Recall曲线
# 参数：
#   test_y: 测试集的真实标签
#   probs: 预测的概率值
#   title: 图表的标题，默认为'Precision Recall Curve'
#   threshold_selected: 选定的阈值，默认为None
def plot_precision_recall(test_y, probs, title='Precision Recall Curve', threshold_selected=None):"""Plot a precision recall curve for predictions. Source: http://scikit-learn.org/stable/auto_examples/model_selection/plot_precision_recall.html#sphx-glr-auto-examples-model-selection-plot-precision-recall-py"""# 计算Precision-Recall曲线的precision、recall和thresholdprecision, recall, threshold = precision_recall_curve(test_y, probs)# 创建一个10x10的图表plt.figure(figsize=(10, 10))# 在matplotlib < 1.5中，plt.fill_between函数没有'step'参数step_kwargs = ({'step': 'post'})# 绘制Precision-Recall曲线的步进图plt.step(recall, precision, color='b', alpha=0.2,where='post')# 填充Precision-Recall曲线的区域plt.fill_between(recall, precision, alpha=0.2, color='b', **step_kwargs)# 设置x轴和y轴的标签plt.xlabel('Recall', size=24)plt.ylabel('Precision', size=24)# 设置y轴的范围为[0.0, 1.05]plt.ylim([0.0, 1.05])# 设置x轴的范围为[0.0, 1.0]plt.xlim([0.0, 1.0])# 设置图表的标题plt.title(title, size=24)# 设置x轴和y轴的刻度大小plt.xticks(size=18)plt.yticks(size=18)# 如果指定了选定的阈值if threshold_selected:# 根据阈值找到对应的precision和recallp = precision[np.where(threshold == threshold_selected)[0]]r = recall[np.where(threshold == threshold_selected)[0]]# 在图表上绘制选定阈值的点plt.scatter(r, p, marker='*', s=600, c='r')# 绘制垂直线和水平线plt.vlines(r, ymin=0, ymax=p, linestyles='--')plt.hlines(p, xmin=0, xmax=r, linestyles='--')# 在图表上添加阈值的文本plt.text(r - 0.1, p + 0.15,s=f'Threshold: {round(threshold_selected, 2)}', size=20, fontdict={'weight': 1000})# 在图表上添加precision和recall的文本plt.text(r - 0.2, p + 0.075,s=f'Precision: {round(100 * p[0], 2)}% Recall: {round(100 * r[0], 2)}%', size=20,fontdict={'weight': 1000})# 创建一个包含precision、recall和threshold的DataFrame，并返回pr = pd.DataFrame({'precision': precision[:-1], 'recall': recall[:-1],'threshold': threshold})return pr

pr_data = plot_precision_recall(test_y, probs, title='Precision-Recall Curve for Tuned Random Forest',threshold_selected=threshold_required)

混淆矩阵

混淆矩阵通常是一种可视化预测结果的有用方式。它将真实值显示在顶部行，将预测值显示在底部行。通过查看不同的单元格，我们可以看到模型表现良好和不良的地方。

我们将使用上面确定的阈值来构建混淆矩阵。

from sklearn.metrics import confusion_matrix
import itertoolsdef plot_confusion_matrix(cm, classes,normalize=False,title='Confusion matrix',cmap=plt.cm.YlOrRd):"""这个函数打印并绘制混淆矩阵。可以通过设置`normalize=True`来进行归一化。来源：http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html"""if normalize:cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]print("Normalized confusion matrix")else:print('Confusion matrix, without normalization')print(cm)plt.style.use('bmh')plt.figure(figsize=(9, 9))plt.imshow(cm, interpolation='nearest', cmap=cmap)plt.title(title, size=22)plt.colorbar()tick_marks = np.arange(len(classes))plt.xticks(tick_marks, classes, rotation=45, size=20)plt.yticks(tick_marks, classes, size=20)fmt = '.2f' if normalize else 'd'thresh = cm.max() / 2.for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):plt.text(j, i, format(cm[i, j], fmt),horizontalalignment="center",color="white" if cm[i, j] > thresh else "black",size=20)plt.grid(None)plt.ylabel('True label', size=22)plt.xlabel('Predicted label', size=22)plt.tight_layout()

# 设定阈值，将概率大于等于该阈值的预测结果设为1，否则为0
threshold_required = 0.5
preds = np.zeros(len(test_y))
preds[probs >= threshold_required] = 1# 生成混淆矩阵并绘制
cm = confusion_matrix(test_y, preds)
plot_confusion_matrix(cm, classes=['No Churn', 'Churn'],title='Churn Confusion Matrix')

Confusion matrix, without normalization
[[84975  6882][  240   720]]

如果我们满足我们的业务需求，这将是我们在新数据上表现的最佳预测。该模型能够识别出75%的流失客户，而基线只有约3%。精确度从基线的1%增加到9%，相对增长超过900%。

特征重要性

作为一种尝试理解模型决策方式的方法之一，我们可以查看最重要的特征。重要性的绝对值并不像特征在随机森林中构建决策树时如何有效地分离类别那样有用，相对排名的重要性更有意义。

# 创建一个DataFrame对象fi，包含一个名为'importance'的列，列的值为model.feature_importances_，索引为train.columns
fi = pd.DataFrame({'importance': model.feature_importances_}, index=train.columns)# 对fi按照'importance'列的值进行降序排序
fi = fi.sort_values('importance', ascending=False)# 返回排序后的前10行数据
fi.head(10)

# 从数据集中选择前10行的'importance'列，并绘制水平条形图
fi.iloc[:10]['importance'].plot.barh(color='r', edgecolor='k', figsize=(14, 10), linewidth=2)# 获取当前的坐标轴对象
ax = plt.gca()# 反转y轴的方向，使得重要性从上到下递减
ax.invert_yaxis()# 设置x轴刻度标签的大小为20
plt.xticks(size=20)# 设置y轴刻度标签的大小为18
plt.yticks(size=18)# 设置图表标题为'Most Important Features'，字体大小为28
plt.title('Most Important Features', size=28)# 返回结果，包含代码和注释

进行预测

现在我们将使用训练好的模型对保留的测试集进行预测。我们可以根据概率进行预测，然后使用我们选择的阈值将其转化为标签。

# 使用模型对测试数据进行预测，并获取预测结果的概率值
new_probs = model.predict_proba(test)[:, 1]# 获取时间大于等于分割日期的样本的用户ID和时间
oos_ids = list(feature_matrix.loc[feature_matrix['time'] >= split_date, 'msno'])
oos_cutoff_time = list(feature_matrix.loc[feature_matrix['time'] >= split_date, 'time'])# 创建一个DataFrame来存储预测结果
prediction_df = pd.DataFrame({'msno': oos_ids, 'time': oos_cutoff_time,'probability': new_probs})# 根据设定的阈值，将概率值转换为二分类的预测结果
prediction_df['prediction'] = prediction_df['probability'] > threshold_required# 随机抽样10个样本进行查看
prediction_df.sample(10)

# 绘制概率分布直方图，分成20个区间，边缘颜色为黑色
prediction_df['probability'].plot.hist(bins=20, edgecolor='k')# 在图中添加红色竖线，表示阈值
threshold_required = 0.5
plt.axvline(x=threshold_required, color='r', linewidth=2)# 设置图的标题
plt.title('Distribution of Predicted Probabilities')# 显示图像
plt.show()

模型相当有信心，大多数预测结果不是流失。此外，有一些概率值与经验累积分布函数中的数值完全相同。

# 定义一个函数ecdf，用于计算经验累积分布函数（ECDF）
def ecdf(x):n = len(x)  # 获取输入数据x的长度x = np.sort(x)  # 对输入数据x进行排序y = np.arange(1, n + 1) / n  # 计算y值，即每个数据点的累积概率return x, y  # 返回排序后的x和对应的累积概率y

# 计算经验累积分布函数
xs, ys = ecdf(prediction_df['probability'])# 绘制经验累积分布函数曲线
plt.plot(xs, ys, marker='.')# 设置图表标题
plt.title('ECDF of Predicted Probobabilities')# 在图表上添加红色垂直线，表示阈值
plt.axvline(x=threshold_required, color='r', linewidth=2)# 设置x轴标签
plt.xlabel('Probability')# 设置y轴标签
plt.ylabel('Percentile')# 返回结果
plt.show()

业务价值分析

使用模型的指标，我们可以对我们的解决方案的业务价值进行分析。我们将使用精确度和召回率以及一些假设。

• 典型计划价格 = 150（新台币）
• 降价计划价格 = 130（新台币）
• 召回率 = 75%
• 精确度 = 9.5%
• 转化率 = 75%

$$\text{召回率}=\frac{TP}{TP+FN}$$

$$\text{精确度}=\frac{TP}{TP+FP}$$

我们可以将我们的分析扩展到整个数据集，因为我们只使用了其中的一个子集进行建模。我们假设我们能够在整个数据集上实现相同的性能，这是合理的，因为模型的准确性通常随着使用的数据量增加而提高。

plan_price = 150
r_plan_price = 130
recall = recall_attained
precision = precision_attained
conversion_rate = 0.75# Find total number of members
n_members = pd.read_csv(f'{CWD}/data/members_v3.csv', usecols = ['msno']).shape[0]
monthly_revenue = n_members * plan_price
churn_rate = np.mean(feature_matrix['label'])churns = int(churn_rate * n_members)
# Find the typical monthly revenue lost to churned customers
revenue_lost_churns = n_members * churn_rate * plan_price
print(f'Typical monthly revenue lost to {churns} churned customers = ${revenue_lost_churns:,.2f} (NTD).')
print(f'Typical total monthly revenue = ${monthly_revenue:,.2f}.')
print(f'Churns losses represent {100 * (revenue_lost_churns / monthly_revenue):.2f}% of monthly revenue.')

Typical monthly revenue lost to 191597 churned customers = $28,739,586.27 (NTD).
Typical total monthly revenue = $1,015,420,950.00.
Churns losses represent 2.83% of monthly revenue.

# 计算整个数据集的统计信息# 计算真正例数
true_positives = int(churns * recall)# 计算假负例数
false_negatives = int(churns - true_positives)# 计算假正例数
false_positives = int((true_positives * (1 - precision)) / precision)# 打印结果
print(f'True positives: {true_positives}; False negatives: {false_negatives}; False positives: {false_positives}.')

True positives: 143697; False negatives: 47900; False positives: 1373503.

作为一个合理性检查，我们将确保精确度和召回率指标正确。

# 计算精确率的公式是：真阳性 / (真阳性 + 假阳性)
(true_positives) / (true_positives + false_positives)

# 计算精确率的公式是：真阳性 / (真阳性 + 假阴性)
(true_positives) / (true_positives + false_negatives)

事情看起来很顺利。

# 计算误报造成的损失
revenue_lost_false_positives = false_positives * (plan_price - r_plan_price)# 计算漏报造成的损失
revenue_lost_false_negatives = false_negatives * plan_price# 计算真正报告带来的收入
revenue_recouped_true_positives = conversion_rate * (true_positives * r_plan_price)# 打印误报造成的成本和漏报造成的成本
print(f'Cost from false positives = ${revenue_lost_false_positives:,.2f} (NTD); Cost from false negatives = ${revenue_lost_false_negatives:,.2f} (NTD)')# 打印真正报告带来的收入
print(f'Revenue recouped from true positives = ${revenue_recouped_true_positives:,.2f} (NTD).')

Cost from false positives = $27,470,060.00 (NTD); Cost from false negatives = $7,185,000.00 (NTD)
Revenue recouped from true positives = $14,010,457.50 (NTD).

# 计算总效益，公式为：总效益 = 流失收入 - （-回收的收入 + 错失的收入 + 错失的流失）
total_effect = revenue_lost_churns - (-revenue_recouped_true_positives + revenue_lost_false_positives + revenue_lost_false_negatives)# 将总效益转换为美元，汇率为0.033
us_dollars = total_effect * 0.033# 打印总效益和转换后的美元金额
print(f'Total Effect of identifying churns ${total_effect:,.2f} (NTD) = ${us_dollars:,.2f} (USD).')# 计算总效益占流失收入的百分比
percentage = 100 * (total_effect / revenue_lost_churns)# 打印总效益占流失收入的百分比
print(f'This represents {percentage:.2f}% of the losses due to churns.')

Total Effect of identifying churns $8,094,983.77 (NTD) = $267,134.46 (USD).
This represents 28.17% of the losses due to churns.

我们的模型已成功解决了业务问题。这确实需要一些假设，但通过进一步的改进，我们的模型可能能够提供更大的价值。

结论

我们最终调整的模型能够显著提高比朴素基准模型的性能。我们现在可以使用这个模型来预测未来可能流失的客户。对业务回报的分析也显示出最终模型带来了显著的价值。然后，预测结果将交给客户参与团队，希望能减少流失的客户数量。

解决这个问题的框架 - 以及解决任何机器学习问题的框架 - 是：

1. 预测工程：定义业务目标，将其转化为机器学习任务，并从数据中创建一组带有截止时间的标记历史示例。
2. 特征工程：使用标记时间自动构建每个标记的数百个相关和有效的特征。
3. 建模：使用在常见的Python库中实现的机器学习算法，训练模型以从特征中预测标签。根据业务需求验证和调整模型，然后对新数据进行预测。

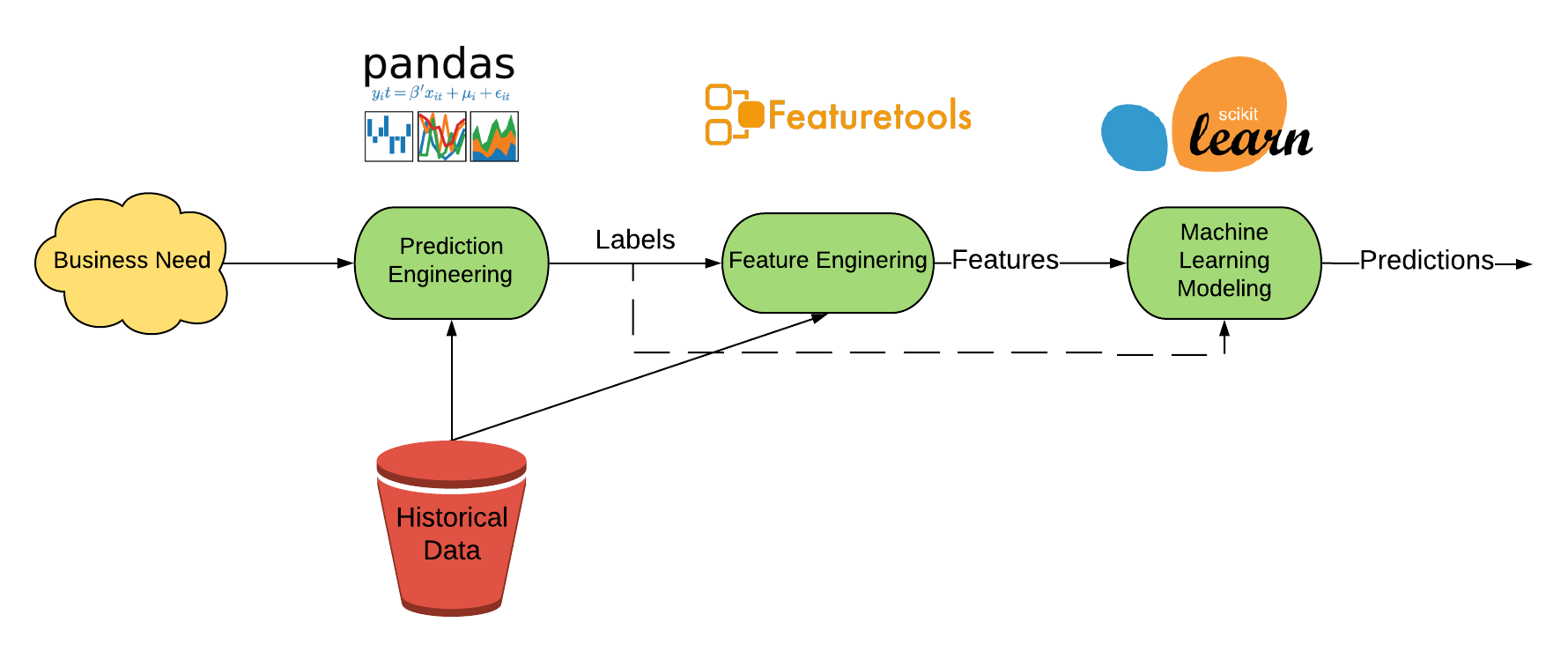
这种方法解决了许多问题：它标准化了传统上凭经验解决机器学习问题的过程，并且它是通用的，几乎可以在相同数据集上用相同的代码解决多个预测问题。机器学习的好处一直局限于少数几家公司，这既是因为缺乏共享语言来表达和解决问题，也是因为每个解决方案都需要定制代码，并且必须完全重新构建以解决不同的预测问题。通过将解决机器学习问题所需的过程编码化，我们旨在使公司更容易使用这种变革性技术。

此外，该框架允许数据科学家使用现有工具填充细节，从而实现模型管道的快速开发和部署。机器学习的成就已经令人印象深刻，但是有了这样的支架，其好处可以扩展到更广泛的人群。