AtCoder Beginner Contest 206（Sponsored by Panasonic）（补题）

本文主要是介绍AtCoder Beginner Contest 206（Sponsored by Panasonic）（补题），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

C - Swappable

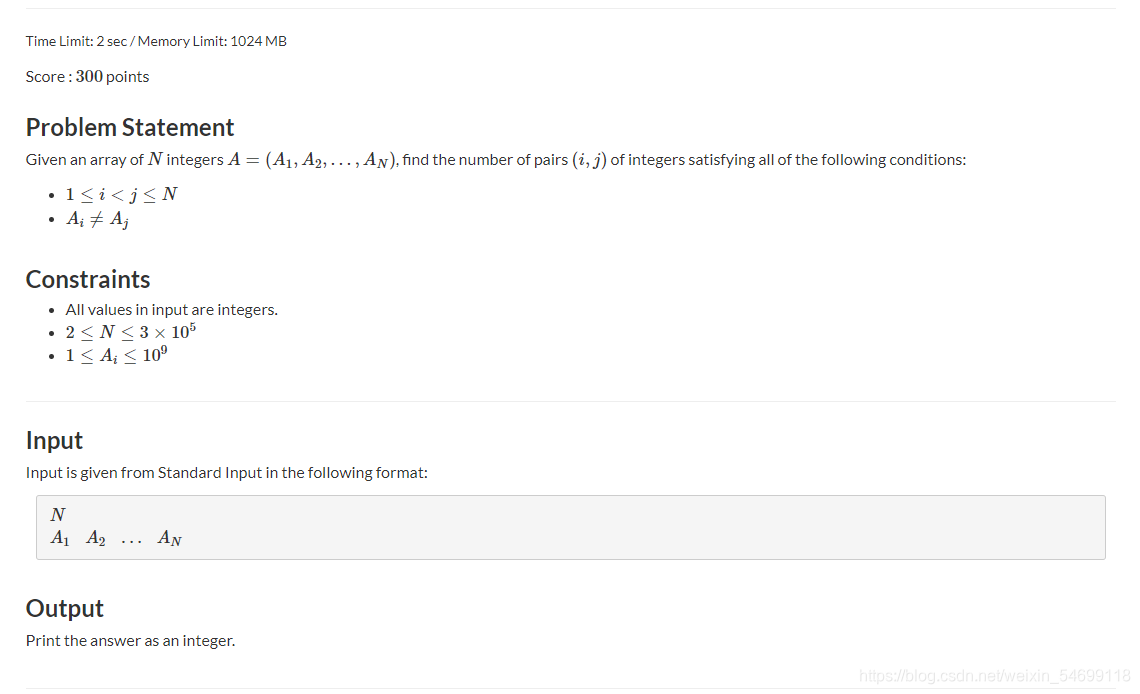
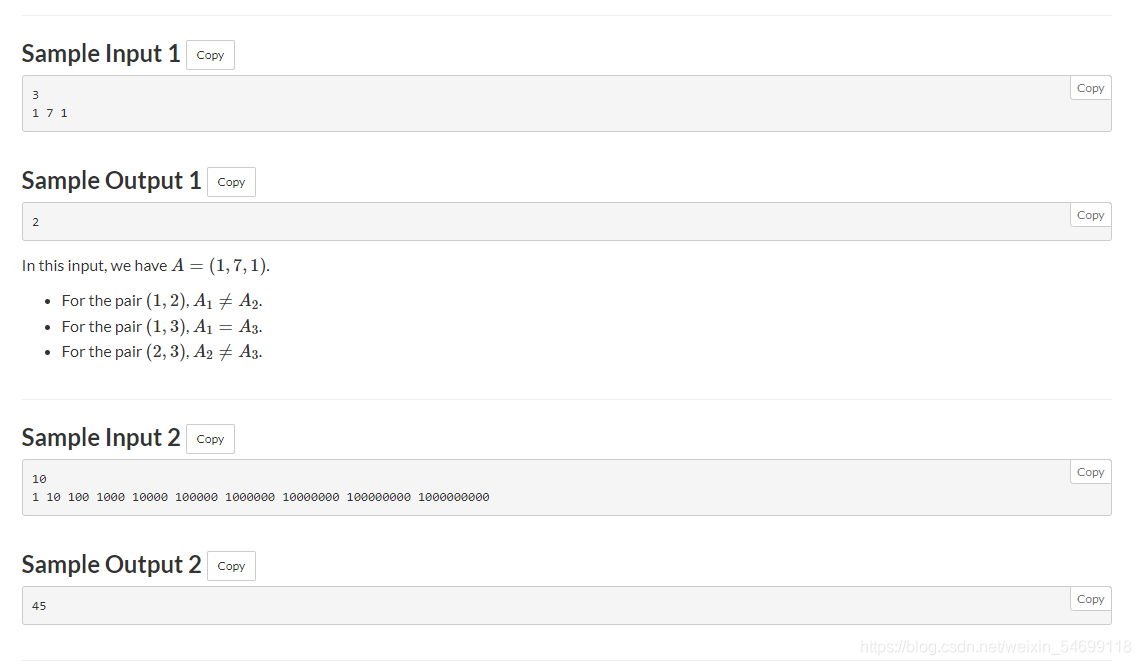
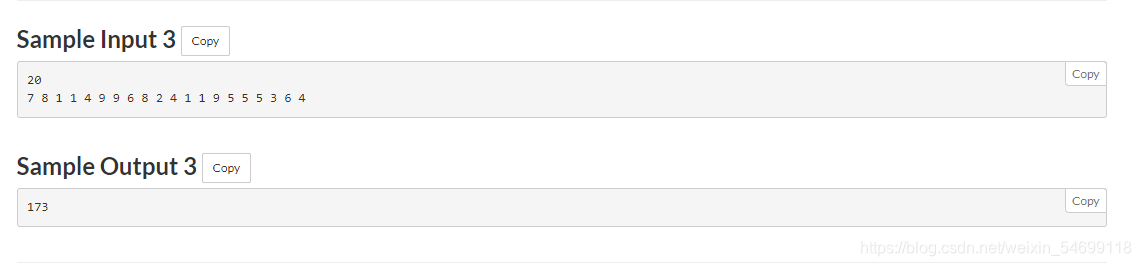
在这里插入图片描述

题意： 给n个数，问有多少对数,1<=i<j<=N, $A_i$ != $A_j$ ，问有多少对数吗？
思路：
思路1： 先排序，枚举每个 $a_i$ ，然后看有多少个大于 $a_i$ ,大于 $a_i$ 的就是 $a_j$ ，不用找小于 $a_i$ 的，因为小于 $a_i$ 枚举的时候，匹配过 $a_i$ 了，不用重复寻找。
思路2： 可以用所有的数对，减去满足 $A_i==A_j$ 的数量，就是满足的数量。总数就是n*(n-1)/2,再用桶记录其中的数量就行。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 3e5 + 10;
ll a[N];
int main() {ll n;cin >> n;for (int i = 0; i < n; i++) {scanf("%lld", &a[i]);}sort(a, a + n);ll res = 0;for (int i = 0; i < n; i++) {res += (n - (upper_bound(a + i + 1, a + n, a[i]) - a));}cout << res << endl;return 0;
}

#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10;
#define ll long long
map<int, int> m;int n;int main() {scanf("%d", &n);ll ans = (ll)(n - 1) * n / 2;for (int i = 1; i <= n; i++) {int a;scanf("%d", &a);ans -= (ll)m[a];++m[a];}printf("%lld\n", ans);return 0;
}

D - KAIBUNsyo

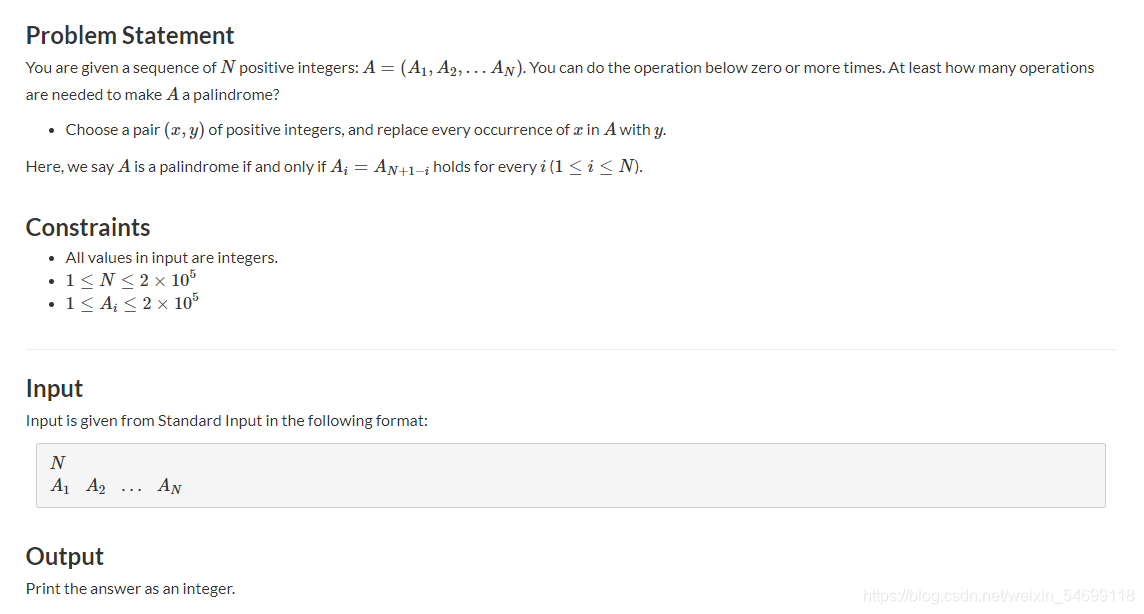
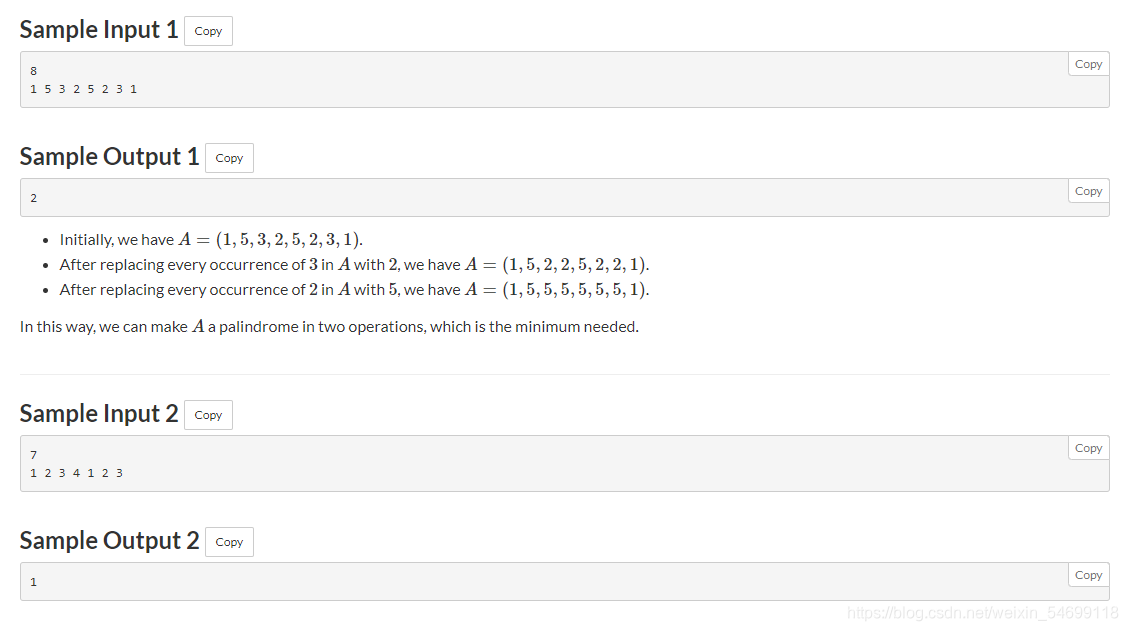
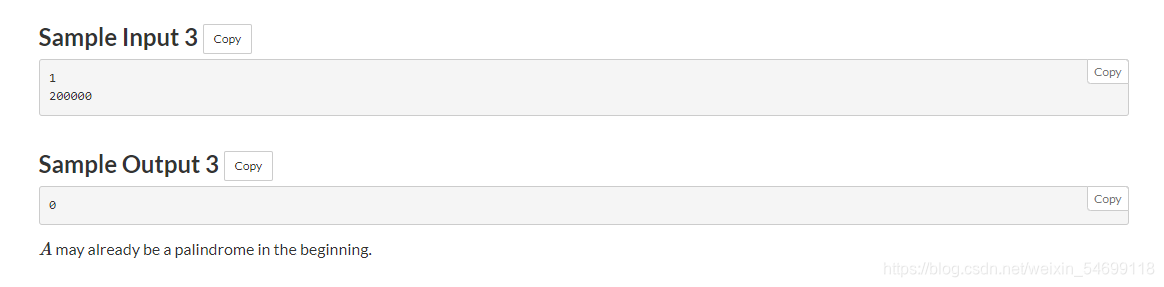
在这里插入图片描述

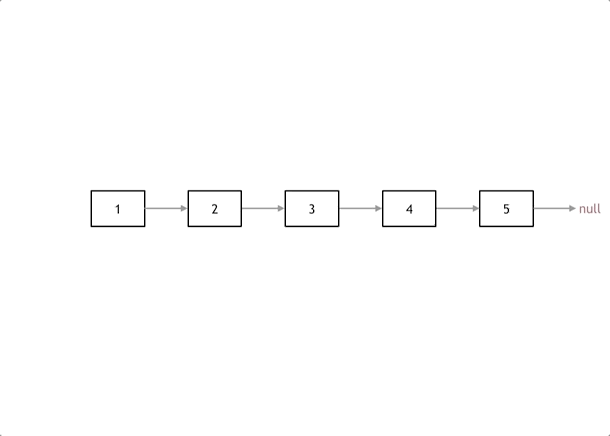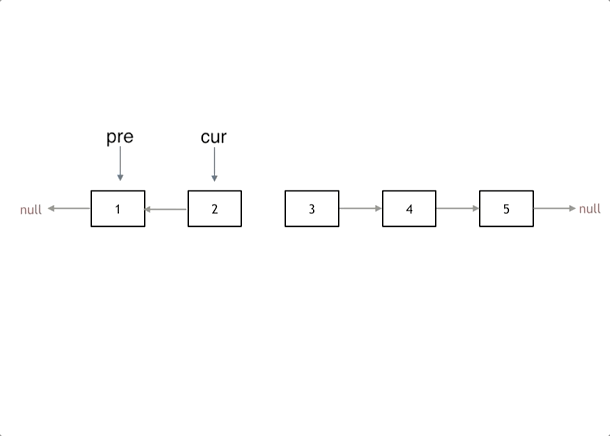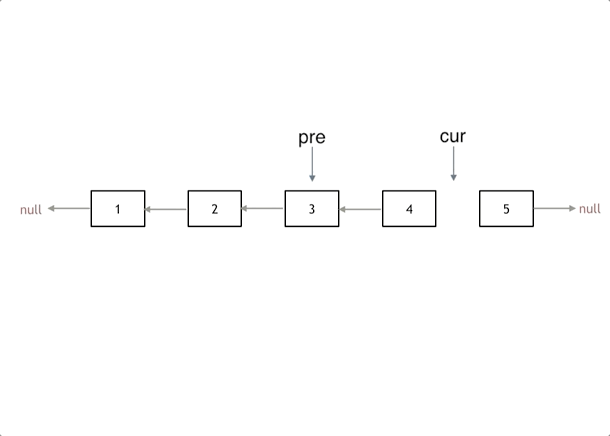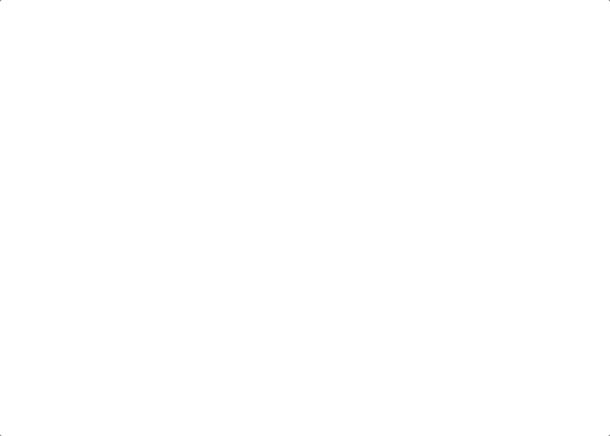
题意： 给n个数，有一种操作，就是令数组中所有等于 $x$ 的数全部转变为 $y$ ,问最少操作几次，才能形成回文数组。
思路： 把 $x$ 变成 $y$ ，可以想成在 $x$ 和 $y$ 之间连一条边，代表在一个连通块中，在一个连通块中，代表连通块的数最后都要变成其中一个数（可以直接都变成祖先节点），而要将一个连通块中的数都变成一个数，那就要看连通块中有几个结点，转变次数就是除了祖先节点以为点的数量，也就是看有几个 $f a [i]! = i$ , $f a [i] = = i$ 都是祖先节点，这样就
每次就是对称的两个点，是不是同一个数字，是否对称，不对称的话，就要放一个连通块中，表示要操作。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int fa[N];
int a[N];int find(int x) {if (x != fa[x]) fa[x] = find(fa[x]);return fa[x];
}
void Union(int a, int b) {if (find(a) != find(b)) {fa[find(a)] = find(b);}
}int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; i++) {scanf("%d", &a[i]);}for (int i = 1; i <= N; i++) {fa[i] = i;}for (int l = 1, r = n; l < r; l++, r--) {Union(a[l], a[r]);}int ans = 0;for (int i = 1; i <= N; i++) {ans += (fa[i] != i);}printf("%d\n", ans);return 0;
}