水壶问题与裴蜀定理

水壶问题

题目有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶，从而可以得到恰好 z升 的水？
如果可以，最后请用以上水壶中的一或两个来盛放取得的 z升 水。
你允许：
1-装满任意一个水壶
2-清空任意一个水壶
3-从一个水壶向另外一个水壶倒水，直到装满或者倒空
因此可以说明，每次操作会使得最终的结果变化**（±）x或者（±）y**，都是整数，变化（x-y）类型其实也是一个x,以及一个-y。

比如a=3, b = 5,目标值是4，应该怎么组装呢？

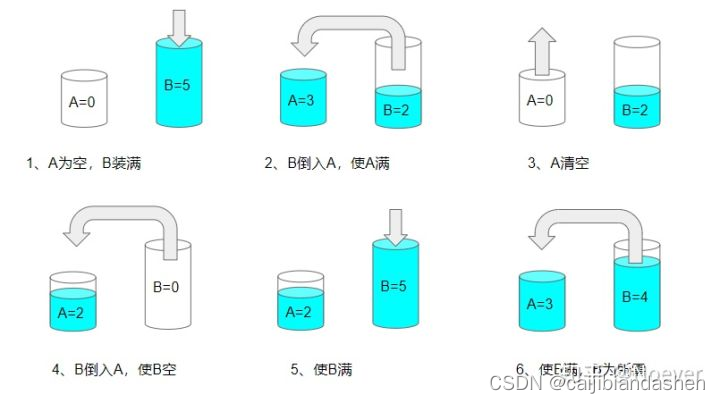
得到 2b - 2a = 目标值
假设xa+yb= c,如果有解，根据裴蜀定理，则c应该是x和y的最大公约数的整数倍

裴蜀定理（或贝祖定理）得名于法国数学家艾蒂安·裴蜀，说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性不定方程（称为裴蜀等式）：若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。百度百科
解法
回到本题，则只需要求是否有解就可以了，因为瓶子只有两个，因此，
如果目标和大于二者之和就无解。
如果是0，有解
如果一个为0，则目标值必须等于另一个，否则无解
代码

public boolean canMeasureWater(int jug1Capacity, int jug2Capacity, int targetCapacity) {//根据裴蜀定理：对于ax+by=z, 当且仅当，z是a和b的最大公约数的倍数时，方程有解。if (targetCapacity > jug1Capacity + jug2Capacity) return false;if (jug1Capacity == 0) return targetCapacity ==jug2Capacity;if (jug2Capacity == 0) return targetCapacity == jug1Capacity;if (targetCapacity == 0 || targetCapacity == jug1Capacity || targetCapacity == jug2Capacity || targetCapacity == jug1Capacity + jug2Capacity) return true;//因为x、y、z已经知道了,就只要z是x+y的最大公约数的整数倍就可以有答案int answer = 1;int min = Math.min(jug1Capacity, jug2Capacity);for (int i = 1; i <= min; i++) { if (jug1Capacity % i == 0 && jug2Capacity % i == 0) answer = i; }return targetCapacity % answer == 0;}

参考：

1. Die Hard Problem（水壶问题）–算法中的数学思想
2. 裴蜀定理

还可以使用递归解决
代码

/***每次操作一共有以下几种情况：* 1.把 X 壶的水灌进 Y 壶，直至灌满或倒空；* 2.把 Y 壶的水灌进 X 壶，直至灌满或倒空；* 3.把 X 壶灌满；* 4.把 Y 壶灌满；* 5.把 X 壶倒空；* 6.把 Y 壶倒空。*/public boolean canMeasureWater(int x, int y, int z) {//使用栈来模拟递归过程Deque<int[]> stack = new LinkedList<int[]>();stack.push(new int[]{0, 0});//每次进行剪枝操作防止无限递归Set<Long> seen = new HashSet<Long>();while (!stack.isEmpty()) {if (seen.contains(hash(stack.peek()))) {stack.pop();continue;}seen.add(hash(stack.peek()));int[] state = stack.pop();//如果有一个满足条件，就返回int remain_x = state[0], remain_y = state[1];if (remain_x == z || remain_y == z || remain_x + remain_y == z) {return true;}// 把 X 壶灌满。stack.push(new int[]{x, remain_y});// 把 Y 壶灌满。stack.push(new int[]{remain_x, y});// 把 X 壶倒空。stack.push(new int[]{0, remain_y});// 把 Y 壶倒空。stack.push(new int[]{remain_x, 0});// 把 X 壶的水灌进 Y 壶，直至灌满或倒空。stack.push(new int[]{remain_x - Math.min(remain_x, y - remain_y), remain_y + Math.min(remain_x, y - remain_y)});// 把 Y 壶的水灌进 X 壶，直至灌满或倒空。stack.push(new int[]{remain_x + Math.min(remain_y, x - remain_x), remain_y - Math.min(remain_y, x - remain_x)});}return false;}public long hash(int[] state) {return (long) state[0] * 1000001 + state[1];}