水壶专题
字节跳动面试题 —— 水壶问题
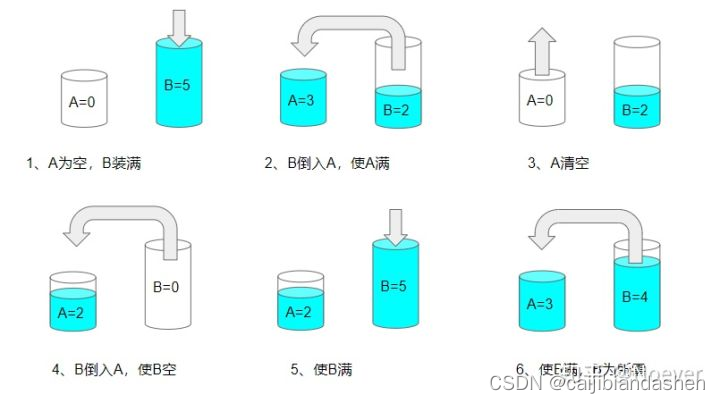
点击上方“朱小厮的博客”,选择“设为星标” 回复”1024“获取独家整理的学习资料 原题:给你一个装满水的 8 升满壶和两个分别是 5 升、3 升的空壶,请想个优雅的办法,使得其中一个水壶恰好装 4 升水,每一步的操作只能是倒空或倒满。 理解了这个题目的意思之后,我们的第一个方法肯定就是使用强大的脑力来进行暴力破解法,瓶子里的水在我们的脑子里颠三倒四,但是脑子有可能没那么清晰,想了几步之
C++ | Leetcode C++题解之第365题水壶问题
题目: 题解: class Solution {public:bool canMeasureWater(int x, int y, int z) {if (x + y < z) {return false;}if (x == 0 || y == 0) {return z == 0 || x + y == z;}return z % gcd(x, y) == 0;}};
Java | Leetcode Java题解之第365题水壶问题
题目: 题解: class Solution {public boolean canMeasureWater(int x, int y, int z) {if (x + y < z) {return false;}if (x == 0 || y == 0) {return z == 0 || x + y == z;}return z % gcd(x, y) == 0;}public int
请马上停用这种水壶,长期喝它烧的水,后果很严重!很多人家里几乎都用!
如果你家里用这种不锈钢水壶烧水,请马上停止使用!因为你的水壶可能正在释出重金属! class="video_iframe" src="http://v.qq.com/iframe/player.html?vid=c0189yux4yw&auto=0" width="300" height="150" frameborder="0" scrolling="no" allowfull
LeetCode 365. 水壶问题(数论)
Description 有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶,从而可以得到恰好 z升 的水? 如果可以,最后请用以上水壶中的一或两个来盛放取得的 z升 水。 你允许: 装满任意一个水壶 清空任意一个水壶 从一个水壶向另外一个水壶倒水,直到装满或者倒空 示例 1: (From the famous "Die Hard" example)输入:
智能烧水壶(WIFI版)03——温度采集和过温报警功能实现篇
前言 前面我们已经创建好产品并建立起app端和设备端的连接,接下来我们将实现智能烧水壶的温度采集和过温报警功能。 一、智能烧水壶的功能设定 智能烧水壶的功能设定如下表,我们将整个智能烧水壶拆分成几个模块,逐个实现功能;本文实现烧水壶的温度采集和声音报警功能,温度采集主要用于水温的温控调节,当温度高于105摄氏度时说明水壶已经处于干烧状态,此时蜂鸣器进行声音报警。 功能说明煮沸触摸按键1,
LeetCode解法汇总365. 水壶问题
目录链接: 力扣编程题-解法汇总_分享+记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 描述: 有两个水壶,容量分别为 jug1Capacity 和 jug2Capacity 升。水的供应是无限的。确定是否有可
力扣365-水壶问题
水壶问题 题目链接 解题思路 假设两个水壶分别为A,B,容量为a,b;想要凑出C升的水将A,B两壶看作一个整体那么,这个整体只存在四种操作+a,-a,+b,-b;+a:就是将A壶装满-a:就是将A壶清空+b:就是将B壶装满-b:就是将B壶清空想要凑出C升的水壶,需要满足xa+yb=c即我们需要对A壶进行x次操作,对B壶进行y次操作,使得可以凑出C升的水要想使得xa+yb=c成立,由裴蜀定理知
初等数论,LeetCode 365. 水壶问题
一、题目 1、题目描述 有两个水壶,容量分别为 jug1Capacity 和 jug2Capacity 升。水的供应是无限的。确定是否有可能使用这两个壶准确得到 targetCapacity 升。 如果可以得到 targetCapacity 升水,最后请用以上水壶中的一或两个来盛放取得的 targetCapacity 升水。 你可以: 装满任意一个水壶清空任意一个水壶从一个水壶向另外一个水壶
leetcode第365题:水壶问题
有两个水壶,容量分别为 jug1Capacity 和 jug2Capacity 升。水的供应是无限的。确定是否有可能使用这两个壶准确得到 targetCapacity 升。 如果可以得到 targetCapacity 升水,最后请用以上水壶中的一或两个来盛放取得的 targetCapacity 升水。 你可以: 装满任意一个水壶清空任意一个水壶从一个水壶向另外一个水壶倒水,直到装满或者倒空
uva571 - Jugs(水壶)
贴出以为大神的分析。。。。简明易懂 本题只要求给出一个解,不要求最优。所给的两个罐子容量一定互质,因此必然可以倒出从0到大罐容量间的任何整数值。原理是若A,B互质,则最小公倍数为A×B,即不存在一个1 < n < B,使得nA能被B整除。令r = nA mod B(mod为取模操作),那么当n从0到B-1变化时,r可以取到0到B-1之间的任何值。这个是很容易证明的,但我的证明过程非常不专业,