本文主要是介绍低秩恢复算法(图像去噪)_米米米米粒口红_新浪博客,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
声明:本博客为整料整理,引用的地方均有注明。如需转载,请注明出处!
低秩矩阵恢复算法
概述
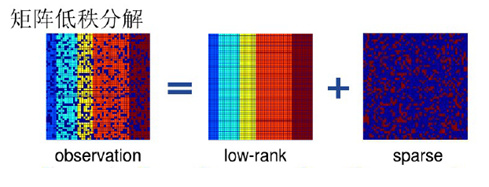
近几年,低秩矩阵恢复(LRMR)广泛用于图像处理用途图像恢复,比如去噪、去模糊等。一幅清晰的自然图像其数据矩阵往往是低秩或者近似低秩的,但存在随机幅值任意大但是分布稀疏的误差破坏了原有数据的低秩性。低秩矩阵恢复是将退化图像看做一组低维数据加上噪声形成的,因此退化前的数据就可以通过低秩矩阵来逼近。
设B为模糊图像,根据低秩分解有B=I+N,其中I为清晰图像,是低秩的。N为噪声具有稀疏性。

秩[1]
设在矩阵A中有一个不等于0的r阶子式D,且所有r+1阶子式(如果存在的话)全等于0,那么D称为矩阵A的最高阶非零子式,数r称为矩阵A的秩,记作R(A)。并规定零矩阵的秩等于0.
求解方法:对矩阵作初等行变换为行阶梯矩阵,其中非零行的个数为矩阵的秩。其物理意义矩阵中的最大不相关的向量的个数。
低秩矩阵(低秩)
低秩是指矩阵的秩比较小,而矩阵的低秩性是指矩阵的秩相对矩阵的行数或列数而言很小[2]。
由矩阵秩的定义知道,若将图像看成一个矩阵,那么它的基的数量越少,基对应的线性无关向量数量就越少,矩阵的秩就越小。当它远远小于矩阵的大小的时候,图像就是低秩的。低秩矩阵的每行或者每列都可以用其他的行或者列线性表示,这说明这个矩阵包含了大量的冗余信息。利用这种冗余信息可以对确实图像信息进行恢复,可以将多出来的噪声信息进行去除,还可以对错误的图像信息进行恢复[3]。
图像处理中,rank可以理解为图像所包含的信息的丰富程度,在现实生活中,一张图片大部分是相似的。比如一张大草原的图片

可以理解为,草原是由很多草组成的,而草是相似的,所以如果全是草,那么这张图所包含的信息量是很少的的,因为可以理解为草是草的复制品。而上图的蒙古包,人,马之类的则可以理解为图片所包含的信息,实际上,相对于只有草的草原图片和有草和蒙古包的草原图片,后者的秩是较高的。也就是说,图片中比较突兀的成分,比如蒙古包,比如人像照片中的红眼亮点,会增加图像矩阵的秩。而现实生活中一张不错的图片的秩其实是比较低的,如果图像的秩比较高,往往是因为图像中的噪声比较严重。比如拍照的时候ISO感光度设置过高造成噪点太过泛滥之类的。所以,图像处理的低秩性其实可以拿来去除照片中的噪点,电影中的雨丝也可以通过低秩表达的方式来去除。
Note:低秩与稀疏。低秩是指矩阵的秩较小,稀疏是指矩阵中非零元素的个数少。如果对矩阵进行奇异值分解,并把其所有奇异值排列为一个向量,那么这个向量的稀疏性便对应于该矩阵的低秩性
我们可以利用图像的低秩性来恢复图像,首先构建融合了低秩矩阵先验的模型,再求解这个模型得到低秩的矩阵。这种基于低秩矩阵逼近(LOW-Rank Matrix Approximation,LRMA)的模型称为低秩矩阵恢复模型(LRMR)。目前,LRMR主要有鲁棒主成分分析robust PCA,RPCA)、矩阵补全(matrix completion,MC)和低秩表示(low-rank representation,LRP)等三类模式。
LRMR
假设给定数据矩阵D,D=A+E,其中A和E未知,但是A时低秩的。分别采用三种模式来求解A
鲁棒主成分分析(RPCA)
(1)经典PCA
经典的PCA来获得最优的矩阵A优化问题如下[6]:
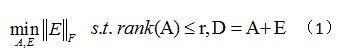 (1)
(1)
其中,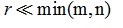 是子空间的期望维度,
是子空间的期望维度,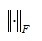 是Frobenius范数,使用PCA的前提是假设数据E元素服从独立同分布的高斯同分布。只需对矩阵D进行SVD取前r项便可得到上述优化问题的最优解。
是Frobenius范数,使用PCA的前提是假设数据E元素服从独立同分布的高斯同分布。只需对矩阵D进行SVD取前r项便可得到上述优化问题的最优解。
补充知识:F范数、奇异值分解(Singular Value Decomposition,SVD)
矩阵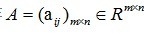 的Frobenius的范数为
的Frobenius的范数为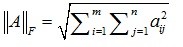
奇异值[4]:设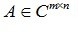 ,Rank A=r,
,Rank A=r,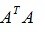 , 的特征值为
, 的特征值为
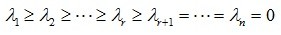
则称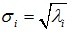 ,(i=1,2,…,r)为矩阵A的正奇异值(
,(i=1,2,…,r)为矩阵A的正奇异值( ,称为奇异值)
,称为奇异值)
矩阵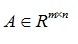 ,它的奇异值分解为
,它的奇异值分解为
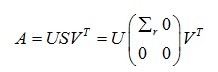
其中: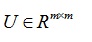 和
和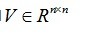 均为正交矩阵,对角矩阵
均为正交矩阵,对角矩阵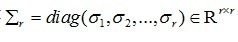 ,且其对角线元素满足
,且其对角线元素满足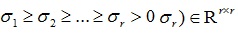 ,是A的正奇异值。
,是A的正奇异值。
物理意义[4]:奇异值分解是将矩阵分解成若干个秩一矩阵(矩阵秩为1)之和,用公式表示就是:
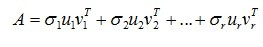
其中,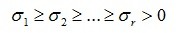 ,奇异值往往对应着矩阵中隐含的重要信息,且重要性和奇异值大小正相关。每个矩阵A都可以表示为一系列秩为1的“小矩阵”之和,而奇异值则衡量了这些“小矩阵”对于A 的权重。当我们需要存储高清图片而存储空间不够时,则可以保留奇异值较大的若干项,舍去奇异值较小的项来保证图像的可被识别精度。
,奇异值往往对应着矩阵中隐含的重要信息,且重要性和奇异值大小正相关。每个矩阵A都可以表示为一系列秩为1的“小矩阵”之和,而奇异值则衡量了这些“小矩阵”对于A 的权重。当我们需要存储高清图片而存储空间不够时,则可以保留奇异值较大的若干项,舍去奇异值较小的项来保证图像的可被识别精度。
Note:图像处理中奇异值的物理意义,参考:https://www.zhihu.com/question/22237507/answer/53804902
(2)鲁棒主成分分析
PCA在噪声较小时效果较好,当噪声较大时,即使只有很少部分的数据被干扰,也会使PCA的性能大大降低。针对该问题,Wright等人提出了鲁棒主成分分析,只要噪声矩阵E是足够稀疏的,不管大小都可以恢复出低秩矩阵A。
当E为稀疏的大噪声时,恢复矩阵A是一个双目标优化问题:
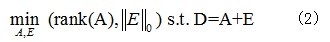
通过引入折中因子λ(>0),将双目标问题式(2)转换成如下的单目标优化问题:
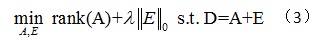
优化式(3)是NP难的,因此需要对此问题的目标函数进行松弛。将秩最小松弛为核范数的最小化,将零范数松弛为1范数,故问题式(3)松弛到如下凸优化问题[5]:
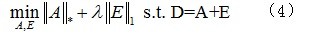
其中,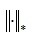 表示矩阵的核范数,即矩阵奇异值之和。
表示矩阵的核范数,即矩阵奇异值之和。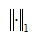 为1范数,即矩阵每个元素绝对值之和,
为1范数,即矩阵每个元素绝对值之和,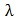 是一个正的权重参数,一般取值
是一个正的权重参数,一般取值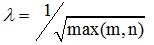 。
。
对于RPCA的求解方法主要有迭代阈值算法、加速近端梯度算法、对偶方法以及拉格朗日乘子法等,具体求解步骤参考文献[5]。
补充知识:NP难、松弛、1范数与0范数
NP难:P:算起来很快的问题
NP:算起来不一定快,但对于任何答案我们都可以快速的验证这个答案对不对
NP-hard:比所有的NP问题都难的问题
松弛(拉格朗日松弛):
首先,拉格朗日松弛技术是用在优化问题里面(假设是最小化问题),而且一定是有约束条件的优化问题。
假设我们已经知道没有约束条件的优化问题怎么解了。然后对于有约束条件的优化问题,我们想懒一点的话,就可以想想办法怎么把它转化成没有约束条件的优化问题。于是有人就想到,
1. 直接去掉约束条件!
那显然定义域变大了,那得到的最小值肯定不比原来的大。那怎么办?
2. 那就如果不满足某些约束条件,我们就来点惩罚。这个惩罚表现在目标函数上。我们在目标函数上多加一项,如果某些约束条件没有满足,那目标函数就会变大。另外我们也多了一个叫拉格朗日乘子的东西,它也是我们可以动的变量。
这时候最优的结果当然会满足所有约束条件,不然就被罚惨了。
这就是所谓的拉格朗日松弛技术,是把有约束优化问题转化成无约束优化问题的好方法
作者:知乎用户
链接:https://www.zhihu.com/question/21345731/answer/57182129
1范数与0范数
0范数为矩阵A的非零元素个数,1范数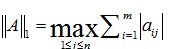
迭代阈值算法
将问题(4)正则化,便得到优化问题:
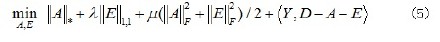
使用迭代阈值算法(iterative thresholding,IT)交替更新矩阵A、E和Y。
当 , 时,
, 时,
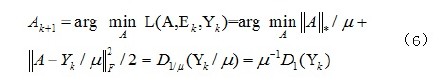
当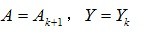 , 时,
, 时,
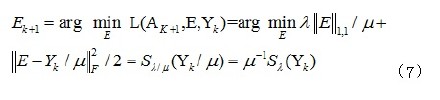
当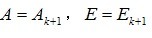 ,
,
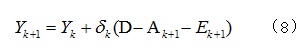
其中,
矩阵补全【5】
当数据矩阵D含丢失元素时,可根据矩阵的低秩结构来恢复矩阵的所有元素,称此过程为矩阵补全(MC)。
记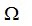 为集合
为集合 的子集,这里 [m]表示集合 {1,2,3....,m}。MC的原始模型可描述为如下的优化问题:
的子集,这里 [m]表示集合 {1,2,3....,m}。MC的原始模型可描述为如下的优化问题:
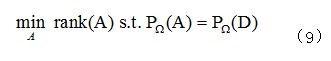
其中: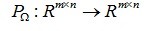 为一线行投影算子
为一线行投影算子
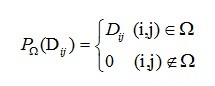
对于式(9)问题的求解参照文献[5].
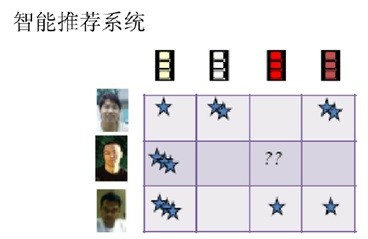

低秩表示[5]
低秩矩阵表示(LRR)是将数据集矩阵D表示成字典矩阵B(也称为基矩阵)下的线性组合,即D=BZ,并希望线性组合系数矩阵Z是低秩的。为此,需要求解下列优化问题:

含义:求解满足约束条件D=BZ下的秩最小的Z
将优化问题式(10)进行凸松弛,得到
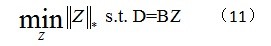
若选取数据集D本身作为字典,则有
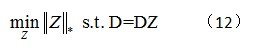
为了对噪声和野点更加鲁棒,模型扩展为

关于上式的求解参照文献[5]
补充知识:基矩阵、凸集、凸函数、凸优化问题、凸松弛
基矩阵:用矩阵形式写出基向量和基,这样的矩阵我们叫它基矩阵
i = | 1 0 0 |
j = | 0 1 0 |
k = | 0 0 1 |
B = | i | | 1 0 0 |
| j | | 0 1 0 |
| k | | 0 0 1
凸集
假设我们拥有一个集合C,从中取两个元素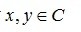 ,并有一个实数
,并有一个实数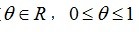 , 如果
, 如果
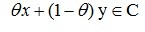
那么我们称集合C为一个凸集,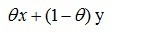 被称作x,y之间的凸连接。
被称作x,y之间的凸连接。
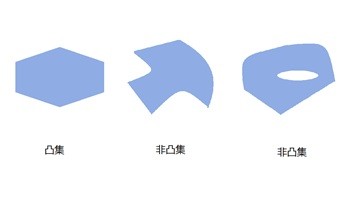
通过上述定义我们知道,如果一个集合中的任意两个点的线性组合所得到的一系列的点也在该集合中(该亮点之间的连先生的点都在该集合中),那么该集合就被称为凸集。换句话说,凸集不能有洞,不同有任何凹陷。
凸函数:
一个函数f满足
(1) 它的定义域是凸集
(2) 对于其定义域中的任意两点 对任意
对任意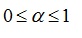
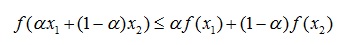
那么这个函数f就是凸函数。
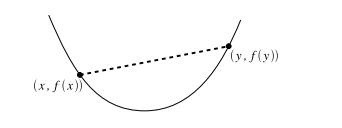
我们可以更加直观的去刻画该定义,如果一个函数是凸函数,那么该函数两点的连线必然在该函数图像的上方。
凸优化问题:
凸优化问题是一种特殊的优化问题。凸优化问题的形式是
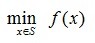
其中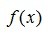 是凸函数,可行域S是凸集。此外,还有等价形式
是凸函数,可行域S是凸集。此外,还有等价形式
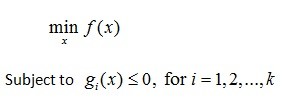
其中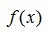 和所有的限制函数
和所有的限制函数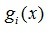 都必须是凸函数
都必须是凸函数
对于凸优化问题来说,局部最优解就是全局最优解
凸松弛:有些问题本身并不是凸的,解算起来并不方便,但是可以采用一种技术将其转换为凸函数进行解算,凸松弛就是其中一种技术。
低秩降噪
带有噪声的图像的模型如下
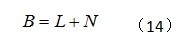
B为含噪的测量矩阵,L为待恢复的低秩矩阵,代表原始数据。N为稀疏矩阵,代表噪声。
根据RPCA的方法,可以得到图像去噪优化问题:
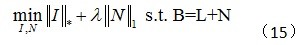
对于该问题求解,可采用迭代阈值法、对偶法、朗格朗日乘子法等进行求解。
相关知识

[1] 同济大学数学系编.工程数学 线性代数 第5版[M].高等教育出版社,2007.
[2]彭义刚,索津莉,戴琼海等.从压缩传感到低秩矩阵恢复:理论与应用[J].自动化学报,2013,39(7):981-994.
[3] 吴伟伟.基于低秩矩阵逼近的图像恢复方法研究[D],2016.
[4] 李新,何传江.矩阵理论及其应用[M].重庆大学出版社,2008.
[5] 史加荣,郑秀云,魏宗田等.低秩矩阵恢复算法综述[J].计算机应用研究,2013,30(6):1601-1605
[6] Ming,Yan,等.Exact Low-Rank Matrix Completion from Sparsely Corrupted Entries Via Adaptive Outlier Pursuit[J].Journal of Scientific Computing,2013,56(3):433-449.
这篇关于低秩恢复算法(图像去噪)_米米米米粒口红_新浪博客的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








