公交线网、地铁线网最短出行时间计算（考虑换乘耗时）

1.问题描述：

在乘坐公交或地铁时，从乘客角度出发，乘客们当然希望可以用时最短地到达目的地。出行用时不仅包括了在车时间，也包括了乘客用于换乘的时间——换乘耗时。仅将该问题视为最短路问题忽视了换乘对时间的影响，并不符合实际。因此，本文探讨在考虑换乘耗时情况下的公交、地铁线网最短出行时间、线路问题。

2.算法输入：

（1）各条线路的站点情况

（2）各站点间的用时

（3）每次换乘消耗的时间

3.算法思路：

3.1 线网重构

对线网进行重新构建，利用虚拟站点实现对换乘耗时的考虑。将换乘站点进行拆分，换乘站连接几条线路就将其拆分成几个虚拟站点，并将虚拟站点分配至对应线路上。由同一换乘站点拆分得来的虚拟站点间的用时为换乘时间。下文称重构所得线网为虚拟线网，重构后的站点称为虚拟站点，重构所得线路称为虚拟线路。

线网中的站点可以分为两类：普通站点和换乘站点

普通站点与虚拟站点一一对应，而换乘站点对应多个虚拟站点（对应数量=可换乘的线路数）

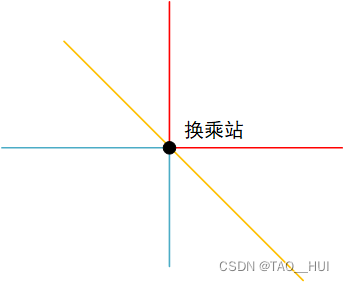
我们以一个供三条线路换乘的站点为例进行介绍，如图所示，不同颜色代表不同线路，换乘站连接了三条线路。

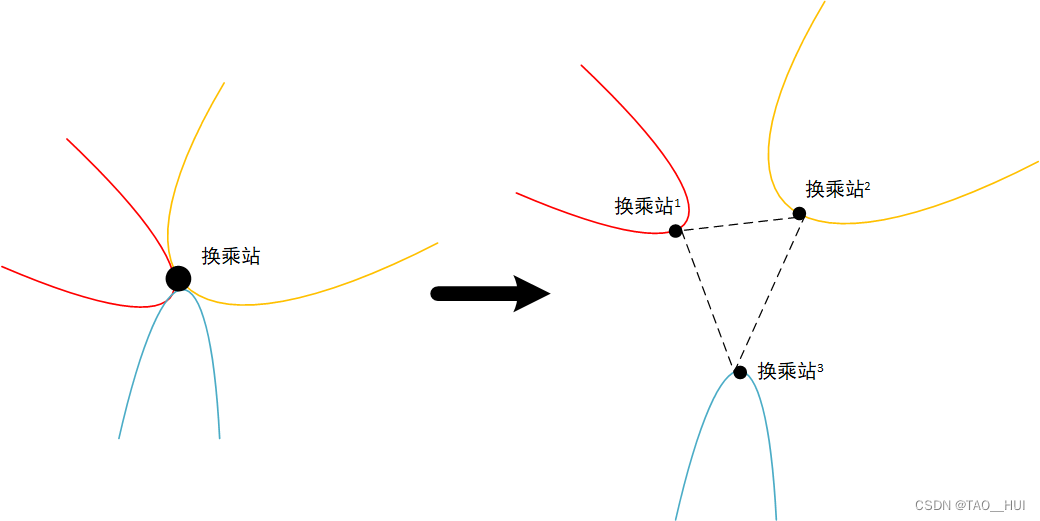
 如果只关注这一个站点，我们可以把三条线路“扭一下”，然后将换乘站拆开，三条线路通过虚拟线路进行连接换乘，也可以说虚拟线路是乘客在换乘过程中需要走动路，虚拟线路的长度（权重）即为换乘时间。

3.2 线网求解

利用Floyd法对虚拟线网进行求解，得到虚拟站点间最短距离和最短路径。

3.3 解码

将虚拟站点对应回原有的站点，获得原有站点间的最短距离和最短路径。由于虚拟线网的最短路是考虑换乘时间所得，因此对应回去后得到的最短距离已经考虑了换乘耗时。

4.具体代码示例

4.1定义一个Floyd法计算最短路的函数

    # 佛洛依德法计算最短路def floyd(adjacency_matrix):'''佛洛依德法计算最短路:param adjacency_matrix: 邻接矩阵:return: 最短距离矩阵，最短路径矩阵'''v_num = len(adjacency_matrix)shortest_dis_mat = [[x for x in row] for row in adjacency_matrix]  # 初始化最短路径矩阵# paths[i][j]记录了最短路径上节点i的后继节点编号paths = [[-1 if shortest_dis_mat[i][j] == math.inf else j for j in range(len(adjacency_matrix))]for i in range(len(adjacency_matrix))]for k in range(v_num):for i in range(v_num):for j in range(v_num):if shortest_dis_mat[i][j] > shortest_dis_mat[i][k] + shortest_dis_mat[k][j]:shortest_dis_mat[i][j] = shortest_dis_mat[i][k] + shortest_dis_mat[k][j]paths[i][j] = paths[i][k]return np.array(shortest_dis_mat), np.array(paths)