本文主要是介绍【5G NR】【一文读懂系列】移动通讯中使用的信道编解码技术-卷积码原理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、引言
二、卷积编码的发展历史
2.1 卷积码的起源
2.2 主要发展阶段
2.3 重要里程碑
三、卷积编码的基本概念
3.1 基本定义
3.2 编码器框图
3.3 编码多项式
3.4 网格图(Trellis)描述
四、MATLAB示例
一、引言
卷积编码,作为数字通信领域中的一项关键技术,自其诞生以来便受到广泛关注。卷积编码是一种纠错编码方法,它通过引入冗余信息来提高数据传输的可靠性。本文旨在全面介绍卷积编码的基本概念、原理、应用场景、优缺点等方面,并结合具体案例进行分析,以期为读者提供一个清晰、深入的卷积编码知识体系。
二、卷积编码的发展历史
2.1 卷积码的起源
卷积码,作为一种前向纠错编码技术,其历史可以追溯到20世纪50年代。当时,通信领域的研究者们正在探索如何在有限的带宽和信噪比条件下,提高数据传输的可靠性。卷积码的出现,为这一挑战提供了一种有效的解决方案。
2.2 主要发展阶段
- 早期研究阶段:在20世纪50年代末到60年代初,卷积码的概念开始形成并得到初步研究。研究者们开始探索卷积码的基本原理和性能特点,为其后续的应用奠定了基础。
- 理论成熟阶段:随着研究的深入,卷积码的理论体系逐渐成熟。在这一阶段,研究者们提出了卷积码的代数表示方法、状态转移图等关键理论工具,为卷积码的工程应用提供了理论基础。
- 工程应用阶段:从20世纪70年代开始,卷积码开始广泛应用于各种通信系统中。特别是在卫星通信、移动通信等领域,卷积码因其强大的纠错能力和较高的编码效率而备受青睐。
2.3 重要里程碑
- 1972年:Viterbi算法的出现为卷积码的高效解码提供了可能。Viterbi算法是一种最大似然解码算法,它能够在多项式时间内找到最可能的原始信息序列,从而大大提高了卷积码的解码效率。
- 1980年代:随着移动通信的快速发展,卷积码成为了第一代和第二代移动通信系统(如GSM)中的关键技术之一。在这一阶段,卷积码的优化和改进持续进行,以提高其在不同信道条件下的性能。
- 1990年代:随着第三代移动通信系统(如3G、4G)的兴起,卷积码逐渐被更为先进的编码技术(如Turbo码和LDPC码)所取代。然而,卷积码在某些特定场景(如深空通信、水下通信等)中仍具有重要地位。
三、卷积编码的基本概念
3.1 基本定义
卷积码将k个信息比特编成n个比特,特别适合以串行形式进行传输,时延小。
将卷积码记作(n,k,N)。一般来说,卷积码的k和n是比较小的整数。
- 码率仍定义为k/n。
- 卷积码是将k个比特的信息段编成n个比特的码组,其编码生成的监督码元不止和k个比特的信息段有关,还和前面的m=(N-1)个信息段有关。可知,一个监督码元同时和前m个比特以及当前输入的一个比特信息有关,即监督着N=m+1个比特,我们将N成为约束度,所有监督码元的长度nN称为约束长度。
综上,k即为卷积码的输入路数(多路输入要进行串并转换),n为输出比特个数,m为移位寄存器的位数(用于保存所需的前几个比特),N=m+1。
3.2 编码器框图
(n,k,N)=(3,1,3)卷积码编码器框图如下:
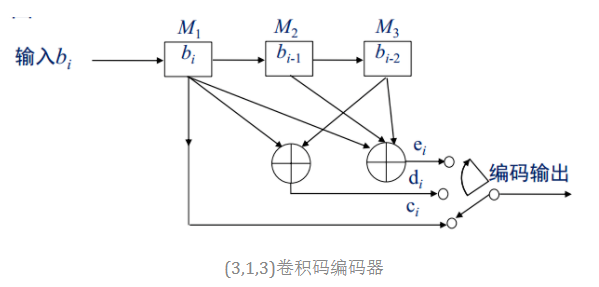
输入和输出的关系式:
(n,k,N)=(3,1,3)卷积码编码器框图如下:

输入和输出的关系式:

卷积编码的生成多项式是描述卷积编码器内部状态转移和输出码字生成的一组多项式。这些多项式通常表示为 (g(D)),其中 (D) 是一个延迟算子,表示数据在编码器中的延迟。生成多项式用于确定编码器的状态转移和输出码字的生成规则。
3.3 编码多项式
上面的编码器多项式如下:

假设输入序列x[k]=[1101],其多项式:![]() 。则输出序列y[n]:
。则输出序列y[n]:

运算符号为位异或运算。
可以得到对应输入4个比特的输出数据为:[111,110,010,100];
根据上面的编码器图和输入输出关系式,可以看出来,卷积编码是一种前向纠错编码技术,其核心思想是将待传输的信息序列与特定的编码函数进行卷积运算,生成包含冗余信息的编码序列。卷积编码的主要参数包括约束长度(N)、编码速率(k/n)和生成多项式等,这些参数决定了编码的性能和特点。
3.4 网格图(Trellis)描述
卷积码的网格图表示如下:
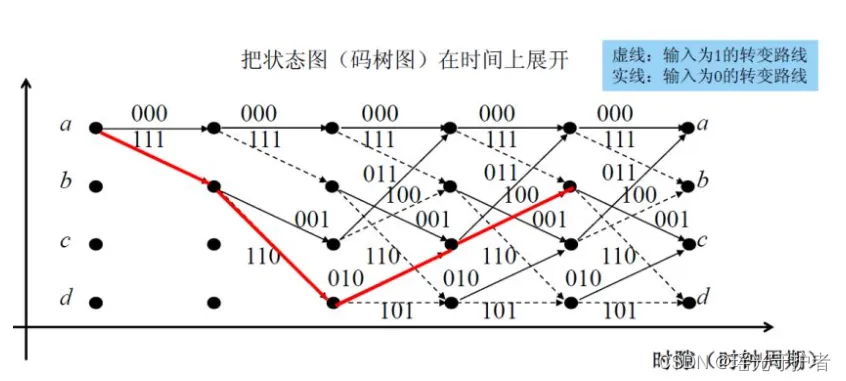
网格图显示了时序的变化,可以更为清晰的显示出编码的过程。例如当输入(1101)时,假设移位寄存器的初始状态为a状态,则编码输出如红线所示。
四、MATLAB示例
以下是一个简单的MATLAB脚本示例,演示了如何实现一个(n,k,N)=(3,1,3) 的卷积编码器:
function encoded_data = convolutionalEncoder(input_data, K, g) % 参数: % input_data - 输入数据比特流 (1xN vector) % K - 约束长度 (寄存器数量 + 1) % g - 生成多项式的矩阵形式 (Gx(K-1) matrix, G是输出数量) % 输出: % encoded_data - 编码后的数据比特流 (1x(3*N) vector for R=1/3) N = length(input_data); % 输入数据的长度 G = size(g, 1); % 输出数量 (对于R=1/3, G应为3) % 初始化寄存器状态和输出数据 register = zeros(1, K-1); encoded_data = zeros(1, N*G); % 对输入数据进行卷积编码 for i = 1:N % 构造当前寄存器的内容(包括新输入比特) register_with_input = [input_data(i) register]; % 对每个生成多项式计算输出比特 for j = 1:G % 提取对应的生成多项式 generator = g(j, :); % 计算异或和 output_bit = mod(sum(generator .* register_with_input), 2); % 将输出比特添加到编码后的数据中 encoded_data((i-1)*G + j) = output_bit; end % 更新寄存器状态 register = register_with_input(1:end-1); end
end % 示例使用
% 定义生成多项式 (通常为八进制或十六进制形式, 这里转换为二进制)
% 例如: g1 = [1 1 1], g2 = [1 0 1], g3 = [1 1 0] (八进制) g_binary = [1 0 0;1 0 1;1 1 1];% 设置约束长度 (K=4 对于上述生成多项式)
K = 3; % 输入数据比特流
input_data = [1 1 0 1 ]; % 进行卷积编码
encoded_data = convolutionalEncoder(input_data, K, g_binary); % 显示编码后的数据
disp('Encoded Data:');
disp(encoded_data);上面的程序已经通过调试,运行结果如下:
输入:
% 输入数据比特流
input_data = [1 1 0 1 ];
% 输出数据比特流
Encoded Data = [1 1 1 1 1 0 0 1 0 1 0 0];
大家可以试着运行一下,有问题可以留言。欢迎大家在评论区探讨。
这篇关于【5G NR】【一文读懂系列】移动通讯中使用的信道编解码技术-卷积码原理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




