信号完整性基础03：反射与阻抗匹配（2）

说在开头：关于x射线（1）

气体在电压作用下会发光，这个现象电学大师法拉第在1838年已经发现了，后来人们又发现靠近阳极部分的玻璃管也会发光，克鲁克斯（爱捣鼓的小伙子）打造了“克鲁克斯管”：在阳极的一端涂上荧光粉，玻璃管里面放个金属片，能在荧光粉屏幕上看到金属片的剪影，这就证明了这种射线是从阴极发射出来射向阳极的，而且射线可以被金属片挡住。

大家都觉得这玩意好玩，于是一大帮人就开始捣鼓这种现象，没过多久时间，英国人和德国人就吵了起来：德国的哥尔茨坦发现这种射线跟紫外线类似，因为紫外线也能引起荧光粉发光，所以这种射线应该是一种光。而英国物理学家瓦尔利发现阴极射线在磁场中会发生偏转，于是提出这种射线由带负电的物质微粒组成。“粒子说”得到了英国克鲁克斯和舒斯特的赞同，但德国的赫兹（不错，就是我们最熟悉的Hz，他实验验证了麦克斯韦预言的电磁波）站出来反对，他认为阴极射线是电磁波。双方都不服气，于是分头设计实验来验证各自的推测。

英国的舒斯特把带电微粒解释成：气体分子自然分解出来的碎片，带正电的部分被阴极俘获，电极间只留下带负电的部分，因而形成了阴极射线，他实验测得带电微粒的荷质比与电解所得的氢离子的荷质比数量级接近。赫兹和他的学生勒纳德也做了很多实验，他们在克鲁克斯管旁边加上电场，看看阴极射线是不是会偏转；结果侧来测去都测不到，于是赫兹说：你来看，不偏转啊，不带电没毛病，这货就是电磁波。后来赫兹和勒纳德又发现这个阴极射线居然可以穿透很薄的金属片，从0.00265mm的薄铝箔作为窗口会逸出射线，并在空气中穿行约1cm，他们更加笃定：这种射线能穿透实物，只有波才能办的到，粒子根本不可能。（参考自:吴京平-无中生有的世界）

四，传输线阻抗匹配

我们上一章讲了：传输线的目的是将信号从源端有效的传输到终端，我们希望在终端接收到的信号是完整的、可识别的。但在信号反射章节中，我们了解到要保证信号完整、有效的传输到终端，其实还真是一个技术活，从传输线的传输函数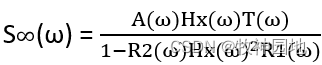：可知，源端阻抗与：A(ω)和R1(ω)有关；终端阻抗与：R2(ω)有关。

当源端阻抗与传输线特征阻抗相等，即源端串联匹配，那么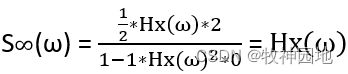：；信号从源端到终端只有传输线损耗，与源端和终端反射系数无关。

当终端阻抗与传输线特征阻抗相等，即终端并联匹配，那么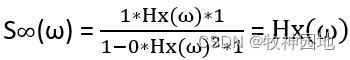：；信号从源端到终端只有传输线损耗，与源端和终端反射系数无关。

所以我们可以看到，要使信号从源端完整的传输到终端，那么有三种方式：

1. 短线模式传输函数：Sshort(ω)= ZL/(ZL+Zs)；

2. 源端匹配传输函数：S源端 = Hx(ω)；

3. 终端匹配传输函数：S终端 = A(ω)*Hx(ω)；

好，接下来我们详细分析：源端串联和终端并联这两种阻抗匹配的工作原理。

1，源端匹配

源端匹配的意思是：Zs = Z0，即源端串联电阻后使得阻抗等于传输线特征阻抗。那这样有什么好处呢？

1. 阻抗分压：A(ω) = Z0(ω)/[ Zs(ω)+Z0(ω)] = 1/2，信号从源端发出来幅度减半；

2. 假设终端负载阻抗ZL为高阻（即∞），那么可得到终端反射系数：R2(ω) = [ZL(ω)-Z0(ω)]/ [ZL(ω)+Z0(ω)] = 1，即全反射，信号幅度是输入到终端信号幅度的2倍，算上源端发出来的1/2，刚好是输出的信号幅度；

3. 源端阻抗的反射系数：R1(ω) =  [Zs(ω)-Z0(ω)]/ [Zs(ω)+Z0(ω)] = 0，即，当信号从终端反射回到源端时，信号被全部吸收；

——信号从终端反射回来后，将不会再被反射到终端去，信号传输过程结束。

4. 传输线的传输函数：S源端 = A(ω)*Hx(ω)*[ R2(ω)+1]；将A(ω)=1/2， R2(ω)=2代入传输线的传输函数；所以得到传输函数：S源端 = Hx(ω)。

——从信号的传输函数可以看到，终端接收到的信号相比于源端只是传输线本身的衰减，不会由于阻抗不连续而产生过冲等。

好，咱们再来举个栗子，如下图为源匹配各位置波形时间图：

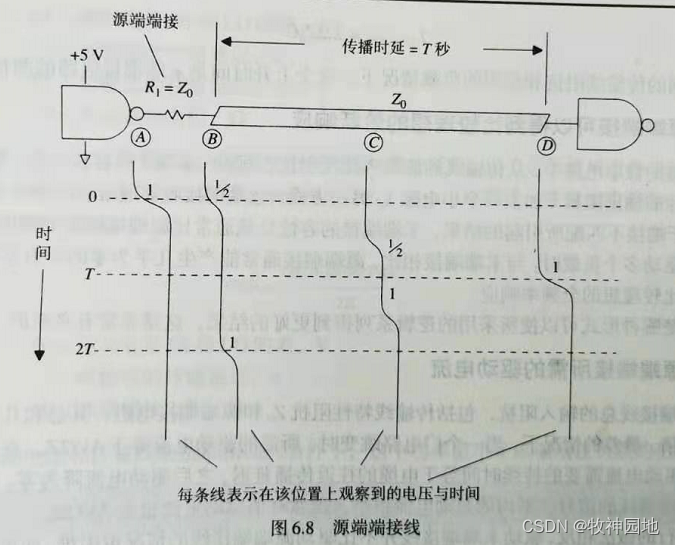
1. 当t=0时，信号从A点发出，此时A点幅值为：1；

1, 图中A点是理想驱动源：VCC或GND；A点不会受到信号分压、反射等影响，我们知道的芯片驱动内阻已合入R1中；

2, 源端匹配电阻靠近输出管脚，与驱动管脚内阻看成一体；即，从B点来看，源端匹配电阻R1 = 驱动内阻+串联匹配电阻。

——为什么串联匹配电阻和内阻能看成一个电阻呢？我上面已经提到了，如果有同学还不清楚的话，建议在好好想一想。

3, B点电压是源端匹配电阻R1与特征阻抗Z0分压，即B点幅值为：A(ω) = Z0/(R1+Z0) = 1/2。

2. 当t=T时（T为传输线传播延时）：

 1, 信号传播至终端D点，此时D点的阻抗为ZL（高阻抗），理想情况下是全反射，所以D点信号幅值为：1/2 + 1/2  = 1。

——经过时间为T的延时，终端接收到的信号是完整的信号（幅值为1），而不是一半幅值的信号。

3. 当t=2T时：

1, 从终端D点反射的1/2幅值信号传播回源端，与原先的信号叠加成完整的信号（幅值为1）；

2, 源端匹配阻抗R1，与传输线阻抗Z0相等，可得反射系数为0（无反射，全吸收），所以此时B点信号幅值为：1/2 + 1/2 = 1。

——源端发送出来的信号，经过了2T的时间后才变成完整的信号（幅值为1）。

4. C点是传输线中间位置的状态，它同样会出现台阶：靠近源端的台阶时间长，而靠近终端的台阶时间短；

1, 1驱1的电路拓扑，我们不关心传输线过程的信号状态，这些半高电平的信号并不会被采集；

2, 对于1驱N的电路拓扑，如果走线过长（产生台阶）且负载分散，那么走线中间的节点会出现半高电平（边沿不连续），需要评估接收端器件是否能可接受。

5. 源端匹配模式，是反射与叠加的完美结合，但是从源端信号（阻抗匹配B点）来看，不是完美的边沿，而是存在一个台阶，该台阶长度为2倍的传输线延时（来回反弹一次），但这对1驱1电路拓扑的传输模式不重要，要牢记：传输线的目的是使终端（接收端）信号完整；

6. 从终端向源端看的阻抗是Z0，当终端是一个容性负载（TTL/CMOS等），得到的响应类似RC低通滤波器，RC常数：RCtime=Z0*C；上升时间（10%-90%）：T10%-90%=2.2*Z0*C；

那么有一个问题是：我们是否需要等待信号传输以及反射流程全部走完（2T），才能发起下次的信号传输？如果需要等待2T时间，那么会极大的影响传输效率，数据速率将会与纯线长强相关；如果这事成真，天哪，那简直就是个晴天霹雳！

幸亏这事不存在，制约信号速率（bps）的有很多因素，却没有传输延时这一项。我们从两个方面来解释这个问题：

1. 从传输线的定义：传输线传播的只是信号的边沿，即，只有信号边沿所在位置的导线才是传输线；所以一旦信号边沿离开了源端，那么靠近源端的部分导线处于空闲状态，就可以马上发起下一次的信号传输，两者不会相互干涉；

2. 那从终端反射回来的1/2幅值信号边沿，是否会影响到下一个传输的信号呢？

1, 第二个信号与反射回的信号在相遇时会产生叠加，但是他们传播的方向不同，叠加后会相互穿越，之后还是各自保持原先的信号幅值继续传播。

——好，举个栗子：我是个打水漂高手（用碎瓦片，打出的水漂记录在40个左右），所以很喜欢往平静的池塘里扔石头；现在假象我左右手同时往池塘里扔了两块石头，然后就看到两个同心圆的水波向外荡，荡啊荡，荡啊荡，两个水波就相遇并产生了干涉：你中有我，我中有你；但神奇的是，穿越过后就发现：你还是你，我还是我，就跟两个波像是重来没有相遇过一样，各自传播开来。世间大部分的人与事莫不如是。

2，终端匹配

终端匹配目的是减小终端反射（ R2(ω)为0），那么可得到终端匹配传输函数为：S终端 = = A(ω)Hx(ω)T(ω)1-R2ωHxω2R1(ω) = A(ω)*Hx(ω)；此时信号在终端被完全吸收，不会反射到源端。

——那如何能实现终端匹配呢（（ R2(ω) = 0））？只要求ZL = Z0，就能使R2(ω) = 0；信号在第一次传输到终端后就被终结掉了，不会再反馈回到源端。

1，终端并联匹配

并联匹配如下图所示有如下特点：

1. 假设源端输出阻抗很小(Zs≈0，A(ω)≈1),那么在传输线上是全幅值传播；

——源端串联匹配的第一次传输是半幅值，但若Zs很小时，第一次传输的信号基本上就是全幅值。

2. 所有反射波形在终端被并联匹配电阻抑制（R1=Z0）；

——如上分析，当线路阻抗匹配时，则不会产生反射。

3. 接收端电压 = 发送端电压，只有传输线延时。

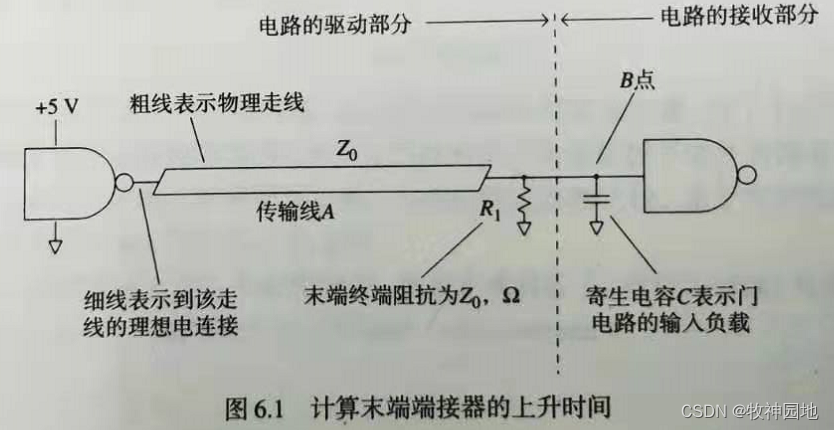
上图中输入端管脚等效成寄生电容C，那么电路的时间常数RCtime = （Z0 | R1）*C = (Z0/2)* C，计算RC滤波上升时间（10%-90%）公式：Tterm = 2.2*(Z0/2)*C = 1.1*Z0*C。假设信号发出原上升沿时间为：T1，那么B点（芯片管脚内部）的实际上升延（10%-90%）时间：TB= √T²term+T²1。

——充放电时间是源端匹配的一半，边沿时间比源端匹配快，但并不能快一倍。

从上述分析，终端并联匹配的信号传输模型更简单，传输线上所有位置的信号相等（不会出现半高电平），同时传输线充电常数比源端匹配小一半，简直就是完美的匹配拓扑。但为什么我们在实际应用中，却使用源端匹配更多呢？

让我们来做一个简单的算术题：假设输出LVTTL电平（3.3V），传输线阻抗为50ohm，所以需要在终端匹配：50ohm电阻至GND；那么在输出3.3V高电平时，在50ohm电阻上流过的电流是：3.3V/50 = 66mA，且终端匹配电阻上消耗功率P = 3.3 *0.066= 0.22W；这将导致如下3个问题：

1. TTL/CMOS管脚输出电流一般支持不了66mA，输出端芯片负载太大；

2. 如果选用陶瓷贴片电阻，则至少需要1206以上封装；

3. 一个信号线匹配需要0.22W，那么100个信号线匹配就要会浪费22W无用损耗。

2，终端戴维南匹配

这么好的匹配拓扑，实在弃之可惜；所以我们一般会采用改进版本：戴维南匹配（分离式端接匹配），如下图所示； R1和R2电阻比值控制着高低电平驱动电流的相对比例，而且R1和R2电阻值的选择，有三个约束条件：

1. R1和R2并联阻值等于Z0；

2. 输出电流不能大于Iohmax（最大高电平输出电流）；

3. 输出电流不能大于Iolmax（最大低电平输出电流）。

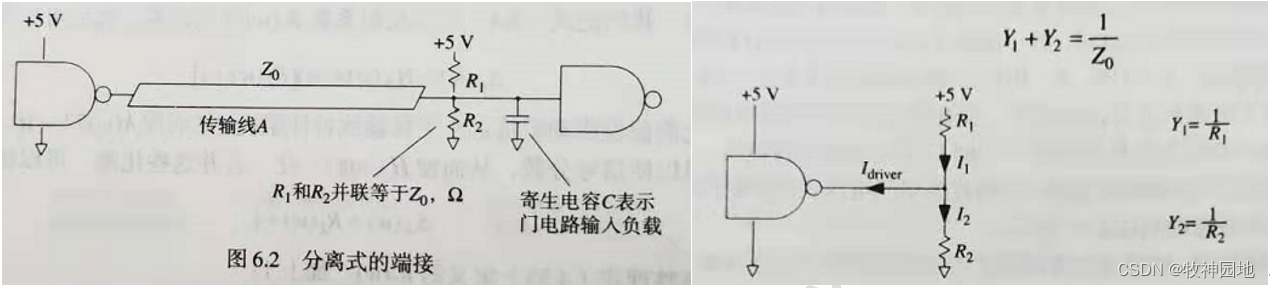
举个栗子：我们常见的DDR的ADDR/CMD线匹配，是戴维南终端匹配；可以从VDDQ电源电压分压终端端接，也可以通过VTT电源电压直接端接到ADDR/CMD上。

五，传输线拓扑

从上面的分析中，我们能够很清晰的看到源端串联匹配和终端并联匹配的优缺点，我们再来所一个总结；

1. 源端串联匹配特点：

1, 传输线拓扑损耗（匹配电阻损耗）相对并联匹配较小，直流电压无损耗；

2, 传输线最末端的信号是最好的，随着距离末端越远，信号边沿的台阶越明显。

2. 源端串联匹配应用场景：

1, 1驱1传输线拓扑；

2, 1驱N传输线拓扑，走线延时相对信号边沿较短，或则终端负载集中在传输线的末端，其反射信号不足以到之后信号边沿出现明显的台阶；

3, 1驱N传输线拓扑，走线很长，信号速率很低，边沿就算出现较明显的边沿，也不会影响数据的传输；例如：IIC。

3. 终端并联匹配特点：

1, 传输线拓扑损耗（匹配电阻损耗）大；

2, 传输线所有位置的信号等于输出端信号，传输线上不存在反射；

3, 信号上升RC充电延时相对较小；

4, 终端并联匹配电阻必须放在传输线的末端。

4. 终端并联匹配应用场景：

1, 适用1驱N传输线拓扑，信号速率高、摆幅低（较小损耗），对负载分布无要求，适用于单向1驱N的信号；例如：DDR总线ADDR/CMD信号；

2, 差分信号（后面章节具体分析）。

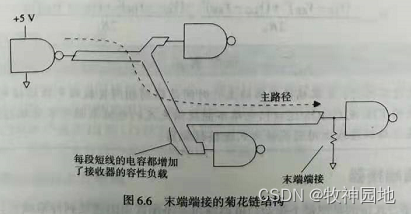
在实际应用中使用源端串联匹配还是终端并联匹配，往往不能一概而论，需要根据实际情况具体分析，通过SI仿真工具是一个非常好的途径。

写在最后

本章我们从传输线的基础概念继续延伸，研究单根传输线的信号传输过程和原理：

1. 存在反射就一定不好么？

2. 匹配就一定是完美的么？

3. 那么我们既在源端串联匹配又在终端并联匹配，信号是否就能更好呢？

基于传输线反射的理论，我们还是要回到传输线本身的定义：如何保证信号从源端出发经过传输线后被有效/完整的传输到终端。

本章部分相关内容和图片参考自：Eric Bogatin-《信号完整性分析》；霍华德.约翰逊-《高速数字设计》。下一章《串扰》。