【数据结构初阶-复杂度】运行 只用了3ms...我真牛（得意

前言

本期是我们第一次真正意义上学习数据结构，一起看看吧~

1.数据结构与算法

1.1 数据结构

：计算机存储、组织数据的方式，这些数据间存在特定关系，同时又构成集合。

简单来说

数据结构是在内存中管理数据。

1.2 算法

：将 未处理数据 处理成 已处理数据。

很简略地说，算法就是 “处理”。

那么如何衡量算法的好坏呢？

同一件事，交给不同的人处理有不同的效果；同一堆数据，交给不同的算法处理也有不同的效率。

要衡量算法的好坏，前辈们引入了复杂度的概念…

2.复杂度

处理一堆数据：执行代码需要时间；实现算法需要空间

于是有了 时间复杂度 和 空间复杂度

怎么表达复杂度呢？上机测试运行时间？精准观察内存情况？

有 不同机器运行速度不一样 等等干扰，这样做显然不现实，前辈们就想到：用函数来表示复杂度

2.1 复杂度的表示

大O符号（Big O notation）：表示函数的渐近行为

有了它，既可以描述算法复杂度大致情况，也不繁琐

前面说到用函数表示复杂度，就有了这些表示…

• O( 1 )
• O( N )
• O( N^2)
• …

这些函数，也通常叫做大O阶

也称这种表示法为，大O渐近表示法

大O函数里边的 N 是怎么得来的呢？

慢慢往下看吧~

2.2 时间复杂度

：用来衡量算法执行的快慢

算法执行的快慢，能够用时间来衡量吗？不能，机器不同，速度不同，我的程序只跑了3ms也可能只是因为，我是装备哥。

那如何衡量算法快慢？

语句的执行次数，不管什么机器，语句的执行次数越多，执行耗费时间也越多。

所以

算法中基本操作的执行次数，才能表示算法的时间复杂度

我们来看个例子：

请问 cnt++； 这条语句执行了多少次？

int cnt = 0;void f1(int n)
{int i = 0;for (i = 0; i < n; i++){int j = 0;for (j = 0; j < n; j++){cnt++;}}
}void f2(int n)
{int i = 0;for (i = 0; i < 2 * n; i++){cnt++;}
}int m = 20;void f3(int m)
{while (m--){cnt++;}
}int main()
{f1(n);f2(n);f3(m);return 0;
}

• f1(n)：用n控制的两层for循环——n^2次
• f2(n)：用2*n控制的一层for循环——2*n次
• f3(m)：m是10，while用m- -控制——10次
• 总共：n^2 + 2*n + m次

所以复杂度写出来是 O(n^2 + 2*n + m)…吗？

我们提到大O符号是表示函数渐近的，函数渐近的真正含义是什么呢？照我理解，是 N 趋近无穷

：

• 对于 n^2 ，2*n 是弟弟
• n 和 2*n 也没啥区别
• 常数更是弟弟
• …

2.2.1 大O阶的推导

其实这也体现了大O函数的推导方法：

• 用常数1取代括号内所有加法常数
• 括号内只保留最高阶的项
• 如果最高阶的项存在，而且不是1，就去掉其系数

用大O阶来表示上面程序的时间复杂度，是 O(n^2)

2.2.2 常见的时间复杂度

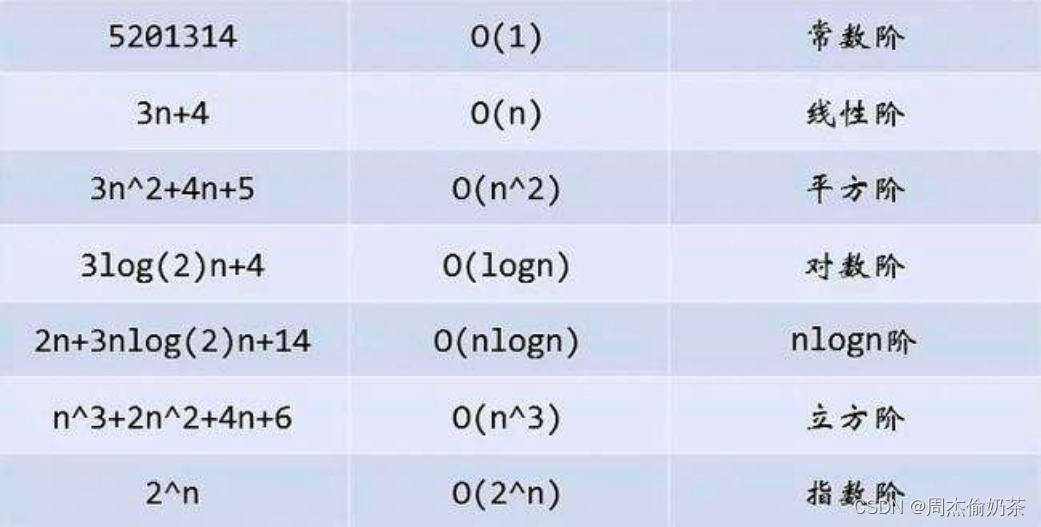
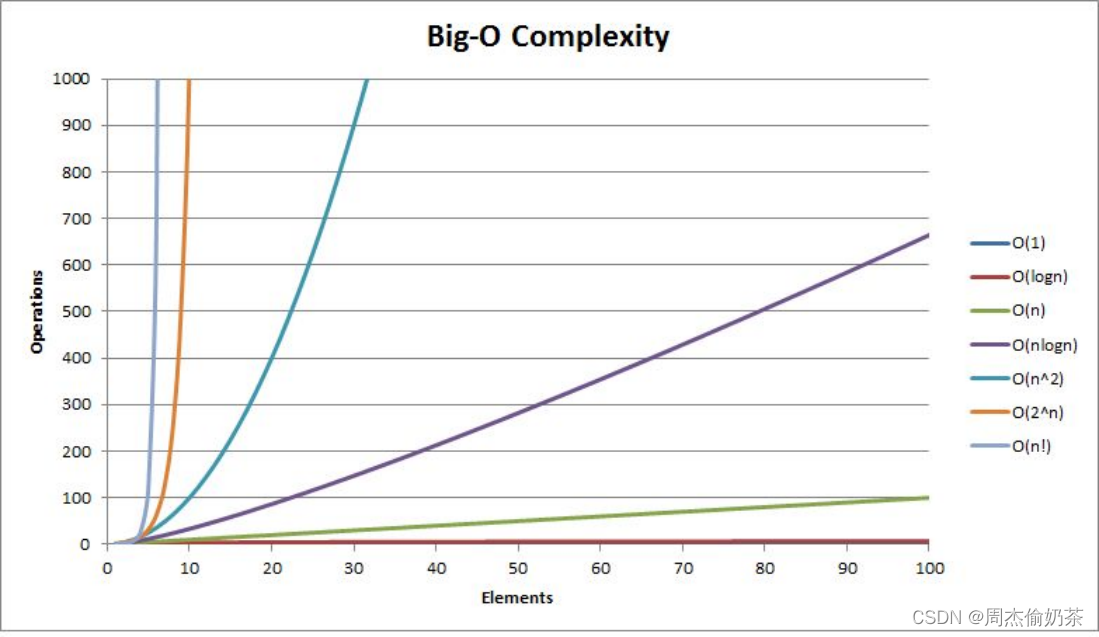
2.2.3 最坏情况

关于计算时间复杂度，除了大O，还有一个准则：

对于算法，一般关注它的最坏运行情况；个别算法根据特性会关注不同的运行情况：平均、最坏

比如 希尔排序就关注平均情况，因为很少出现最坏情况

说高大上点就叫预期管理，哈哈哈哈哈

有这么一个算法，复杂度最坏是 O(n^2) ，平常是O(n)，告诉你复杂度是O(n^2)

你拿到程序跑了跑，O(n)，哟，还挺快；碰巧遇到最坏情况，O(n^2)，“嗯…确实是O(n^2)的复杂度”

2.2.4 实例演练

上几个例子，算算它们的时间复杂度

例1

void f1(int n)
{int count = 0;for (int k = 0; k < 2 * n ; ++ k){++count;}int m = 10;while (m--){++count;}printf("%d\n", count);
}

• 第一个for循环用 2*n 控制，执行次数随着 n 的增加，是n^2次
• 第二个循环是用常量 m 控制，执行10次，常数次
• 则 f1(int n) 的时间复杂度是 O(n^2)——常数次是弟弟

例2

void f2(int n, int m) 
{int count = 0;for (int k = 0; k < m; ++ k){++count;}for (int k = 0; k < n ; ++ k){++count;}printf("%d\n", count);
}

• 第一个for循环用 m 控制，随着m的增加，执行m次
• 第二个for循环用 n 控制，随着n的增加，执行n次
• 则f2(int n)的时间复杂度为 O(m+n)

例3

void BubbleSort(int* a, int n) 
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

• 第一层for循环用n控制，随着n的增加循环体执行n次
• 第二层for循环用end控制，随着n的增加，循环体执行 1+2+3+…+(n-2)+(n-1) 次，是等差数列，n*(n-1)*1/2，即 n^2 次
• 则BubbleSort的时间复杂度是 O(n^2)——第一层的n和第二层的n^2比起来是弟弟
• *有意思的是，我们加了一个判断是否有序的优化，所以BubbleSort的最好情况是O(n)——用n次遍历数组

例3

const char * strchr ( const char * str, int character );

strc的功能是在字符串中查找字符

• 最好情况：只需要常数次就能找到，O(1)

• 平均情况：需要 n/2 次才能找到，O(n/2)

• 最坏情况：需要 n 次才能找到，O(n)

• 此算法的特性不特殊，关注最坏情况：时间复杂度是O(n)

练习到这里，很多伙伴可能感受到规律了，其实就是看控制循环的变量嘛！n/m对应O(n)/O(m)；100对应O(1)…

但真的是这么简单吗？其实不然，执行次数并不只由控制循环的变量决定，还牵扯到 算法的逻辑

看看下面的二分查找就知道了

例4

int BinarySearch(int* a, int n, int x)
{assert(a);int left = 0;int right = n-1;// [begin, end]：begin和end是左闭右闭区间，因此有=号while (left <= right){int mid = left + ((right-left)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1; 
}

while循环用left和right控制，随着n的增加，查找的范围不断变化： n /2 /2 /… /2 /2，最后范围缩到只有一个数。也就是每查找一次范围/2，最终到1

• 假设查找了x次，n /2 /2 /… /2 /2 = 1 --> n = 1*2^x = 2^x --> x =
  $$O(lo{g}_{2}n)$$

• 在复杂度的计算中，我们常把底数2省略

• 则二分查找算法的时间复杂度是
  $$O(lo{g}_n)$$

例3

const char * strchr ( const char * str, int character );		

*strchr 是用来查找字符串中的字符既然是查找，也能分情况了

• 最好情况：O(1)
• 平均情况：O(n/2)
• 最坏情况：O(n)
• 时间复杂度：O(n)

例4

long long Fac(size_t n) 
{if (1 == n)return 1;return Fac(n - 1) * n;

• n！ = 1*2*3*…*n
• n增大，递归次数随之增多，每次调用只执行常数次代码
• 则时间复杂度为O(n)

那如果是这样呢？

long long Fac(size_t n) 
{size_t M = n;while (M--){printf("%d ", n);}if (1 == n)return 1;return Fac(n - 1) * n;
}

• n增大，调用次数随之增多，每次调用执行n次代码
• 则时间复杂度为O(n^2)

例5

long long Fib(size_t n)
{if (n < 3)return 1;return Fib(n - 1) + Fib(n - 2);
}

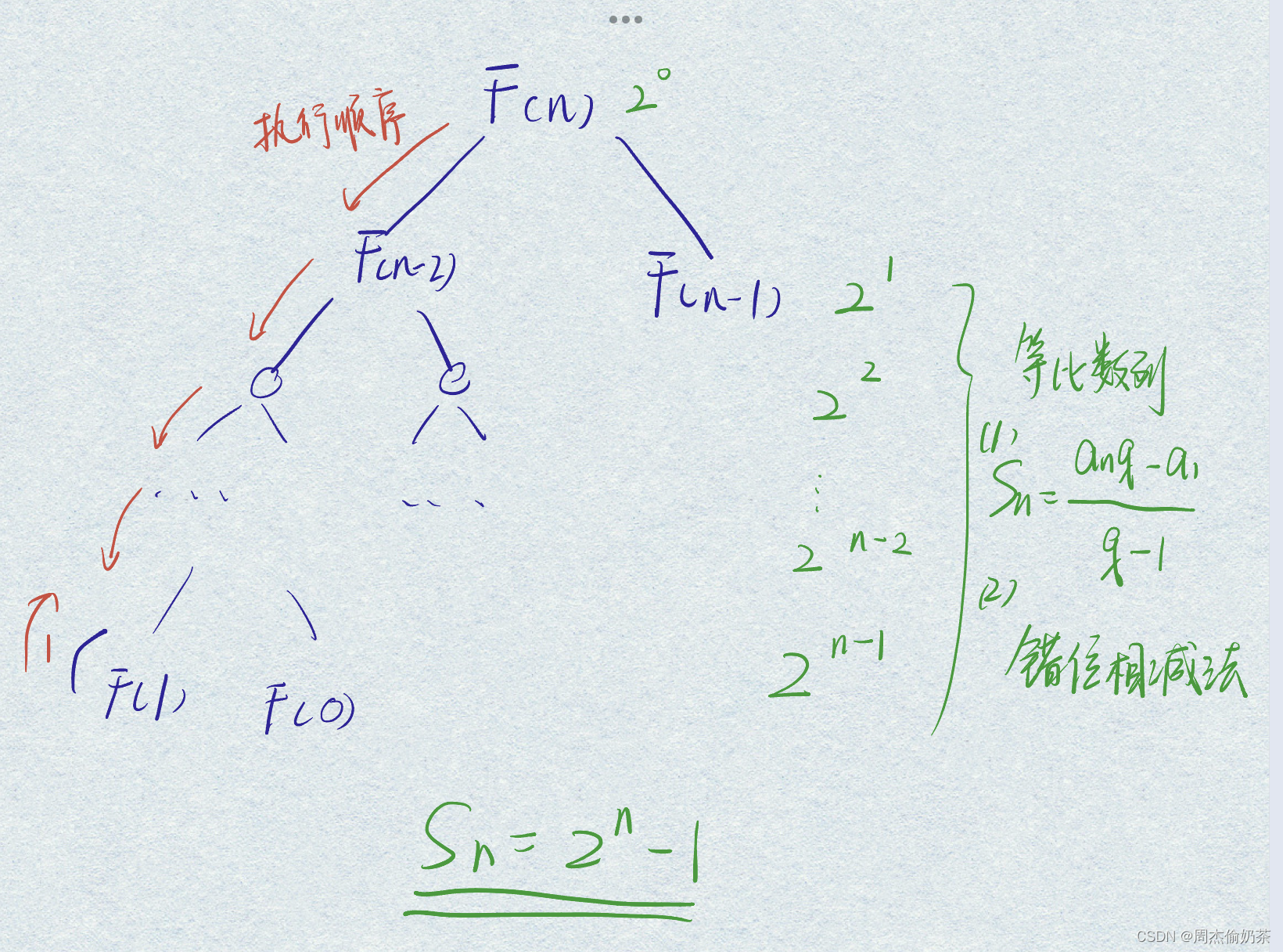
• 可以看到，函数的递归次数是 2^0 + 2^1 + … + 2^{(n-1)，等比数列求前n项和，算出来是2}n - 1

• 时间复杂度为 O(2^n)

这个复杂度也太高了，n给大点都没法用了，看不下去，来优化一下

//迭代版Fib
long long Fib(size_t n)
{long long f1 = 1, f2 = 1, f3;size_t i = 0;for (i = 3; i <= n; i++){//求第i个斐波那契数f3 = f1 + f2;//迭代f1 = f2;f2 = f3;}return f3;
}

• 只用执行n-3次循环体
• 则时间复杂度为O(n)

2.4 空间复杂度

：用来衡量算法执行需要的空间

有一点我们需要了解：时间无法重复利用；空间可以重复利用

也就是说

开辟+释放 或者是 申请+销毁 == 没有用额外的空间

• 代码块内申请的空间基本都不是额外空间——除了代码块就销毁了，比如 函数调用、循环

有了上面的基础，可以更好地引入：

额外申请的空间才能表示空间复杂度

2.4.1 实例演练

例子1

void BubbleSort(int* a, int n) 
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

循环的空间使用

end只创建了一次没毛病，但是 exchange 和 i 是不是都重复创建了？

是重复创建了，但是仔细看它们的位置，都在小代码块内——出了花括号就销毁了 ，创建销毁-创建销毁…一直在重复利用同一块空间

• end、exchange、i ：常数个变量
• 所以空间复杂度是 O(1)

总结：循环内的空间不断刷新，空间也不断复用

例子2

long long Fib(size_t n)
{if (n < 3)return 1;return Fib(n - 1) + Fib(n - 2);
}

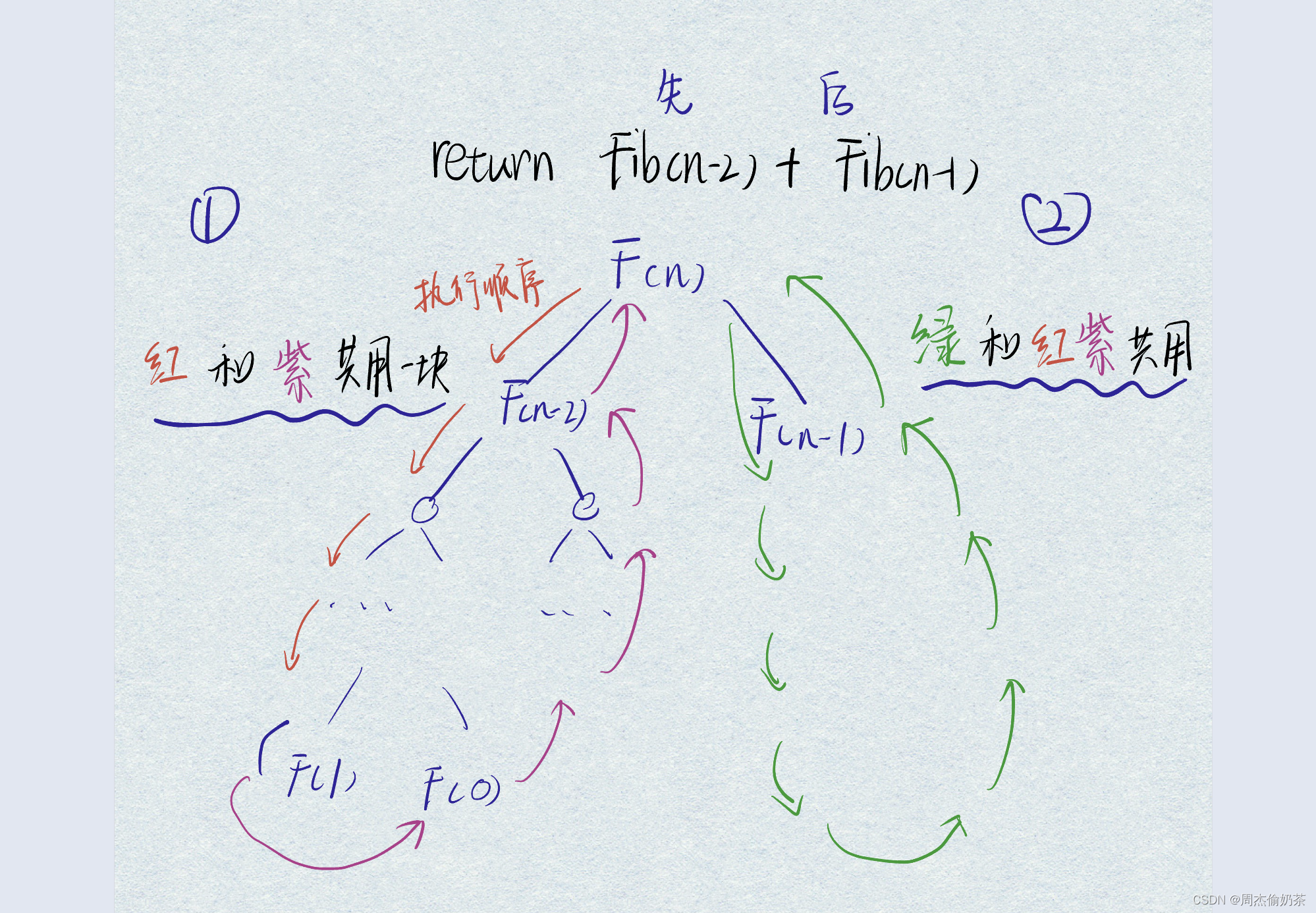
函数的空间使用：

递归函数的栈帧不是同时运行的，从左到右先后开辟，左边运行完销毁了，才给右边开辟空间来运行

这样一来，红色栈帧运行完，才轮到紫色；此时红色栈帧已经销毁，紫色就在原来红色栈帧的内存空间开辟栈帧；同理，紫色销毁后，绿色又先后在红色和紫色原来的内存空间开辟栈帧。来来回回都在红色的空间（同一块空间）上调用

• 最左边红色的函数调用，从Fib(n) 到 Fib(1) ，一共调用了 n-1次，后面的调用都在复用空间

• 则递归版本的Fib的空间复杂度是 O(n)

总结：函数栈帧用完就销毁，常常复用同一块空间创造函数栈帧

---

本期分享就到这啦，不足之处望请斧正

培根的blog，和你共同进步！