剑指offer：Python 剪绳子 动态规划和贪心

本文主要是介绍剑指offer：Python 剪绳子 动态规划和贪心，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

给你一根长度为n的绳子，请把绳子剪成整数长的m段（m、n都是整数，n>1并且m>1），每段绳子的长度记为k[0],k[1],…,k[m]。请问k[0]xk[1]x…xk[m]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

思路及Python实现

思路一：动态规划

• 先自上而下分析，在长度为n的绳子所求为f(n)，剪下一刀后剩下的两段长度是 i 和 n-i，在这个上面还可能继续减(子问题)，所以有：
  
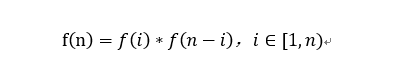
• 然后自下而上的解决问题，可以从f(1)开始向上计算并保存，最终获得f(n)的值。
  由于当i大于n//2时，就不用在计算了，重复计算因此实际上:
  

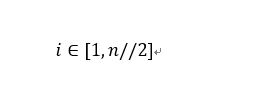
class Solution:def cutRope(self, number):if number < 2: return 0if number == 2:return 1if number == 3:return 2products = [0, 1, 2, 3]for i in range(4, number+1, 1):product = 0for j in range(1,4//2+1,1):res = products[j]* products[i-j]product = max(res,product)products.append(product)return  products[-1]

贪心算法

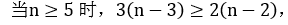
• 等号在n=5时成立，所以应把绳子剪成尽量多的3，让剩下的都是2这样的组合；尽量把大于5的数分解成3的乘积，如果剩下的长度为4，则把4分解成2和2，因为3\times× 1 < 2 \times× 2

class Solution:def cutRope(self, number):if number < 2: return 0if number == 2:return 1if number == 3:return 2timesof3 = number // 3if number - timesof3 * 3 == 1:timesof3 -= 1timesof2 = (number - timesof3 * 3) / 2return (3**timesof3)*(2**timesof2)

2019.12.15 刷完

这篇关于剑指offer：Python 剪绳子 动态规划和贪心的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---