(NYoj 110) 剑客决斗 --DP

2024-02-05 02:48

文章标签 dp nyoj 110 剑客决斗

本文主要是介绍(NYoj 110) 剑客决斗 --DP，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

剑客决斗
时间限制：5000 ms | 内存限制：65535 KB
难度：5
描述
在路易十三和红衣主教黎塞留当权的时代，发生了一场决斗。n个人站成一个圈，依次抽签。抽中的人和他右边的人决斗，负者出圈。这场决斗的最终结果关键取决于决斗的顺序。现书籍任意两决斗中谁能胜出的信息，但“A赢了B”这种关系没有传递性。例如，A比B强，B比C强，C比A强。如果A和B先决斗，C最终会赢，但如果B和C决斗在先，则最后A会赢。显然，他们三人中的第一场决斗直接影响最终结果。

假设现在n个人围成一个圈，按顺序编上编号1~n。一共进行n-1场决斗。第一场，其中一人（设i号）和他右边的人（即i+1号，若i=n，其右边人则为1号）。负者被淘汰出圈外，由他旁边的人补上他的位置。已知n个人之间的强弱关系（即任意两个人之间输赢关系）。如果存在一种抽签方式使第k个人可能胜出，则我们说第k人有可能胜出，我们的任务是根据n个人的强弱关系，判断可能胜出的人数。

输入
第一行是一个整数N(1<=N<=20)表示测试数据的组数。
第二行是一个整数n表示决斗的总人数。(2<=n<=500)
随后的n行是一个n行n列的矩阵，矩阵中的第i行第j列如果为1表示第i个人与第j个人决斗时第i个人会胜出，为0则表示第i个人与第j个人决斗时第i个人会失败。
输出
对于每组测试数据，输出可能胜出的人数，每组输出占一行
样例输入
1
3
0 1 0
0 0 1
1 0 0
样例输出
3
来源
《世界大学生程序设计竞赛高级教程·第一册》

分析：
考虑 x 是否能赢得战斗，把环看成链，x点拆成两个，分别作为链的起点和终点。
这样，则 x 能从所有人中胜出的充要条件就是 x 能与自己“相遇”。
设meet[i,j] 记录 i 和 j 能否相遇，能则为true，否则为false。（i 和 j 为上述提到的链的起点和终点）
在一个环中，相邻的两个人是可以相遇的，所以初始时meet[i][i+1]=true;
则问题转化成了是否能在i,j之间找到一个k,使得 i 和 k ， k 和 j 均能相遇，且 i 或者 j 能打败 k （i能打败k则i打败k后可以与j相遇；由于k,j相邻，所以k,j之间可以产生决斗，当j打败k后i,j也相遇了）。
状态转移方程： meet[i][j]=meet[i][k] && meet[k][j] && (beat[i][k] || beat[j][k]);
如：
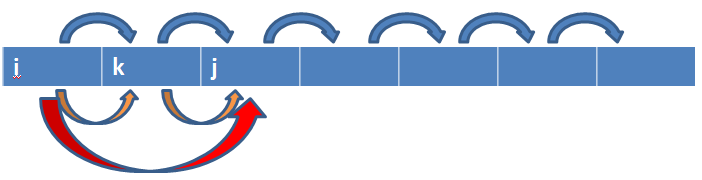
这里写图片描述
开始时距离为一的都可以相遇，我们将所有距离为2的i,j进行上式的转换，那么一次循环之后，满足条件的所有距离为2的也可以相遇了。依次类推，我们可以将所有的可相遇情况更新出来。

AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;const int N = 510;
bool beat[N][N],meet[N][N];int main()
{int t,n;scanf("%d",&t);while(t--){scanf("%d",&n);for(int i=0;i<n;i++)for(int j=0;j<n;j++)scanf("%d",&beat[i][j]);memset(meet,false,sizeof(meet));for(int i=0;i<n-1;i++) meet[i][i+1]=true;meet[n-1][0]=true;for(int d=2;d<=n;d++){for(int i=0;i<n;i++){int j=i+d;for(int k=i+1;k<j;k++){if(meet[i][k%n] && meet[k%n][j%n] && (beat[i][k%n] || beat[j%n][k%n])){meet[i][j%n]=true;break;//只要满足依次即可提前中断}}}}int ans=0;for(int i=0;i<n;i++)if(meet[i][i]) ans++;printf("%d\n",ans);}return 0;
}