本文主要是介绍P1219 [USACO1.5]八皇后 Checker Challenge(DFS回溯),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一个如下的 6 \times 66×6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。

上面的布局可以用序列 2\ 4\ 6\ 1\ 3\ 52 4 6 1 3 5 来描述,第 ii 个数字表示在第 ii 行的相应位置有一个棋子,如下:
行号 1\ 2\ 3\ 4\ 5\ 61 2 3 4 5 6
列号 2\ 4\ 6\ 1\ 3\ 52 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 33 个解。最后一行是解的总个数。
输入格式
一行一个正整数 nn,表示棋盘是 n \times nn×n 大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
输入输出样例
输入 #1
6输出 #1复制
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4说明/提示
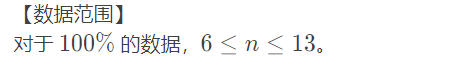
错解:
自己写了个DFS,最后一个测试点超时。。。
#include<bits/stdc++.h>
using namespace std;
int n;
int dx[]= {-1,1,0,0,1,1,-1,-1};
int dy[]= {0,0,-1,1,1,-1,1,-1};
int vis[20][20];
int f;
bool fun(int x,int y,int op)
{while(x>=1&&x<=n&&y>=1&&y<=n){if(vis[x][y]==1)return false;x+=dx[op],y+=dy[op];}return true;
}
bool check(int x,int y)
{bool flag = true;for(int i = 0; i<8; i++){int ax = x+dx[i];int ay = y+dy[i];flag = fun(ax,ay,i);if(flag == false)return false;}return true;
}
int step[20];
long long ans;
void dfs(int x,int num)
{if(num==n){if(ans<3){for(int i = 0;i<n;i++){if(i==0)cout<<step[i];else cout<<" "<<step[i];}cout<<endl;}ans++;return ;}for(int i = 1; i<=n; i++){if(check(x,i)){vis[x][i]=1;step[num]=i;dfs(x+1,num+1);vis[x][i]=0;}}
}
int main()
{cin>>n;dfs(1,0);cout<<ans<<endl;
}
正解:
分析:要放一个棋子时没必要递归去判断三行三列以及两条对角线上是否有棋子,只需要利用初中知识。。。
开三个数组(其实应该是行一个,列一个,两条斜线两个,但是因为我们是一行一行去枚举的,所以已经保证了每行有一个,因此只需要开三个数组即可),分别为col[N],l[2*N],r[2*N]
斜线怎么表示呢?

只要在斜线上,b=X+Y,X和Y可以看作是棋子的横坐标和Y的纵坐标。

只要在这一条斜线上就一定满足,b = X-Y,此时b可能为负值,但是没关系,只需要加一个N即可保证b是正数。
#include<cstdio>
using namespace std;
int n,sum;
bool col[20],u[40],v[40];
int a[20];
void dfs(int x)
{if(x>n){sum++;if(sum<=3){for(int i=1;i<=n;i++)printf("%d ",a[i]);printf("\n"); }return;}for(int i=1;i<=n;i++){ if(!col[i]&&!u[x+i]&&!v[x-i+n]){col[i]=1;u[x+i]=1;v[x-i+n]=1;a[x]=i;dfs(x+1);col[i]=0;u[x+i]=0;v[x-i+n]=0;}}
}
int main()
{scanf("%d",&n);dfs(1);printf("%d",sum);return 0;
}
这篇关于P1219 [USACO1.5]八皇后 Checker Challenge(DFS回溯)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




