本文主要是介绍平衡树学习(2)——Splay,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Splay是一种平衡树,它的代码复杂度和时间复杂度稍弱于Treap,但由于其可以支持区间操作,所以在实战中还是有许多用处。
我们先来看看Splay的定义和基本思路。
伸展树(Splay Tree),也叫分裂树,它能在O(log n)内完成插入、查找和删除操作。在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
它的优势在于不需要记录用于平衡树的冗余信息。
Ps:我们介绍的Splay是双旋操作Splay。
数组定义:
struct node{int fa,siz,ct,val,son[2];
}T[MAXN];
//fa记录父亲节点,siz记录子树大小,val记录当前节点值,ct表示与当
//前节点值相同的点个数,son[2]记录其左儿子和右儿子。
预先操作:
1.clear:清空点k里的数据
void clear(int k){T[k].siz=T[k].ct=T[k].fa=T[k].val=T[k].son[0]=T[k].son[1]=0;
}
2.up:统计k的子树大小
void up(int k){T[k].siz=T[L].siz+T[R].siz+T[k].ct;
}
3.get:查询k是父亲的左儿子还是右儿子
int get(int k){return T[T[k].fa].son[1]==k;
}
旋转:
对于Splay来说,最重要的就是rotate旋转和splay伸展操作。
对于rotate操作,我们可以类比于Treap的旋转。
void rotate(int &k){int fa=T[k].fa,gran=T[fa].fa;int d1=get(k),d2=get(fa);T[T[k].son[d1^1]].fa=fa;T[fa].son[d1]=T[k].son[d1^1];T[k].son[d1^1]=fa;T[k].fa=gran;T[fa].fa=k;if(gran) T[gran].son[d2]=k;;up(fa);up(k);
}
splay操作是Rotate的升级版,该函数将子节点旋转到根,来保持Splay的复杂度。
每次的splay操作,我们都将其旋转到根节点。对于Splay的伸展操作,我们需要进行讨论:
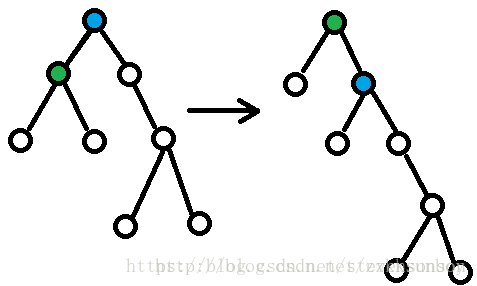
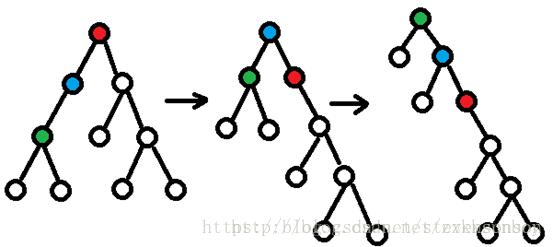
1.当旋转的点中有根节点时,可以直接进行旋转。
2.当点x和其父亲,祖父三点共线,则先旋转x的父亲,然后旋转x。
3.如果x和其父亲,祖父三点不共线,旋转两次x。
void splay(int k){for(int fa;fa=T[k].fa;rotate(k))if(T[fa].fa) rotate(get(fa)==get(k)?fa:k);root=k;
}
删除:
删除操作需要进行讨论,如果对于值x存在多个,那直接将x所在节点k的size和ct减1即可。如果不是这样,我们继续讨论,如果k没有儿子,直接clear节点k即可。如果k只有一个儿子,就将它的儿子接上来即可。如果k有两个儿子,就将它的前驱接到它父亲上,然后将k的右儿子接到前驱上,这样就删去了k节点。
int find(int k,int val){ //先求出要删除点的位置,并进行splay伸展if(!k) return 0;if(val==T[k].val){splay(k);return k;}return find(T[k].son[val>T[k].val],val);
}
void delet(int x){int pl=find(root,x);if(!pl) return;if(T[root].ct>1){T[root].ct--,T[root].siz--;return;}if(!T[root].son[1]&&!T[root].son[0]){clear(root),root=0;return;}if(!T[root].son[1]||!T[root].son[0]){int rt=root;root=T[root].son[0]+T[root].son[1];T[root].fa=0;clear(rt);return;}int rt=root;pre(root,x);splay(dist);T[T[rt].son[1]].fa=root;T[root].son[1]=T[rt].son[1];clear(rt);up(root);T[root].fa=0;return;
}
其它操作:
如求取前驱,后继等操作,类似于Treap
void insert(int &k,int val,int pos){ //插入操作if(!k){k=++sz;T[k].ct=T[k].siz=1;T[k].fa=pos;T[k].son[0]=T[k].son[1]=0;T[k].val=val;dist=k;return; }if(val==T[k].val){dist=k;T[k].siz++;T[k].ct++;return;}if(val<T[k].val) insert(T[k].son[0],val,k);if(val>T[k].val) insert(T[k].son[1],val,k);up(k);
}
int searchRANK(int k,int x){ //查询x排在第几if(!k) return 0;if(x<T[k].val) return searchRANK(L,x);if(x==T[k].val) return T[L].siz+1; if(x>T[k].val) return T[L].siz+T[k].ct+searchRANK(R,x);
}
int searchPLACE(int k,int x){ //查询排在x的数是几if(!k) return 0;if(x<=T[L].siz) return searchPLACE(L,x);x-=T[L].siz;if(x<=T[k].ct) return T[k].val;x-=T[k].ct;return searchPLACE(R,x);
}
void pre(int k,int val){ //前驱,dist记录位置if(!k) return;if(val<=T[k].val) pre(L,val);else dist=k,pre(R,val);
}
void ahe(int k,int val){ //后继if(!k) return;if(val>=T[k].val) ahe(R,val);else dist=k,ahe(L,val);
}
合并:
①当S1中的所有元素小于S2(比如S1和S2是刚刚分裂出来的)时,只需要把S1最大的点伸展到根,然后连边即可。
②当S1和S2大小任意时,启发式合并,把小的往大的身上挪。
分裂:(以k为界限,左边小于或等于k,右边大于或等于k)
BZOJ3224模板:
#include<bits/stdc++.h>
#define L T[k].son[0]
#define R T[k].son[1]
#define MAXN 100005
using namespace std;
int read(){char c;int x=0,y=1;while(c=getchar(),(c<'0'||c>'9')&&c!='-');if(c=='-') y=-1;else x=c-'0';while(c=getchar(),c>='0'&&c<='9') x=x*10+c-'0';return x*y;
}
int root,dist,sz,n;
struct node{int fa,siz,ct,val,son[2];
}T[MAXN];
void clear(int k){T[k].siz=T[k].ct=T[k].fa=T[k].val=T[k].son[0]=T[k].son[1]=0;
}
void up(int k){T[k].siz=T[L].siz+T[R].siz+T[k].ct;
}
int get(int k){return T[T[k].fa].son[1]==k;
}
void rotate(int &k){int fa=T[k].fa,gran=T[fa].fa;int d1=get(k),d2=get(fa);T[T[k].son[d1^1]].fa=fa;T[fa].son[d1]=T[k].son[d1^1];T[k].son[d1^1]=fa;T[k].fa=gran;T[fa].fa=k;if(gran) T[gran].son[d2]=k;;up(fa);up(k);
}
void splay(int k){for(int fa;fa=T[k].fa;rotate(k))if(T[fa].fa) rotate(get(fa)==get(k)?fa:k);root=k;
}
void insert(int &k,int val,int pos){if(!k){k=++sz;T[k].ct=T[k].siz=1;T[k].fa=pos;T[k].son[0]=T[k].son[1]=0;T[k].val=val;dist=k;return; }if(val==T[k].val){dist=k;T[k].siz++;T[k].ct++;return;}if(val<T[k].val) insert(T[k].son[0],val,k);if(val>T[k].val) insert(T[k].son[1],val,k);up(k);
}
int searchRANK(int k,int x){if(!k) return 0;if(x<T[k].val) return searchRANK(L,x);if(x==T[k].val) return T[L].siz+1; if(x>T[k].val) return T[L].siz+T[k].ct+searchRANK(R,x);
}
int searchPLACE(int k,int x){if(!k) return 0;if(x<=T[L].siz) return searchPLACE(L,x);x-=T[L].siz;if(x<=T[k].ct) return T[k].val;x-=T[k].ct;return searchPLACE(R,x);
}
void pre(int k,int val){if(!k) return;if(val<=T[k].val) pre(L,val);else dist=k,pre(R,val);
}
void ahe(int k,int val){if(!k) return;if(val>=T[k].val) ahe(R,val);else dist=k,ahe(L,val);
}
int find(int k,int val){if(!k) return 0;if(val==T[k].val){splay(k);return k;}return find(T[k].son[val>T[k].val],val);
}
void delet(int x){int pl=find(root,x);if(!pl) return;if(T[root].ct>1){T[root].ct--,T[root].siz--;return;}if(!T[root].son[1]&&!T[root].son[0]){clear(root),root=0;return;}if(!T[root].son[1]||!T[root].son[0]){int rt=root;root=T[root].son[0]+T[root].son[1];T[root].fa=0;clear(rt);return;}int rt=root;pre(root,x);splay(dist);T[T[rt].son[1]].fa=root;T[root].son[1]=T[rt].son[1];clear(rt);up(root);T[root].fa=0;return;
}
int main()
{n=read();for(int i=1;i<=n;i++){int x=read(),y=read();if(x==1) insert(root,y,0),splay(dist);if(x==2) delet(y);if(x==3) printf("%d\n",searchRANK(root,y));if(x==4) printf("%d\n",searchPLACE(root,y));if(x==5) dist=0,pre(root,y),printf("%d\n",T[dist].val);if(x==6) dist=0,ahe(root,y),printf("%d\n",T[dist].val); }return 0;
}
文献资料:图片转自博客ZigZagK,感谢ZZK大佬
这篇关于平衡树学习(2)——Splay的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!