面试150 颠倒二进制位 位运算分治 逻辑右移

本文主要是介绍面试150 颠倒二进制位 位运算分治 逻辑右移，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

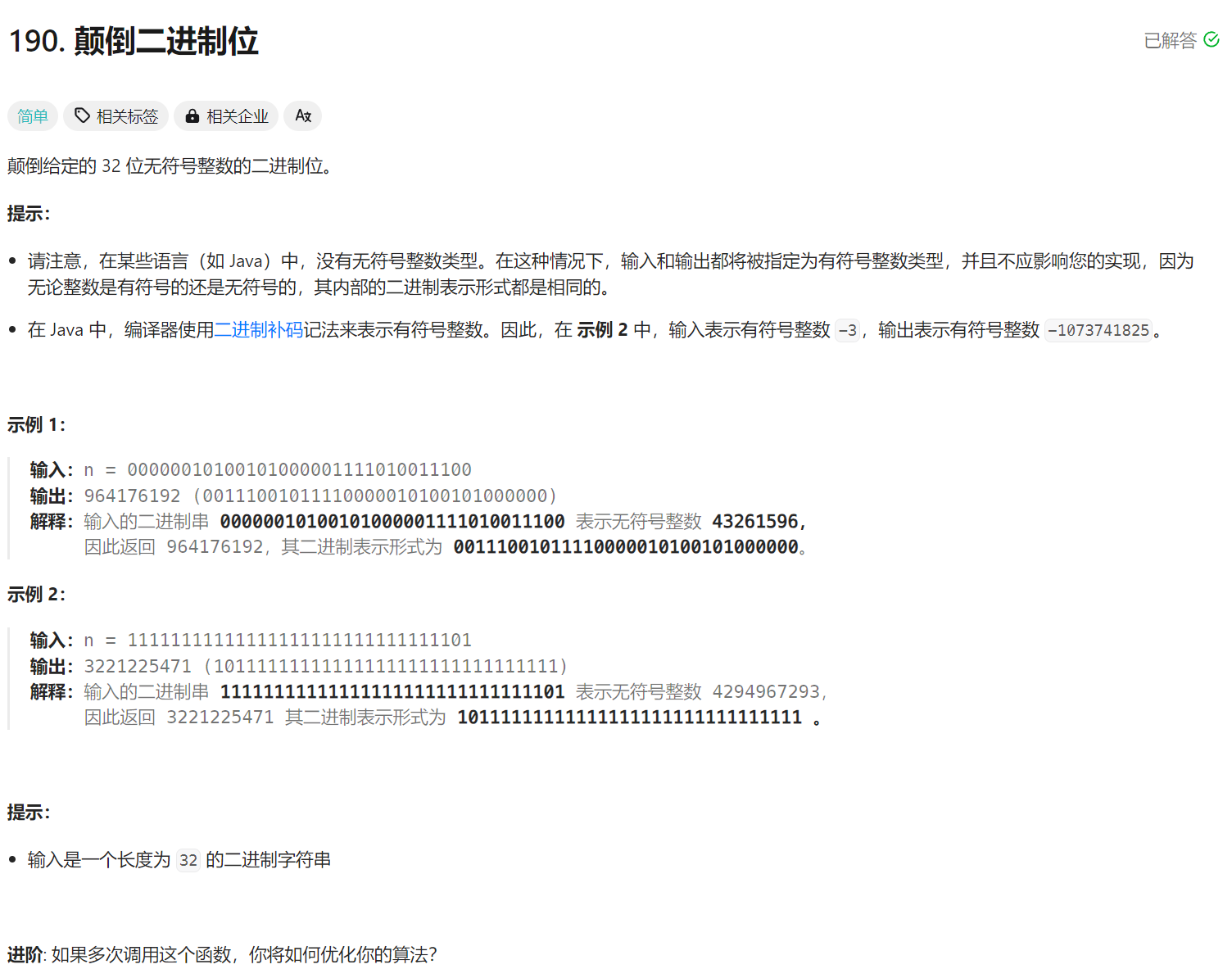
Problem: 190. 颠倒二进制位

思路

👨‍🏫 参考题解
>>>：逻辑右移（符号位一起移动，高位补零）

复杂度

时间复杂度: $O(\log n)$

空间复杂度: $O(1)$

位运算分治法

public class Solution {
//	private static final int M1 = 0x55555555; // 01010101010101010101010101010101private static final int M1 = 0B01010101010101010101010101010101; // 01010101010101010101010101010101private static final int M2 = 0x33333333; // 00110011001100110011001100110011private static final int M4 = 0x0f0f0f0f; // 00001111000011110000111100001111private static final int M8 = 0x00ff00ff; // 00000000111111110000000011111111public int reverseBits(int n){
//    	>>> 逻辑右移（符号位一起移动）n = n >>> 1 & M1 | (n & M1) << 1;// 交换相邻 1 个n = n >>> 2 & M2 | (n & M2) << 2;// 交换相邻 2 个n = n >>> 4 & M4 | (n & M4) << 4;// 交换相邻 4 个n = n >>> 8 & M8 | (n & M8) << 8;// 交换相邻 8 个return n >>> 16 | n << 16;// 交换相邻的 16 个}
}

这篇关于面试150 颠倒二进制位 位运算分治 逻辑右移的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---