本文主要是介绍【论文解读 IJCAI 2019 | PP-GCN】Fine-grained Event Categorization with Heterogeneous GCN,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

论文链接:https://arxiv.org/abs/1906.04580
代码链接:https://github.com/RingBDStack/PPGCN
来源:IJCAI 2019
关键词:HIN,细粒度事件分类,hyper-edge,GCN
文章目录
- 1 摘要
- 2 介绍
- 2.1 社交事件(social event)
- 2.2 挑战
- 2.3 已有的工作
- 2.4 作者提出
- 2.5 贡献
- 3 异质事件建模(Heterogeneous Event Modeling)
- 3.1 HIN中的事件建模
- 3.2 定义
- 4 提出的模型
- 4.1 事件相似度度量
- 4.2 Pairwise Popularity GCN Model(PP-GCN)
- 5 实验
- 6 总结
1 摘要
本文设计了一个事件元模式(event meta-schema)来描述社交事件间的语义关联,并构建了一个基于事件的HIN,用于从外部知识库整合信息。
基于细粒度的社交事件分类模型,本文提出了PP-GCN(Pairwise Popularity Graph Convolutional Network)模型。
本文提出了 基于知识元路径实例的社交事件相似度度量(KIES),并且构建了带权重的邻接矩阵作为PP-GCN模型的输入。
在真实数据集上进行了社交事件检测和聚类的任务,证明了模型的有效性。
2 介绍
2.1 社交事件(social event)
每时每刻都有很多事件在发生,比如集会、名人活动、体育赛事等等。社会媒体已成为宣传这些活动的主要媒介。
社会媒体上发布的事件通常会吸引许多评论和转发,这些评论或转发通常都带有评论者/转发者的观点和情绪,这些内容可以反映出公众对社会、政治、经济等问题的观点和态度。
对社交媒体上的帖子进行挖掘,比如进行细粒度的社交事件分类,有着广泛的应用场景。比如信息整理、预测分析、灾害风险分析等等。
总之,细粒度的社交事件分类主要关注于事件检测和事件聚合。
2.2 挑战
细粒度的社交事件分类和传统的文本挖掘/社交网络挖掘相比,面临着更多的挑战。因为社交事件是社交网络和其上的信息流的结合。
(1)一方面,建模社交事件是非常复杂和模糊的。
描述社会事件的文本通常是短文本,而且包含许多类型的实体(比如 人, 位置, 数量, 组织, 时间等)。
而且,社交网络中的用户可以对事件进行评论或者转发。因此,建模社会事件需要考虑异质的元素,以及社交网络中的帖子间显式和隐式的网络结构。
(2)另一方面,细粒度的时间分类模型通常在类别数很大但每个类别的样本数很少的情况下,有着性能瓶颈。
2.3 已有的工作
有一些研究是使用同质图或者人为设计框架,以用于社交事件的建模和抽取。
一些研究者将社交事件看成同质的words/elements共现的图,将不同尺度的异常连接的连通子图视为社会事件。
尽管这些研究在一些领域取得了很好的效果,但是在开放域的事件检测和聚类应用中的分类准确率并不理想。
另一种思路是,使用手动定义的基于框架的事件的定义,应用定义好的技术从新闻中提取社会事件框架。
这种基于框架的事件抽取可以抽取出实体和关系,但是局限于很有限的事件类型,例如:地震、股市、场馆、政治。而且,这种方法通常使用多个复杂的机器学习模型,以学习到不同层次的特征,不是端到端的学习。
社交媒体事件可以视为多个事件元素(event elements)的共现,包括主题、日期、地点、任务、组织、关键词等。
模拟社交媒体事件最简单的方式就是将事件看成是词袋(bag of words)。若对词语进行标注,将其标注为不同类型的实体,就可以引入更多有意义的语义信息。而且有了实体后,就可以使用外接的知识库来补充实体之间的关系信息。
2.4 作者提出
作者首先提出将短文本消息中的事件实例看做HIN中的超边(hyper-edge),和事件相关的所有关键词、实体、主题和用户都通过这条hyper-edge相连接。
作者还定义了一个元事件模式(event meta-schema)来描述社交事件间的语义关联,并且构建了基于事件的HIN。
为了丰富HIN,作者还从外部的知识库抽取了信息,作为对关系信息的补充。
作者还定义了一个基于知识元路径实例的事件相似度度量,称为KIES。
为了准确衡量元路径间的权重并且实现细粒度的事件检测,作者设计了PP-GCN模型(Pairwise Popularity Graph Convolutional Network model),以学习得到每个事件的表示。
最后,在基于HIN的事件建模中,作者使用KIES度量进行了细粒度事件聚类的实验。
2.5 贡献
和传统模型相比,本文提出的模型有以下几个优势:
(1)在HIN上进行社交事件建模,该模型可以整合事件元素,例如关键字、主题、实体、用户以及他们之间的关系。并且可以计算任意两个事件实例间的相似度。
(2)实现了state-of-the-art,并且在事件检测任务中避免了过拟合的问题。
(3)得到元路径权重 w w w的KIES可以提升细粒度事件聚类的效果。也就是说这个 w w w可以应用于其他应用中。
3 异质事件建模(Heterogeneous Event Modeling)
本节定义了在HIN中建模社交事件的问题,并介绍了一些相关概念和符号表示。
3.1 HIN中的事件建模
社交事件一般是指在社交网络上传播并且在现实世界中有一定影响力的事实,包括发布者、命名实体(如 参与者, 组织者, 地点等)、关键字、主题。将上述元素命名为面向事件的元素(event-oriented elements)。
使用现有的工具从社交文本中抽取出面向事件的元素。
https://github.com/stanfordnlp/CoreNLP
https://github.com/NLPIR-team/NLPIR
事件中这些元素之间的关系被称为事件元素关系(event-elements relationships),例如实体之间的关系、关键词之间的关系、主题之间的关系、用户之间的关系等等。需要在HIN中建立如下几种关系:
(1)建立同义主题词间的关联
作者用人工整理好的同义词(https://github.com/huyingxi/Synonyms),定义HIN中同义主题词间的关系。
(2)建立关键词和主题间的关联以及主题词间的层次关联
为了表示关键词和主题词之间的所属关系以及主题词的层次结构特征,作者使用了**层次的隐式狄利克雷分布(HLDA)**技术(https://github.com/joewandy/hlda)。
(3)建立实体间的关联
作者同时考虑了准确率和效率,建立HIN中实体间的关联,分为三步:
- 从中文的CN-DBpedia知识库中检索出同名实体作为候选实体;
- 使用词向量衡量社交事件中的实体和候选实体的相似度,从候选实体中选出相似度最高的;
- 将知识库中对齐实体之间的关系作为事件中实体间的关系。
(4)建立关键词和实体间的关联
在知识库中抽取出每个实体相关描述中的关键词,使用这个所属关系作为实体和关键词间的关联。
(5)建立用户间的关联
每个用户都有多个朋友,提前建立好他们之间的关联。
抽取出元素和关系后就可以构建一个基于事件的HIN,如图1(a)所示。社会事件可以看成是event-oriented elements的共现以及event-elements关系。因此一个事件实例可以看成是HIN中的一个子图。

3.2 定义
HIN G G G 和元路径 P P P 的定义不再赘述。
HIN G = ( V , E ) G=(V,E) G=(V,E),实体映射 ϕ : V → A \phi: V\rightarrow A ϕ:V→A,关系类型映射 ψ : E → R \psi: E\rightarrow R ψ:E→R。 G G G的元模式(meta-schema)定义为 T G = ( A , R ) T_G=(A,R) TG=(A,R),表示图中节点的实体类型都来源于 A A A,边的关系类型都来源于 R R R。
图1(b)就是基于事件的HIN的meta-schema。
4 提出的模型
本节介绍基于事件相似度度量的知识元路径实例,并且介绍PP-GCN的技术细节。
4.1 事件相似度度量
【Coup的定义】
给定一个元路径 P = ( A 1 − A 2 . . . A L + 1 ) P=(A_1-A_2...A_{L+1}) P=(A1−A2...AL+1),CouP定义为: C o u P p ( v i , v j ) = M p ( v i , v j ) CouP_p(v_i,v_j)=M_p(v_i,v_j) CouPp(vi,vj)=Mp(vi,vj)
其中, M P = W A 1 A 2 ⋅ W A 2 A 3 ⋅ ⋅ ⋅ W A L A L + 1 M_P=W_{A_1A_2}\cdot W_{A_2A_3}\cdot \cdot \cdot W_{A_LA_{L+1}} MP=WA1A2⋅WA2A3⋅⋅⋅WALAL+1, W A k A k + 1 W_{A_kA_{k+1}} WAkAk+1是类型为 A k , A k + 1 A_k, A_{k+1} Ak,Ak+1的节点在元路径 P P P模式下的邻接矩阵。
基于面向事件的元素以及事件元素间的关系,有相同event element的共现关系可以描述为“事件实例 - 元素 - 事件实例(IEI)”的形式。
基于上述的元路径,给出公式,衡量相似度: M I E I = W I E W E I T M_{IEI}=W_{IE}W^T_{EI} MIEI=WIEWEIT,也就是两个事件表示的点积,其中 W E I W_{EI} WEI是事件实例 - 元素的共现矩阵。
这个基于元路径实例的相似性度量是有效的,因为它考虑了不同的元素和不同的长度。meta-schema枚举出越多的元路径,这个相似性度量的准确率就更高。
列举一些不同长度的元路径:
- P 1 : E v e n t − ( p r o s t e d b y ) − S o c i a l u s e r − ( p o s t ) − E v e n t P_1: Event-(prosted by)-Social user-(post)-Event P1:Event−(prostedby)−Socialuser−(post)−Event
- P 2 : E v e n t − ( h a v i n g ) − W a s h i n g t o n D C − ( c a p t i a l o f ) − U n i t e d S t a t e s − ( c o n t a i n e d b y ) − E v e n t P_2: Event-(having)-Washington DC-(captial of)-United States-(contained by)-Event P2:Event−(having)−WashingtonDC−(captialof)−UnitedStates−(containedby)−Event
- P 3 : E v e n t − ( b e l o n g t o ) − P o l i t i c i a n − ( r e l e v a n t ) − p r e s i d e n t ( m e m b e r o f ) − R u l i n g P a r t y − ( c o n t a i n e d b y ) − E v e n t P_3: Event-(belong to)-Politician-(relevant)-president(member of)-Ruling Party-(contained by)-Event P3:Event−(belongto)−Politician−(relevant)−president(memberof)−RulingParty−(containedby)−Event
P 1 P_1 P1表示若两个事件实例被同一个用户发布,则它们就是相似的。 P 2 P_2 P2表示若两个事件同时提及了Washington DC和United States,则它们是相似的。 P 3 P_3 P3表示若两个事件可以通过3个元素组成的链相连,则它们是相似的。
注意,元路径不一定是对称的。
作者在基于事件的HIN上枚举了22个对称的元路径。
【KIES的定义】
为了方便比较基于不同元路径的相似度,需要将不同元路径的计数归一化。所以作者定义了基于社交事件相似度度量的知识元路径实例,称为KIES。若两个事件实例通过更重要(权重大)的元路径连接,它们之间应该越相似。
给定一组元路径 P = { P m } m = 1 M ′ P={\{P_m\}^{M^{'}}_{m=1}} P={Pm}m=1M′,事件实例 e i , e j e_i, e_j ei,ej间的KIES表示为:
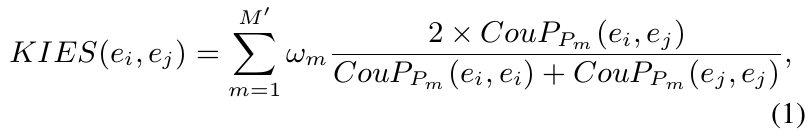
其中, C o u P P m ( e i , e j ) CouP_{P_m}(e_i,e_j) CouPPm(ei,ej)是事件实例 e i , e j e_i, e_j ei,ej间的元路径 P m P_m Pm的计数。使用参数向量 w = [ w 1 , w 2 , . . . , 2 M ′ ] w=[w_1,w_2,...,2_{M^{'}}] w=[w1,w2,...,2M′]定义元路径的权重,其中 w m w_m wm表示元路径 P m P_m Pm的权重。
K I E S ( e i , e j ) KIES(e_i,e_j) KIES(ei,ej)的定义考虑了两个方面:
- 语义上的交集,通过 e i , e j e_i, e_j ei,ej间的元路径数定义;
- 语义范围,表现为分母,由起始点和终止点都为 e i , e j e_i, e_j ei,ej自身的元路径总数定义。
因此,对于任意两个事件,均可计算出它们之间带权重的KIES距离。
4.2 Pairwise Popularity GCN Model(PP-GCN)
本节介绍如何使用PP-GCN模型实现社交媒体短文本中的细粒度事件检测。为了解决类别多但每个类别的样本数少的问题,模型还为元路径学习到了不同的权重 w w w。
PP-GCN整体架构如下图2所示:

使用KIES计算任意两个事件间的距离后,我们可以构建一个 N × N N\times N N×N的权重邻接矩阵 A A A。其中 N N N是事件数目, A i j = A j i = K I E S ( e i , e j ) A_{ij}=A_{ji}=KIES(e_i,e_j) Aij=Aji=KIES(ei,ej)。
然后使用Doc2vec为事件实例生成 d d d维的特征表示,就有了 N × d N\times d N×d维的特征矩阵 X X X。
接着使用Kipf等人提出的多层的GCN,将 A , X A, X A,X作为输入,学习有判别能力的事件表示。多层之间的信息传播定义如下:
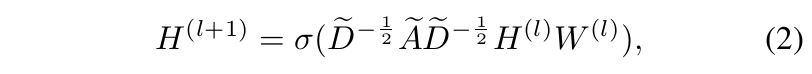
其中, A ~ = A + I N \tilde{A}=A+I_N A~=A+IN, D ~ \tilde{D} D~是对角阵, D ~ i i = ∑ j A ~ i j \tilde{D}_{ii}=\sum_j \tilde{A}_{ij} D~ii=∑jA~ij, I N I_N IN是单位矩阵, W W W是参数矩阵, l l l是层数。 σ \sigma σ为激活函数,例如Sigmoid或ReLU。
令 Z ∈ R N × F Z\in R^{N\times F} Z∈RN×F为输出的特征矩阵, F F F是每个事件表示的维度。
GCN的输入为: H ( 0 ) = X , X ∈ R N × d H^{(0)}=X, X\in R^{N\times d} H(0)=X,X∈RN×d,是事件实例的原始特征(doc2vec生成的)。输出为: H ( l ) = Z H^{(l)}=Z H(l)=Z。
但是,现实世界的社交事件通常有稀疏性的问题:类别数目很大,但是每类的事件实例数较少。
因此,作者对事件实例对进行采样,然后判断它们是否属于一个事件类别,从而训练成对(pairwise)的GCN模型。
接下来解释如何实现成对的采样(pairwise sampling)来生成训练数据:
若事件实例 e i , e j e_i, e_j ei,ej属于同一个事件类别,则将事件对 ( e i , e j ) (e_i, e_j) (ei,ej)看成是正样本对(positive-pair sample)。若事件实例 e i , e j e_i, e_j ei,ej属于不同的事件类别,则将事件对 ( e i , e j ) (e_i, e_j) (ei,ej)看成是负样本对(negative-pair sample)。
如图2所示,红色的两条线表示正样本对,灰色和蓝色的线代表负样本对。
了解了采样方法后,接着举个例子来说明样本是如何输入模型的:
(1)首先随机选择 R R R个(i.e, 1000)事件实例,然后为每个事件实例都随机选择一个正样本一个负样本,这样就生成了 R R R个正样本对和 R R R个负样本对。
(2)接着从这 2 R 2R 2R个样本对中随机选择 B B B个(i.e, 64)样本,形成一个batch,输入到模型中用于前向传播。
(3)然后重复 E E E次(e.g, 32)第(2)步,形成一个epoch。对于下一次epoch,重复上述三步。
但是,模型还有训练过程中的过拟合问题。
假定每个事件类别平均有 r r r个事件实例,每个事件实例被选为正样本对的概率为 1 r \frac{1}{r} r1,被选为负样本对的概率为 1 N − r \frac{1}{N-r} N−r1。通常 1 r ≫ 1 N − r \frac{1}{r}\gg \frac{1}{N-r} r1≫N−r1。这就可以看出,负样本对的多样性大于正样本对。
有研究学者表示,一个样本的连接概率决定了它受欢迎的程度。受这种思想的启发,作者假定在特征表示学习中,若节点受欢迎的程度越大,则其特征向量的模越大。因此,组成正样本对的两个事件实例所对应向量的模应该更接近。
因此,我们使用 Z Z Z中的特征向量的受欢迎程度来判断不同的类别。
如图2所示,对于任意两个满足 ∣ V e i ∣ ≥ ∣ V e j ∣ |V_{e_i}|\ge |V_{e_j}| ∣Vei∣≥∣Vej∣的事件实例向量 V e i , V e j V_{e_i}, V_{e_j} Vei,Vej,使用模的比值 x = ∣ V e i ∣ ∣ V e j ∣ x=\frac{|V_{e_i}|}{|V_{e_j}|} x=∣Vej∣∣Vei∣作为非线性映射函数 f ( x ) = − l o g ( x − 1 + c ) f(x)=-log(x-1+c) f(x)=−log(x−1+c)的输入,其中 c = 0.01 c=0.01 c=0.01。
我们假定正样本对的模的比值在 [ 1 , 2 ) [1,2) [1,2)范围内,所以 f ( x ) f(x) f(x)可将比值 x x x从 [ 1 , 2 ) [1,2) [1,2)映射到 ( 0 , 2 ] (0,2] (0,2],从 [ 2 , + ∞ ) [2,+\infty) [2,+∞)映射到 ( − ∞ , 0 ] (-\infty, 0] (−∞,0]。
接着使用Sigmoid函数上述的输出值映射成 0 0 0或 1 1 1,阈值为 0.5 0.5 0.5。
使用交叉熵作为损失函数,SGD迭代更新参数。
测试过程举例:测试集大小为 N N N,对于其中的任何一个事件实例 t t t。首先假定一共有 C C C个事件类别。然后分别计算 t t t和其余的 N − 1 N-1 N−1个样本的对应向量的模之比。对于每个事件类别,得到 t t t最有可能属于它的概率,选取可能性最大的作为该事件的类别。若该样本和其他所有样本的模的比值均为0,说明这个样本自成一类。
由上述的分析可知,在给定event-HIN和权重 w w w的条件下,可以计算任何两个事件实例间的相似度。
因为模型计算的是不同事件实例间的相似度(距离)信息,所以也可以应用于半监督的细粒度事件聚类任务。
5 实验
数据集:

实验任务:事件检测、事件聚类
实验结果:
(1)事件检测实验结果对比

(2)事件聚类实验结果对比

6 总结
本文解决的问题是短文本的细粒度事件抽取问题,提出了PP-GCN模型。
作者构建了一个event-HIN,将构成事件的元素看成是不同类型的节点,事件本身看成连接这些元素的超边(hyper-edge),也就是关系。
事件元素抽取的过程中引入了外部知识库,增强了模型的效果。
作者还提出了一种事件实例间相似度的度量方法:KIES(knowledgeable meta-paths instances based social event similarity, 基于知识元路径实例的社交事件相似度)。使用KIES计算出事件实例间的距离,作为邻接矩阵 A A A。使用doc2vec方法为事件实例生成初始的特征表示 X X X。两者作为GCN的输入。
KIES这里的计算是基于元路径的,而且还有参数 w w w,为不同元路径分配不同的权重。这个参数分配的可解释性有待研究。
在训练数据的获取方面,为了解决数据稀疏的问题(类别多但每个类别的样本数少),作者提出了pairwise的采样方法,为每个样本采样等数量的正样本和负样本,构成等数量的正样本对和负样本对。
为了避免训练过程中的过拟合,作者提出基于事件实例向量(GCN输出的 V V V)的模的比值做分类(这里引入popularity的概念, 受欢迎程度和模值成正比)。实验结果显示这种方法比基于向量夹角的分类器效果要好,后者随着训练迭代次数的增加,准确率增加到一定程度会显著下降,有过拟合的表现。
我觉着在过拟合的研究这方面,只是实验证明了这种方法好,有效果,但内部机理没有详细研究。
未来研究方向:
(1)元路径参数(表示不同元路径的重要性)的可解释性;
(2)将本文的模型扩展到其他的参数学习和任务中。
这篇关于【论文解读 IJCAI 2019 | PP-GCN】Fine-grained Event Categorization with Heterogeneous GCN的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







