本文主要是介绍调整Activation Function参数对神经网络的影响,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
介绍:
数据集:
模型一(tanh) :
模型二(relu):
模型三(sigmoid) :
模型四(多层tanh):
模型五(多层relu):
介绍:
Activation Function(激活函数)是一种非线性函数,应用在神经网络的每个节点(神经元)上,用来引入非线性变换,增加神经网络的表达能力。
在神经网络中,每个节点的输入是通过加权和计算得到的,然后通过激活函数进行非线性变换,得到输出。激活函数可以将输入的范围映射到一个固定的范围内,常用的范围是[0, 1]或[-1, 1]。激活函数的引入可以使神经网络具有更强的表达能力,能够处理更复杂的输入数据。
常见的激活函数有:
- Sigmoid函数:将输入映射到[0, 1]的范围内,具有平滑的非线性特性,但存在梯度消失的问题。
- ReLU函数:将输入小于0的部分映射为0,大于0的部分保持不变,具有较好的非线性特性,但存在神经元死亡的问题。
- Tanh函数:将输入映射到[-1, 1]的范围内,具有平滑的非线性特性,但也存在梯度消失的问题。
- Leaky ReLU函数:在ReLU函数的基础上,将输入小于0的部分乘以一个小的斜率,解决了神经元死亡的问题。
选择合适的激活函数取决于具体的任务和数据特点,不同的激活函数在不同的情况下会有不同的表现。
数据集:
# scatter plot of the circles dataset with points colored by class
from sklearn.datasets import make_circles
from numpy import where
from matplotlib import pyplot
# generate circles
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# select indices of points with each class label
for i in range(2):samples_ix = where(y == i)pyplot.scatter(X[samples_ix, 0], X[samples_ix, 1], label=str(i))
pyplot.legend()
pyplot.show()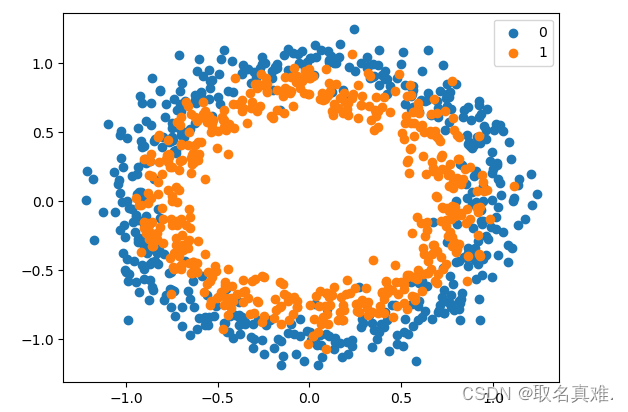
模型一(tanh) :
# mlp for the two circles classification problem
from sklearn.datasets import make_circles
from sklearn.preprocessing import MinMaxScaler
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from keras.initializers import RandomUniform
from matplotlib import pyplot
# generate 2d classification dataset
X, y = make_circles(n_samples=1000, noise=0.1, random_state=1)
# scale input data to [-1,1]
scaler = MinMaxScaler(feature_range=(-1, 1))
X = scaler.fit_transform(X)
# split into train and test
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# define model
model = Sequential()
init = RandomUniform(minval=0, maxval=1)
model.add(Dense(5, input_dim=2, activation='tanh', kernel_initializer=init))
model.add(Dense(1, activation='sigmoid', kernel_initializer=init))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot training history
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
模型二(relu):
# define model
model = Sequential()
init = RandomUniform(minval=0, maxval=1)
model.add(Dense(5, input_dim=2, activation='relu', kernel_initializer=init))
model.add(Dense(1, activation='sigmoid', kernel_initializer=init))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot training history
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
模型三(sigmoid) :
# define model
model = Sequential()
init = RandomUniform(minval=0, maxval=1)
model.add(Dense(5, input_dim=2, activation='sigmoid', kernel_initializer=init))
model.add(Dense(1, activation='sigmoid', kernel_initializer=init))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot training history
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
模型四(多层tanh):
# define model
init = RandomUniform(minval=0, maxval=1)
model = Sequential()
model.add(Dense(5, input_dim=2, activation='tanh', kernel_initializer=init))
model.add(Dense(5, activation='tanh', kernel_initializer=init))
model.add(Dense(5, activation='tanh', kernel_initializer=init))
model.add(Dense(5, activation='tanh', kernel_initializer=init))
#Initializers define the way to set the initial random weights of Keras layers. The keyword arguments used for passing
#initializers to layers depends on the layer.
model.add(Dense(5, activation='tanh', kernel_initializer=init))
model.add(Dense(1, activation='sigmoid', kernel_initializer=init))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot training history
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
模型五(多层relu):
# define model
model = Sequential()
model.add(Dense(5, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(5, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(5, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(5, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(5, activation='relu', kernel_initializer='he_uniform'))
#he_uniform . Draws samples from a uniform distribution within [-limit, limit] , where limit = sqrt(6 / fan_in)
#( fan_in is the number of input units in the weight tensor).model.add(Dense(1, activation='sigmoid'))
# compile model
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=opt, metrics=['accuracy'])
# fit model
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=500, verbose=0)
# evaluate the model
_, train_acc = model.evaluate(trainX, trainy, verbose=0)
_, test_acc = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_acc, test_acc))
# plot training history
pyplot.plot(history.history['accuracy'], label='train')
pyplot.plot(history.history['val_accuracy'], label='test')
pyplot.legend()
pyplot.show()
这篇关于调整Activation Function参数对神经网络的影响的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





