本文主要是介绍普歌-毅雁-线型表,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
线型表
- 前言
- 一、线型表是什么?
- 二、常用概念
- 结点
- 前驱
- 后继
- 第一元素,最后元素
- 三、分类
- 1.顺序表
- 创建
- 常见操作
- 特点
- 2.链表
- 定义
- 分类
- 常见操作
- 特点
- 四、两表的比较
- 跳跃表(skiplist)
- 五、线型表的特点分析
前言
在看完数据结构基础入门篇后,再来讲解一下数据结构中常用的工具线型表。

一、线型表是什么?
这里我们引入一下百度百科的概念:
将具有线性关系的数据存储到计算机中所使用的存储结构称为线型表。
因为线性表的逻辑结构简单,便于实现和操作。
二、常用概念
结点
结点又包含了两部分
数据域:存放的存储数据
指针域:存放的其它结点的地址
前驱
在逻辑上的前一个结点
后继
同理,后继就是在逻辑上的后一个结点
第一元素,最后元素
最简单的概念,他就是在分配地址时的一个元素。同理如果在创建时是静态创建时最后一个元素。
三、分类
我们都知道,在逻辑上相邻的数据在实际的物理存储中有两种形式:分散存储和集中存储,那么我们就分析一下他们各自的优缺点吧。
被划分为以下两种表:
1.顺序表
创建
在创建时会在物理地址上分配一块地方
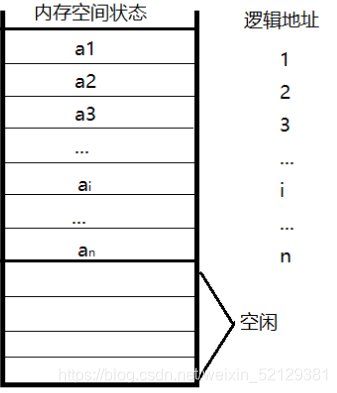
常见操作
- 顺序表的初始化
在创建后就需要对表进行初始化操作,以避免一些脏数据会影响结果
- 创建
- 查找
- 顺序表的优点就是查询速度快(随机存取特点)当按位查找时他的时间复杂度就是常量级:O(1)
- 按值查找的时间复杂度:O(n)
- 插入
时间复杂度:(On)
需要注意的是:
因为他的底层实际就是数组,如果在分配地址时分配地址有剩余,那么就会将新加入的数据添加到后面。
但是添加的数据超过最大分配地址时,就需要重新创建一个更大的表来存储。
- 删除
时间复杂度:O(n)
- 清空
- 判空
特点
- 随机访问
可以在时间复杂度为O(1)中可以找到第i个元素
- 存储密度高
在一片连续空间中就可以存储数据,因为本身就连续,不需要索引。
- 扩展不方便
因为在创建时就已经指定了大小,所以如果在扩展就需要重新分配地址。
同样的插,删数据也是相同的道理。
- 插,删数据难
2.链表
链表是一种常见的重要的数据结构。接下来让我们进一步了解他吧。
定义
什么是链表?
在这里我们引入一下百度百科的概念
链表是一种在物理结构上不连续存储结构,它是动态地进行存储分配的一种结构,由一系列结点组成。
具体的分类图解请看下文。
分类
-
单向链表
因为他是由一串结点组成的最后一个指针指向null,所以他又叫结点列表。
它又可以分为 - 带头结点 和 - 不带头结点。在不带头结点中,它的下一结点是用于存放数据的。
而头结点头指针指向的下一位是不存放数据元素的。
显然带头结点写代码更方便。
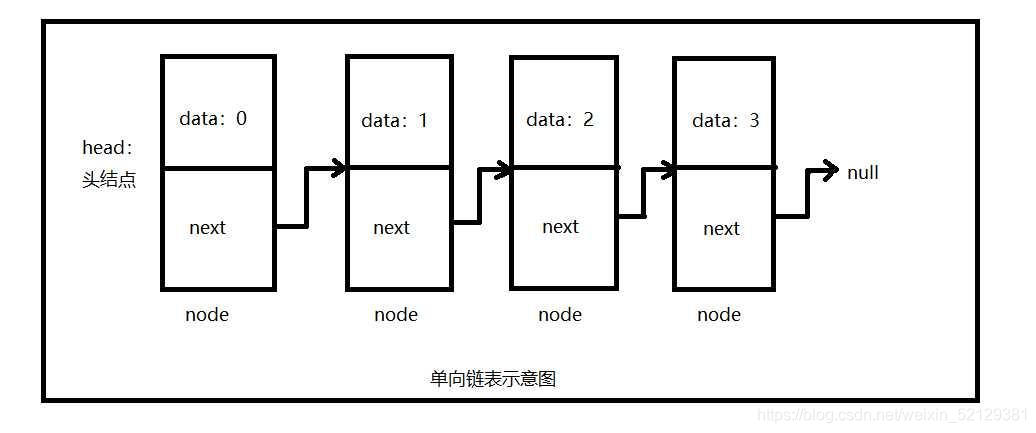
-
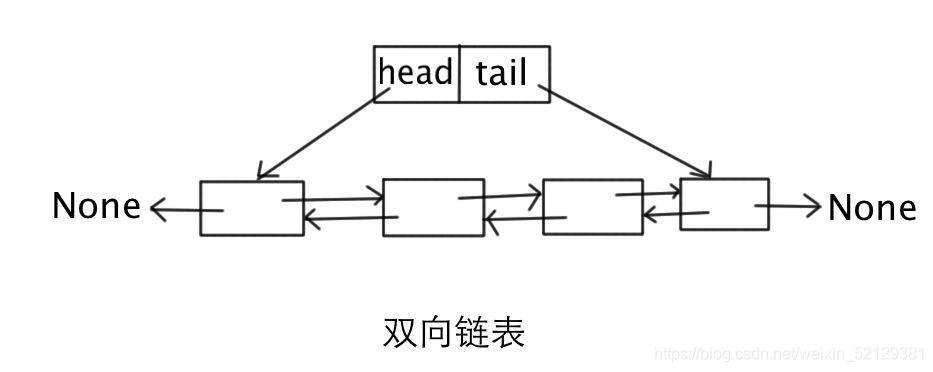
双向链表
同理双向链表就是一个节点中存储着前驱的地址和后继的地址。
-
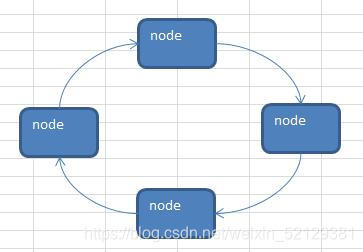
循环链表
循环链表就是头尾相连的链表
-
静态链表
静态链表就是用数组表示的链表,在物理地址上也是连续的。
常见操作
这里只针对单链表进行的操作
- 判空
- 插入
因为插入时需要对每一个结点进行判断是否是指定位置。
时间复杂度为O(n) - 前插
可以遍历一遍寻找到对应结点进行操作。
但是也可以创建一个新的链表,将插入的数据与后面的结相连,组成一个新的链表。最后将前面的链表连接上。
那么它的时间复杂度就是:O(1)
-
删除
时间复杂度为:O(n) -
查找
相比于顺序表,链表中的查找就显得比较忙了
简单理解就是你需要从头开始找到下一个引路人,告诉你下一条路这么走。
所以他的时间复杂度为:O(n) -
求长度
实际上在增,删操作时就已经引入了求长度的方法,这里就不在多赘述。
时间复杂度:O(n)
特点
- 高效的插入和删除
- 低效的随机访问
四、两表的比较
| 比较内容 | 顺序表 | 链表 |
|---|---|---|
| 存储 | 存储密度高 | 改容方便 |
| 销 | 分为自动回收和手动回收 | 每个结点依次回收 |
| 增删 | 改后面的元素都要移动 | 只需要改变指针即可 |
| 查 | 有序时可用二分查找法:O(log2n) | 按位和按值都是O(n) |
跳跃表(skiplist)
当我们遇到数据量很大时,要进行增删查操作时,在使用如上两表会很不方便,于是跳跃表就出现了
他是一种基于链表和二分查找法思想的实现
如图: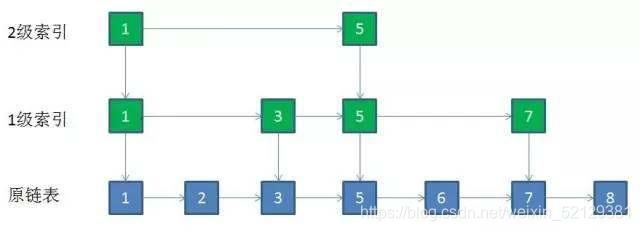
当数据过多时就可以为一些结点来添加索引
跳跃表实质上是一种空间换时间的操作。
五、线型表的特点分析
-
均匀性:
虽然数据元素可以是多种多样的,但是对于同一线型表中的各个元素他的类型和长度必须是相同的。
-
有序性:
因为他的存储是相对线型的,所以各数据元素在线性表中的位置只取决于它们的序号。
注意:其它元素前面均只有一个数据元素(直接前驱)和后面均只有一个数据元素(直接后继)
这篇关于普歌-毅雁-线型表的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!