本文主要是介绍利用matlab实现线型卡尔曼滤波(LKF),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
LKF算法模型

例题

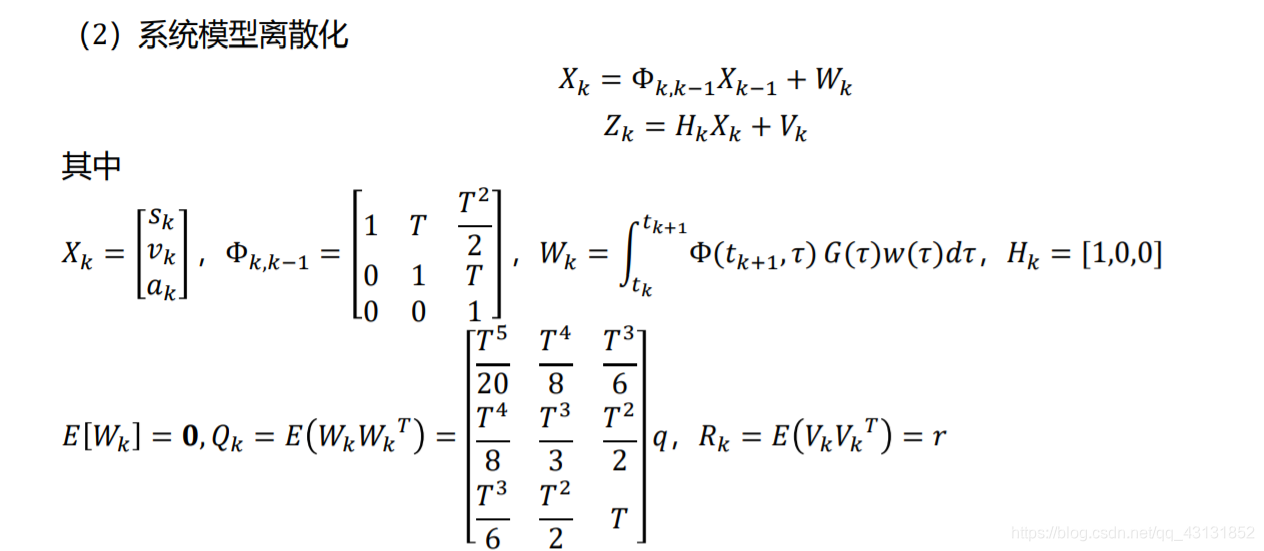
实现

观测只有位置
clc;
clear;
%测量值模拟
N=100;%观测次数
t=0:1:N-1;%假定输出周期
T=1;
x=zeros(6,N);
z=zeros(3,N);
x0=[0;0;50;0;5*cos(pi/6);5*sin(pi/6)];%真值初始值
mu1=[0;0;0;0;0;0];
mu2=[0;0;0];
Q=diag(0.1*[9,9,20.25,0.01,0.01,0.0225]);
R=diag([9,9,20.25]);rng(1);
w=mvnrnd(mu1,Q,N)';
v=mvnrnd(mu2,R,N)';
x(:,1)=x0;
for k=1:N-1x1=x(1,k);x2=x(2,k);x3=x(3,k);x4=x(4,k);x5=x(5,k);x6=x(6,k);x(:,k+1)=[x1;x2+x5*T;x3+x6*T;x4;x5;x6]+w(:,k);z(:,k+1)=x(1:3,k+1)+v(:,k+1);
end
%RLS估计
xr=zeros(6,N);
xr(:,1)=[0;0;0;0;0;0];
P=diag([1000,1000,1000,100,100,100]);
H=[eye(3),zeros(3,3)];
for k=1:N-1K=P*H'/(H*P*H'+R);xr(:,k+1)=xr(:,k)+K*(z(:,k+1)-H*xr(:,k));P=P-K*H*P;
end
%LKF估计
xk=zeros(6,N);
xk(:,1)=[0;0;0;0;0;0];
Pk=diag([1000,1000,1000,100,100,100]);
Fai=[eye(3),T.*eye(3);zeros(3,3),eye(3)];
Hk=[eye(3),zeros(3,3)];
for k=1:N-1xk(:,k)=Fai*xk(:,k);Pk=Fai*Pk*Fai'+Q;Kk=Pk*Hk'/(Hk*Pk*Hk'+R);xk(:,k+1)=xk(:,k)+Kk*(z(:,k+1)-Hk*xk(:,k));Pk=(eye(6)-Kk*Hk)*Pk*(eye(6)-Kk*Hk)'+Kk*R*Kk';
end
输出结果:
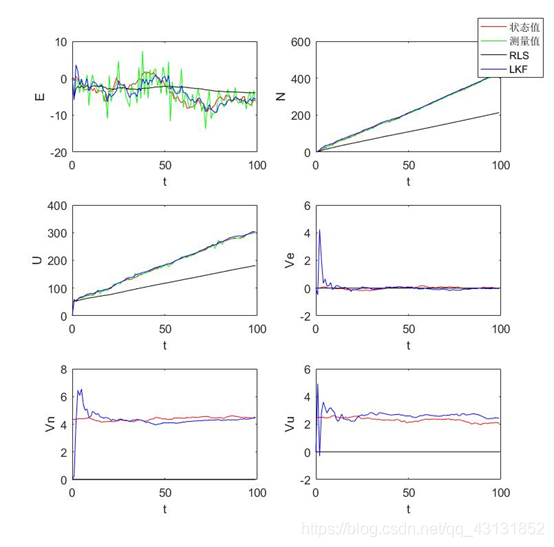
真实值、观测值、递推最小二乘估计值和卡尔曼滤波法估计值曲线如下图:
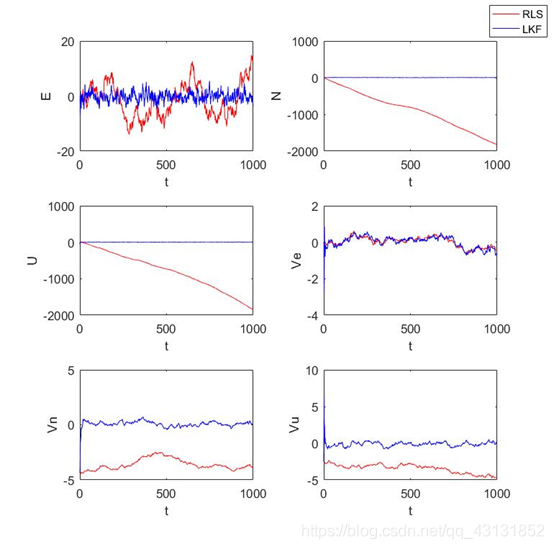
递推最小二乘估计值和卡尔曼滤波法估计值与真实值的误差如下图:
观测只有速度
clc;
clear;
%测量值模拟
N=100;%观测次数
t=0:1:N-1;%假定输出周期
T=1;
x=zeros(6,N);
z=zeros(3,N);
x0=[0;0;50;0;5*cos(pi/6);5*sin(pi/6)];%真值初始值
mu1=[0;0;0;0;0;0];
mu2=[0;0;0];
Q=diag(0.1*[9,9,20.25,0.01,0.01,0.0225]);
R=diag([0.01;0.01;0.0225]);rng(1);
w=mvnrnd(mu1,Q,N)';
v=mvnrnd(mu2,R,N)';
x(:,1)=x0;
for k=1:N-1x1=x(1,k);x2=x(2,k);x3=x(3,k);x4=x(4,k);x5=x(5,k);x6=x(6,k);x(:,k+1)=[x1;x2+x5*T;x3+x6*T;x4;x5;x6]+w(:,k);z(:,k+1)=x(4:6,k+1)+v(:,k+1);
end
%RLS估计
xr=zeros(6,N);
xr(:,1)=[0;0;0;0;0;0];
P=diag([1000,1000,1000,100,100,100]);
H=[zeros(3,3),eye(3)];
for k=1:N-1K=P*H'/(H*P*H'+R);xr(:,k+1)=xr(:,k)+K*(z(:,k+1)-H*xr(:,k));P=P-K*H*P;
end
%LKF估计
xk=zeros(6,N);
xk(:,1)=[0;0;0;0;0;0];
Pk=diag([1000,1000,1000,100,100,100]);
Fai=eye(6);
Hk=[zeros(3,3),eye(3)];
for k=1:N-1xk(:,k)=Fai*xk(:,k);Pk=Fai*Pk*Fai'+Q;Kk=Pk*Hk'/(Hk*Pk*Hk'+R);xk(:,k+1)=xk(:,k)+Kk*(z(:,k+1)-Hk*xk(:,k));Pk=(eye(6)-Kk*Hk)*Pk*(eye(6)-Kk*Hk)'+Kk*R*Kk';
end
输出结果:
真实值、观测值、递推最小二乘估计值和卡尔曼滤波法估计值曲线如下图:

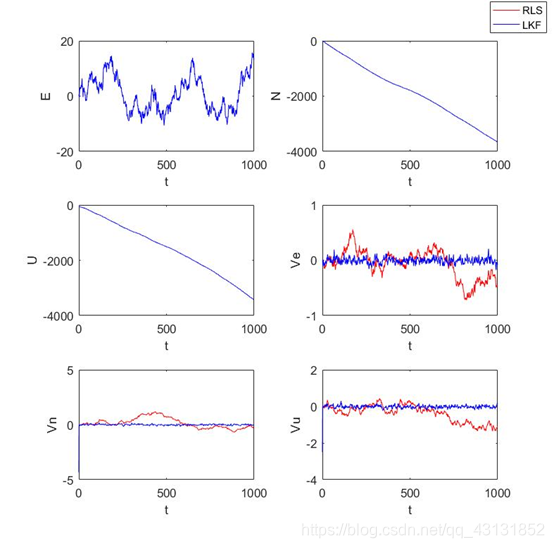
递推最小二乘估计值和卡尔曼滤波法估计值与真实值的误差如下图:
观测既有位置又有速度
clc;
clear;
%测量值模拟
N=100;%观测次数
t=0:1:N-1;%假定输出周期
T=1;
x=zeros(6,N);
z=zeros(6,N);
x0=[0;0;50;0;5*cos(pi/6);5*sin(pi/6)];%真值初始值
mu=[0;0;0;0;0;0];
Q=diag(0.1*[9,9,20.25,0.01,0.01,0.0225]);
R=diag([9,9,20.25,0.01,0.01,0.0225]);rng(1);
w=mvnrnd(mu,Q,N)';
v=mvnrnd(mu,R,N)';
x(:,1)=x0;
for k=1:N-1x1=x(1,k);x2=x(2,k);x3=x(3,k);x4=x(4,k);x5=x(5,k);x6=x(6,k);x(:,k+1)=[x1;x2+x5*T;x3+x6*T;x4;x5;x6]+w(:,k);z(:,k+1)=x(:,k+1)+v(:,k+1);
end
%RLS估计
xr=zeros(6,N);
xr(:,1)=[0;0;0;0;0;0];
P=diag([1000,1000,1000,100,100,100]);
H=eye(6);
for k=1:N-1K=P*H'/(H*P*H'+R);xr(:,k+1)=xr(:,k)+K*(z(:,k+1)-H*xr(:,k));P=P-K*H*P;
end
%LKF估计
xk=zeros(6,N);
xk(:,1)=[0;0;0;0;0;0];
Pk=diag([1000,1000,1000,100,100,100]);
Fai=[eye(3),T.*eye(3);zeros(3,3),eye(3)];
Hk=eye(6);
for k=1:N-1xk(:,k)=Fai*xk(:,k);Pk=Fai*Pk*Fai'+Q;Kk=Pk*Hk'/(Hk*Pk*Hk'+R);xk(:,k+1)=xk(:,k)+Kk*(z(:,k+1)-Hk*xk(:,k));Pk=(eye(6)-Kk*Hk)*Pk*(eye(6)-Kk*Hk)'+Kk*R*Kk';
end
输出结果:
真实值、观测值、递推最小二乘估计值和卡尔曼滤波法估计值曲线如下图:
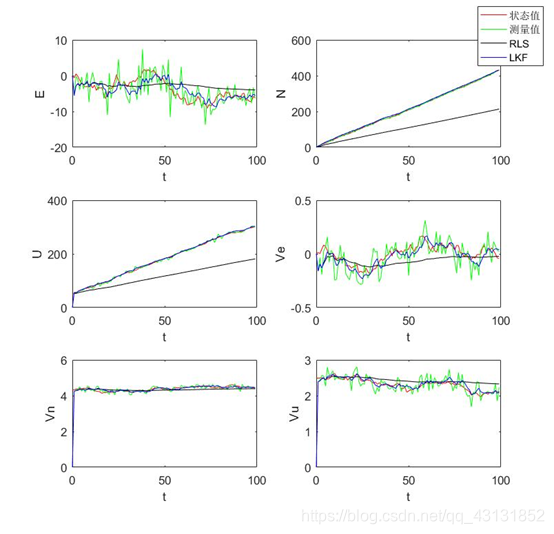
递推最小二乘估计值和卡尔曼滤波法估计值与真实值的误差如下图:
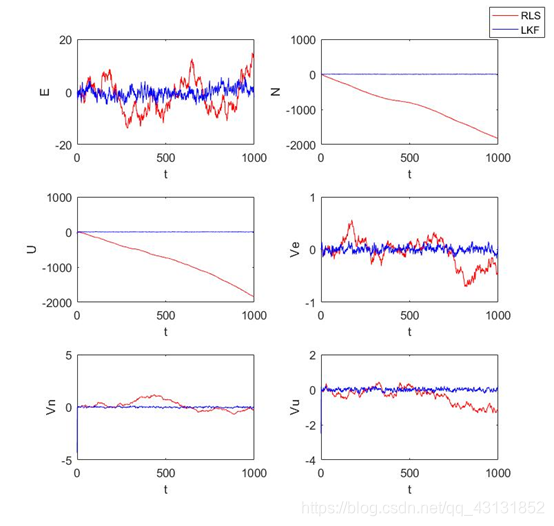
这篇关于利用matlab实现线型卡尔曼滤波(LKF)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


