本文主要是介绍从roc曲线到auc,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.为什么我们要用roc曲线进行评价
用传统的识别率来评价模型的话会有下面的缺陷:
在类不平衡的情况下,
如正样本90个,负样本10个,直接把所有样本分类为正样本,得到识别率为90%
而如果正样本识别对75个,负样本识别对5个,得到的识别率为80%。
但是这样的识别率评价指标导致高分模型不具有鲁棒性(即该模型在类别平衡下表现不好)
所以我们要换一种评价指标就有了roc曲线
2.那么roc曲线到底是什么呢?
对于一个二分类问题,我们有如下图4种情况
i. 预测为正,真实为正(预测正确)即下图的:TP
ii.预测为正,真实为反(预测错误)即下图的:FP
iii.预测为反,真实为正(预测正确)即下图的:FN
iv.预测为反,真实为反(预测错误)即下图的:TN

然后我们假定两个属性TPR和FPR,
TPR(灵敏度)=正样本预测正确结果数 / 正样本实际数
TPR=TP/(TP+FN)
FPR(特制度)=被预测为正的负样本结果数 /负样本实际数
FPR=FP/(FP+TN)
以FPR为横轴,TPR为负轴作图就有了roc曲线

我们从几个特殊点看是怎么反应指标的
第一个点,(0,1)
即FPR=0, TPR=1,这意味着FN(false negative)=0,并且FP(false positive)=0。Wow,这是一个完美的分类器,它将所有的样本都正确分类。
第二个点,(1,0)
即FPR=1,TPR=0,类似地分析可以发现这是一个最糟糕的分类器,因为它成功避开了所有的正确答案。
第三个点,(0,0)
即FPR=TPR=0,即FP(false positive)=TP(true positive)=0,可以发现该分类器预测所有的样本都为负样本(negative)。
第四个点(1,1)
分类器实际上预测所有的样本都为正样本。
综上所述
我们可以断言,ROC曲线越接近左上角,该分类器的性能越好,也就防止了类别不平衡导致的错误评分
3.那么我们怎么画roc曲线呢?
这里我借用大多数博客的内容来说
“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率

接下来,我们从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:

其中这就是roc曲线了,可以看到如果阀值越多,我们的点越多roc曲线越平滑
4.roc曲线和auc什么关系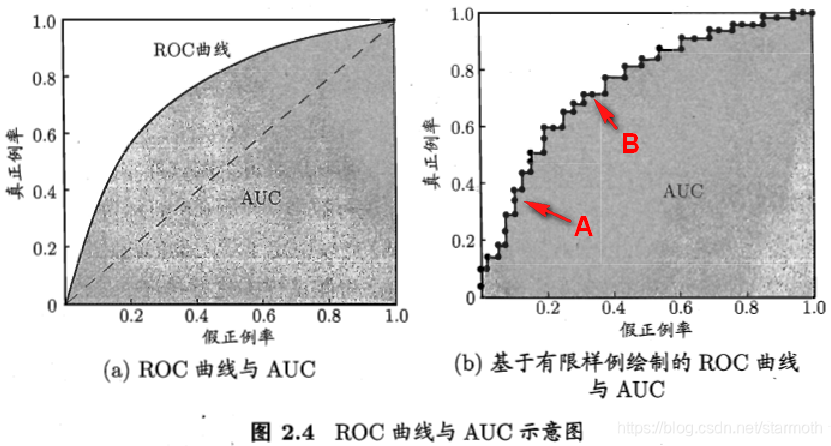
这两个图很清晰得表面了两种关系:
即auc为roc曲线以下的部分
5.auc表示了什么?
AUC(Area Under Curve)被定义为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测,因此不存在AUC < 0.5的情况。
综上auc的值往往反应了模型的分类效果好不好鲁棒性强不强。是个非常适用的指标
这篇关于从roc曲线到auc的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








