判断一个素数是否可以写成两个立方数的差（预处理+二分）

本文主要是介绍判断一个素数是否可以写成两个立方数的差（预处理+二分），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

立方差公式为：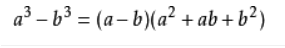
反证法：如果一个素数等于上面那个式子，在（a-b）≠1的情况下，它就有两个因子，就违背了素数的概念。这样的话，（a-b）必定为1，也就是a和b相差为1.我们预处理出题目要求范围内（x^3）-(x-1) ^3，对于给定的素数，二分去查找包不包含这个值。
代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define ll long long
using namespace std;const int maxx=1e5+100;
ll f[maxx];
int n;inline void init()
{for(ll i=1;i<=1e5;i++) f[i]=(i*i*i)-(i-1)*(i-1)*(i-1);
}
int main()
{int t;scanf("%d",&t);init();while(t--){scanf("%lld",&n);int pos=lower_bound(f+1,f+1+100000,n)-f;if(f[pos]==n) cout<<"YES"<<endl;else cout<<"NO"<<endl;}return 0;
}

努力加油a啊，(^o)/~

这篇关于判断一个素数是否可以写成两个立方数的差（预处理+二分）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---