本文主要是介绍leetcode209长度最小的子数组|滑动窗口算法详细讲解学习,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
滑动窗口是一种基于双指针的一种思想,两个指针指向的元素之间形成一个窗口。
分类:窗口有两类,一种是固定大小类的窗口,一类是大小动态变化的窗口。
简而言之,滑动窗口算法在一个特定大小的字符串或数组上进行操作,而不在整个字符串和数组上操作,这样就降低了问题的复杂度,从而也达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口主要应用在数组和字符串上。
https://leetcode.cn/problems/2VG8Kg/
给定一个含有 n 个正整数的数组和一个正整数 target**。**
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数组,返回 0 。
示例 1:
**输入:**target = 7, nums = [2,3,1,2,4,3] **输出:**2 **解释:**子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
**输入:**target = 4, nums = [1,4,4] **输出:**1
示例 3:
**输入:**target = 11, nums = [1,1,1,1,1,1,1,1] **输出:**0
暴力求解
class Solution {public:int minSubArrayLen(int target, vector<int>& nums) {int n=nums.size();int resLen=10*10*10*10*10;for(int i=0;i<n;i++){int sum=0;int len=0;for(int j=i;j<n;j++){sum+=nums[j];if(sum>=target){len=j-i+1;resLen=resLen<len?resLen:len;break;}}}return resLen==10*10*10*10*10?0:resLen;}
};
- 时间复杂度是O(n^2)
- 空间复杂度是O(1)
滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢。
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
那么问题来了, 滑动窗口的起始位置如何移动呢?
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
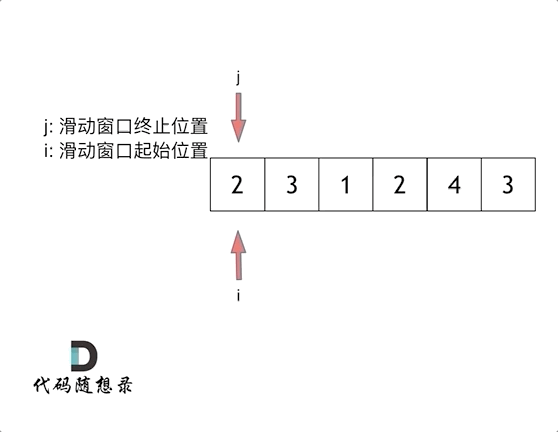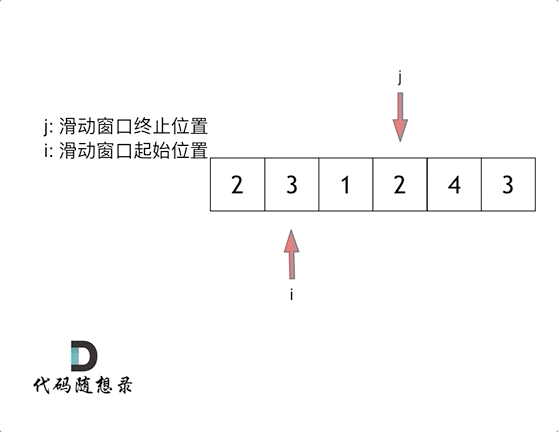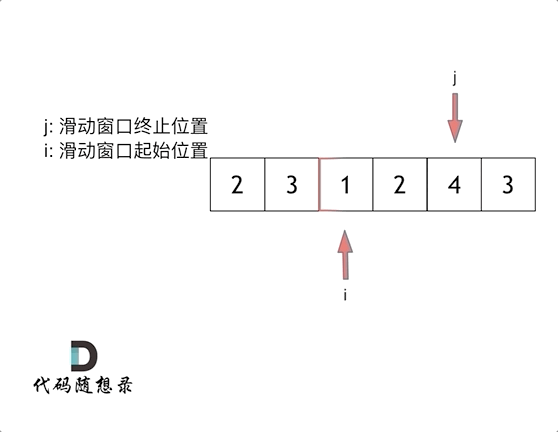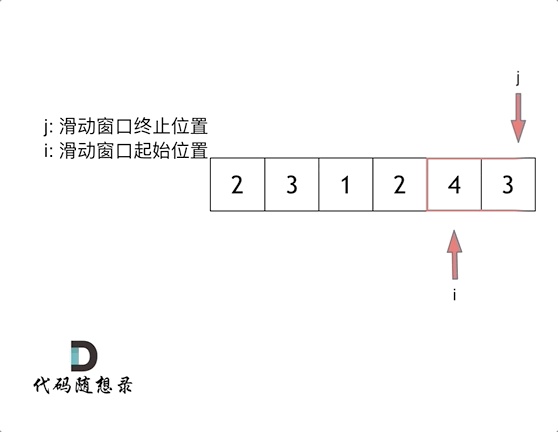
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int resLen=INT32_MAX;//resLen是结果长度int sum=0;int i=0;//滑动窗口的起始指针int j;//滑动窗口的终止指针for(j=0;j<nums.size();j++){ sum+=nums[j];while(sum>=target){int len=j-i+1;resLen=resLen<len?resLen:len;sum-=nums[i];i++;}}return resLen==INT32_MAX?0:resLen;}
};
int的取值范围依赖于计算机系统。在16位机器中,int占16位,其中一位为符号位,所以取值范围为-32768~32767。而在32位和64位机器中,int占32位或64位,取值范围分别为-2147483648~2147483647和-9223372036854775808~9223372036854775807。
int resLen=INT32_MAX; 这行代码表示定义了一个整型变量 resLen 并将其初始化为 INT32_MAX。
INT32_MAX 是 C++ 中的一个常量,表示 32 位整数的最大值。在大多数平台上,这个值是 2147483647。
所以,这行代码的目的是初始化 resLen 为一个非常大的数,这样在后续的代码中,如果 resLen 被修改为更小的值,就可以通过比较轻易地检测出来。这是一种常见的编程技巧,用于初始化变量或标志为某个非常大的值或默认值。
这篇关于leetcode209长度最小的子数组|滑动窗口算法详细讲解学习的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





