【数据结构】二叉树篇| 纲领思路01+刷题

本文主要是介绍【数据结构】二叉树篇| 纲领思路01+刷题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

博主简介：努力学习的22级计算机科学与技术本科生一枚🌸
博主主页： @是瑶瑶子啦
每日一言🌼: 所谓自由，不是随心所欲，而是自我主宰。——康德

一、二叉树刷题纲领

🍊 二叉树解题的思维模式分两类：
- 1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。(对应：回溯算法）
```
void traverse(TreeNode root) {if (root == null) {return;}// 前序位置traverse(root.left);// 中序位置traverse(root.right);// 后序位置
}
```
- 2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。（对应：动态规划算法）
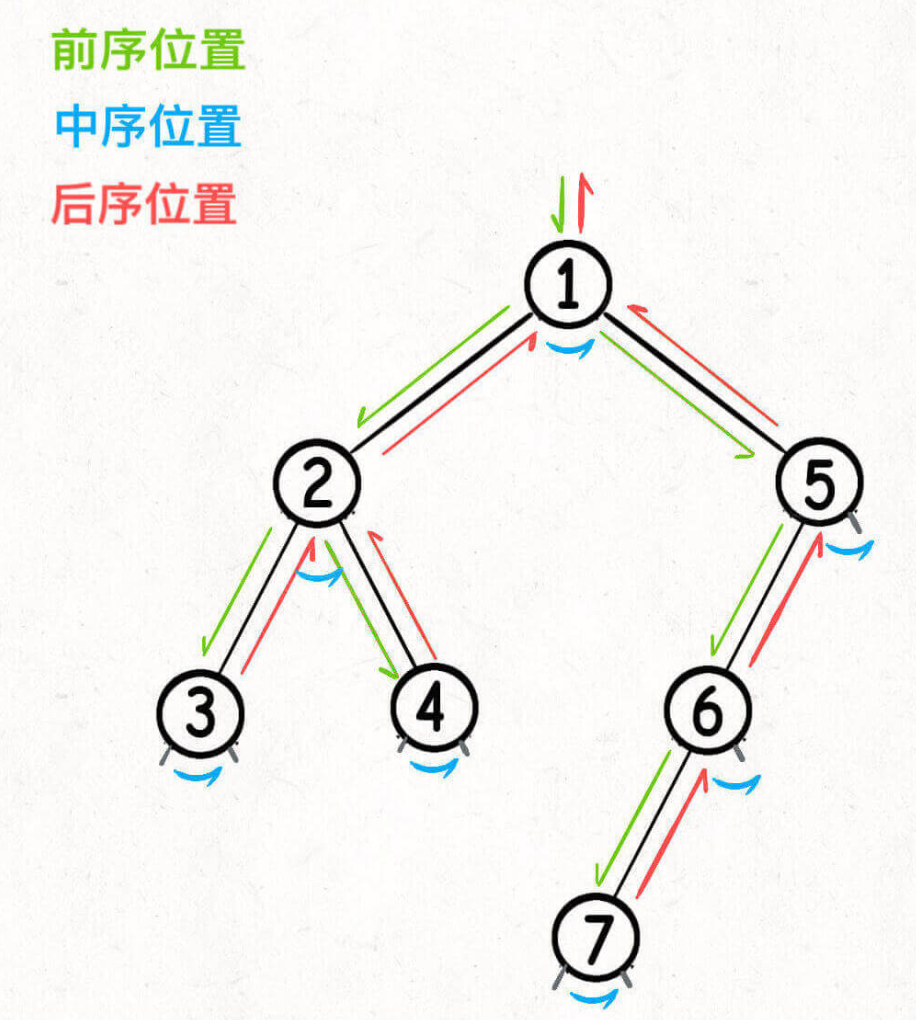
🍊 前中后序
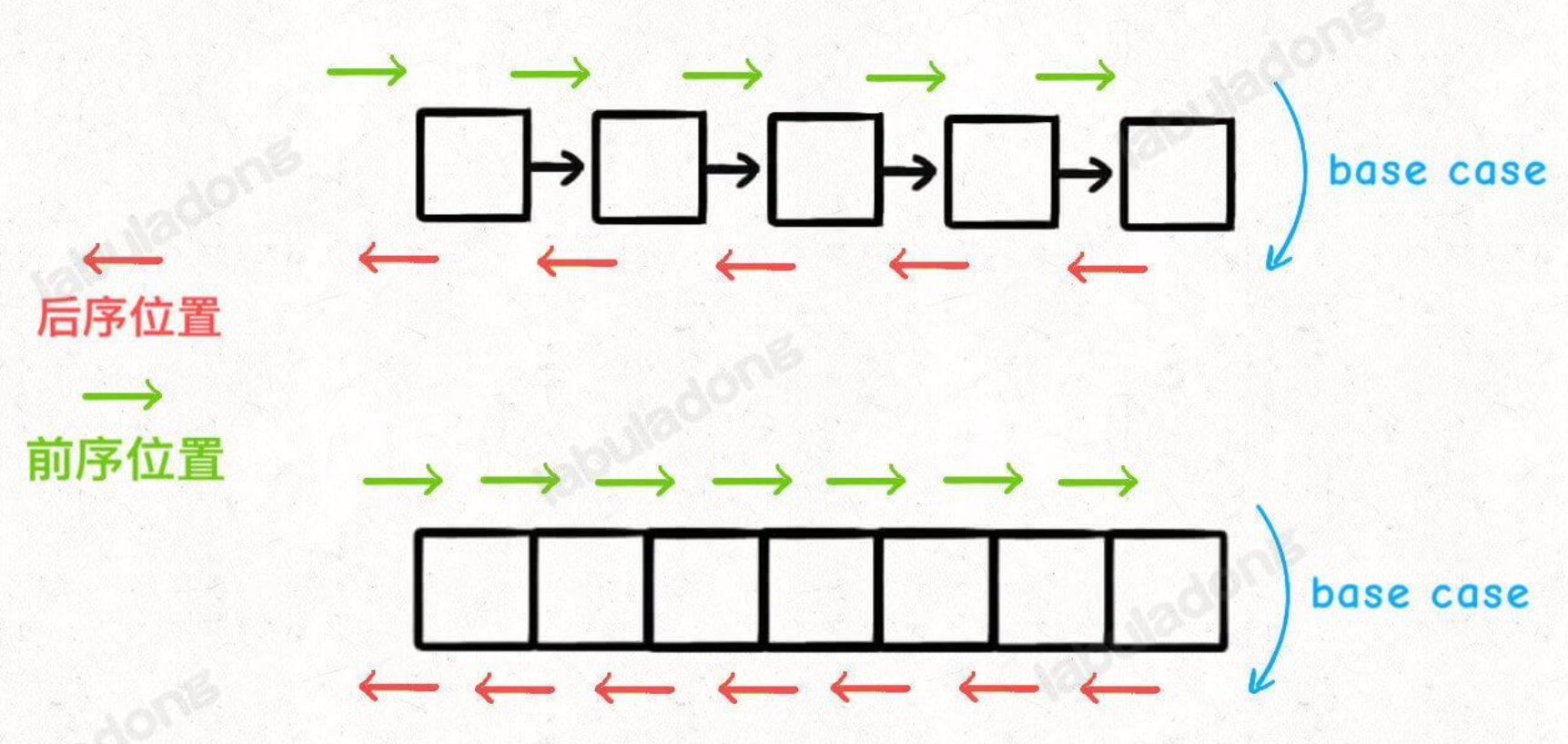
- 所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候，那么进一步，你把代码写在不同位置，代码执行的时机也不同
- 前序位置的代码只能从函数参数中获取父节点传递来的数据，而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。
- 🌟二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。
🍊一道二叉树的题目时的通用思考过程
1. 是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现。
2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。
3. 无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

二、刷题

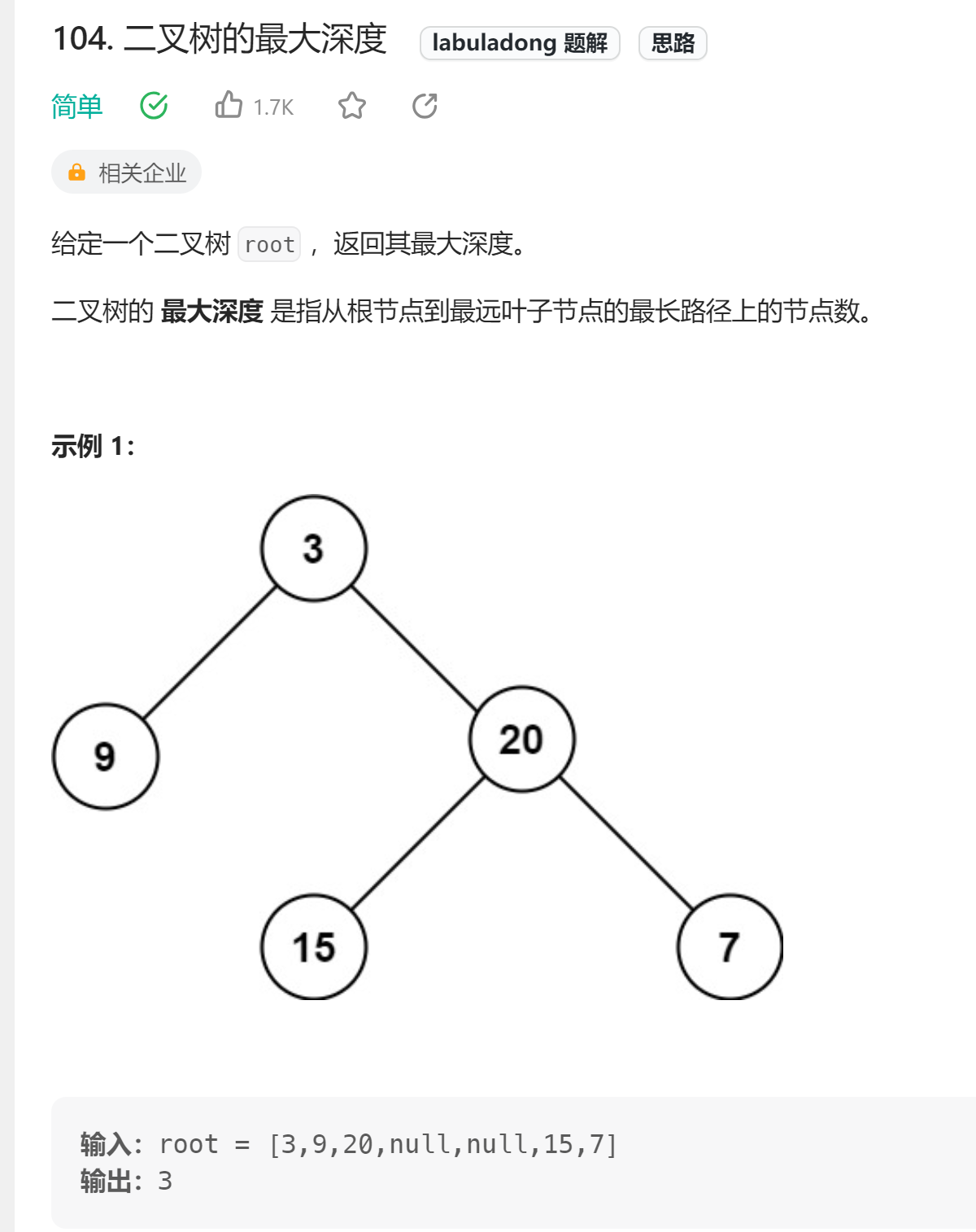
1、104. 二叉树的最大深度

🔗104. 二叉树的最大深度
在这里插入图片描述

👧🏻思路：分解成子问题，maxDepth = 1 + 左子树最大高度+右子树最大高度

🙇🏻‍♀️代码：

 public int maxDepth(TreeNode root) {//临界条件if(root == null){return 0;}int leftHeight = maxDepth(root.left);//求左子树最大高度int rightHeight = maxDepth(root.right);//求右子树最大高度return 1 + Math.max(leftHeight, rightHeight);}

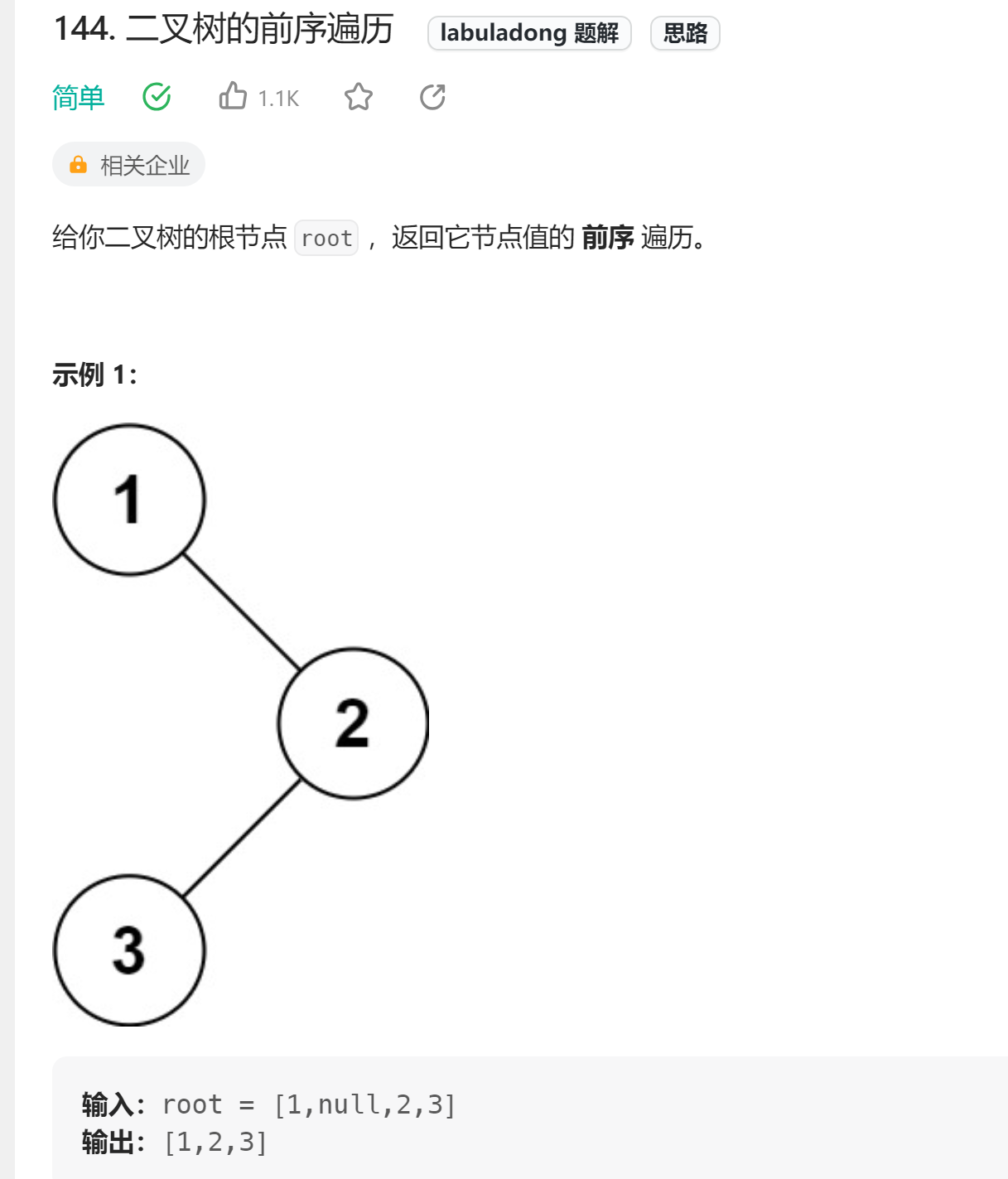
2、二叉树的前序遍历（非递归）

🔗144. 二叉树的前序遍历
在这里插入图片描述

👧🏻思路：分解成子问题，递归序列 = add(自身节点）+ add(左子树的递归序列） + add(右子树的递归序列）

🙇🏻‍♀️代码：

 public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ret = new LinkedList<>();if(root == null){return ret;}ret.add(root.val);if(root.left!=null){List<Integer> leftList = preorderTraversal(root.left);ret.addAll(leftList);}if(root.right!=null){List<Integer> rightList = preorderTraversal(root.right);ret.addAll(rightList);}return ret;}

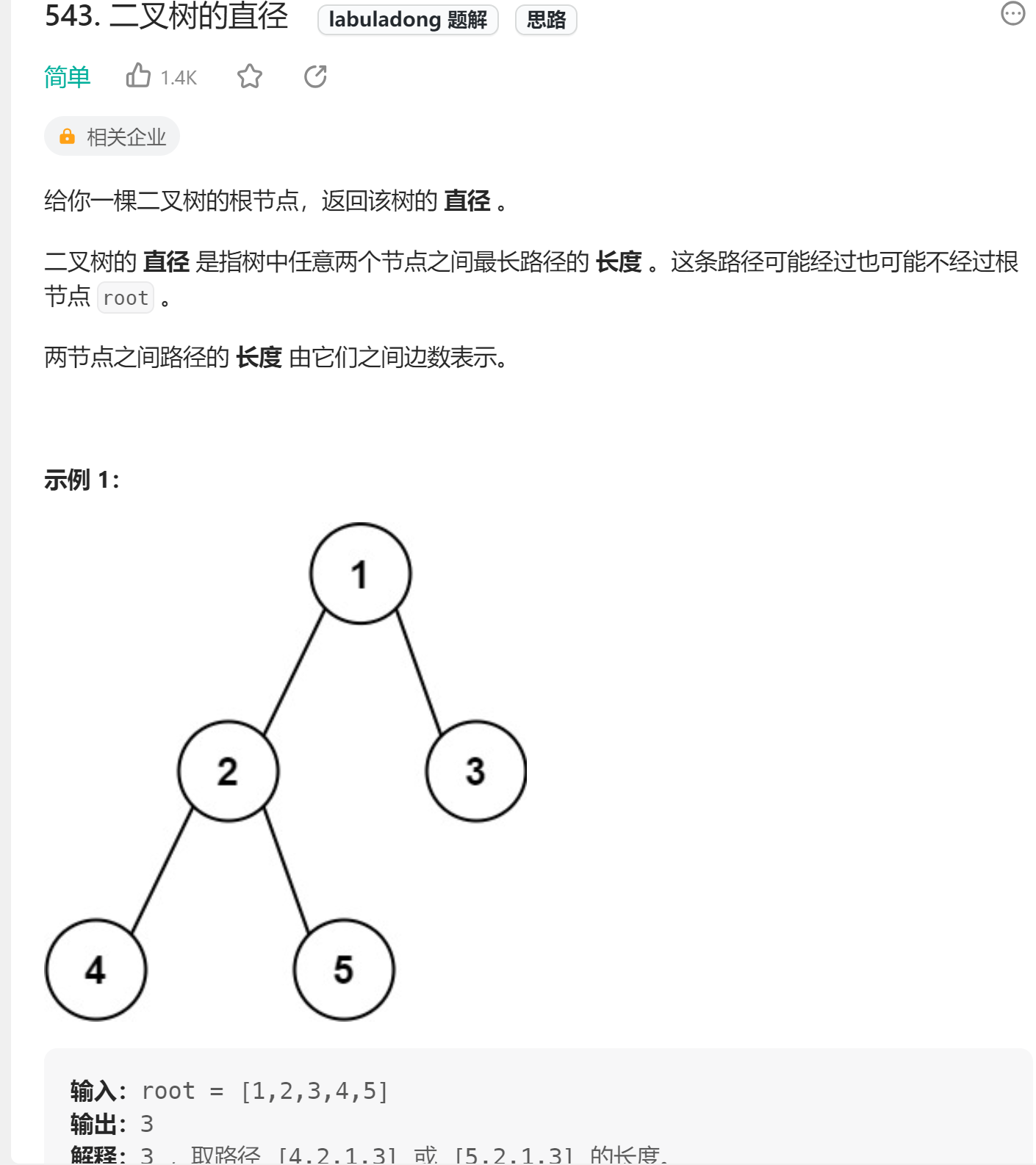
3、二叉树的直径

🔗543. 二叉树的直径
在这里插入图片描述

👧🏻思路：两种模式的结合，首先大的背景是利用maxDepth进行二叉树的后序遍历+求当前节点左右子树的最大高度.注意需要一个外部变量maxDiameter来时刻更新最大直径。（这种思路是O(n)的时间复杂度，可以用遍历每个节点+求当前节点的最大直径，思路是一样的，但是复杂度度是O(n2)，因为在本方法中在求maxDepth的时候就已经顺带遍历了整个节点！）

🙇🏻‍♀️代码：

	public int maxDiameter;public int diameterOfBinaryTree(TreeNode root) {maxDepth(root);return maxDiameter;}public int maxDepth(TreeNode root) {if(root == null){return 0;}//计算当前节点的左子树最大高度int leftH = maxDepth(root.left);//计算当前节点的右子树的最大高度int rightH = maxDepth(root.right);maxDiameter = Math.max(maxDiameter,leftH + rightH);//更新maxDiameterreturn 1 + Math.max(leftH, rightH);}