主线剧情-番外01-ARM系列快速鸟瞰

本文主要是介绍主线剧情-番外01-ARM系列快速鸟瞰，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

ARM & SOC 系列快速鸟瞰

编辑整理 By Staok，如有错误恭谢指出，侵删。CC-BY-NC-SA 4.0。

零鸟瞰

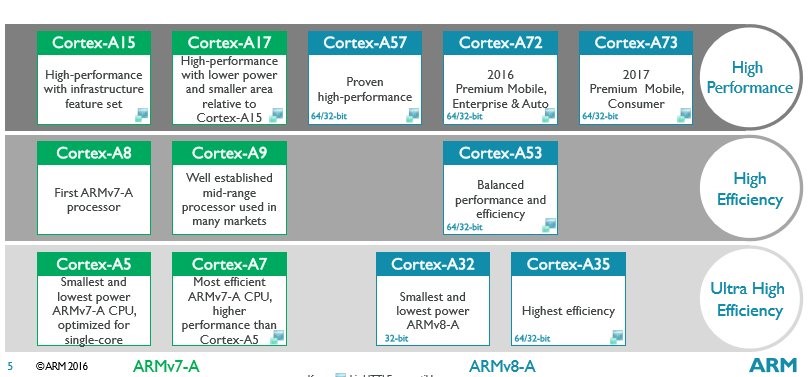
ARM Cortex 系列框图

图中包含现今主流处理器架构和内核层，ARM架构处理器的架构层、内核层和具体芯片（举例）三个维度的进化/迭代示意。

其中 “架构层” 属于指令集，代代扩展和丰富；“微架构” 是指指令集在处理器内部的具体的硬件电路实现，同一套指令集可以设计出多种微架构，即在架构（指令、数据分离等）、流水线（或超流水线）、Cache 分级情况、分支预测、乱序执行、SIMD、单发射/多发射、超线程等上的组合/配置的不同，构建不同的内核，即下文的 “内核层” 的区别，分出面向高性能、能耗平衡或低功耗的配置，微架构也称为处理器内核；在得到 ARM 公司的某个指令集或微架构的授权后，基于该内核在总线上挂载/集成各种 IP 外设，即搭建出具体的芯片，也叫片上系统（SoC），即下文的 “具体芯片层（举例）”。

ARM 体系结构的几大分类

ARM7 处理器；
ARM9、ARM9E 处理器；
ARM10E 处理器；
SecurCore 处理器；
StrongARM 处理器；
ARM11 处理器；
Cortex 系列处理器。

一定位

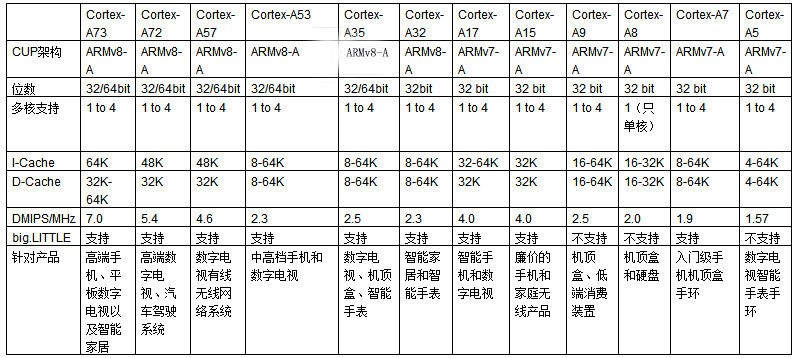
ARM Cortex-A 系列对比

更详细的介绍参看：

ARM Cortex-A系列处理器性能分类比较ARM处理器排名_ZNDS资讯
ARM版本系列及家族成员梳理_ 韦东山嵌入式专栏-CSDN博客 _arm系列
哪种ARM Cortex内核更适合我的应用：A系列、R系列、还是M系列？_water1730的博客-CSDN博客
ARMCortex各系列处理器分类比较 - 百度文库 (baidu.com)

引用：

如图所示，绿色的部分都是v7-A的架构，蓝色的是v8-A架构，基本上绿色都是可以支持到32和64位的，除了A32，只支持到32位。在右边的每个部分，比如说需要高效能的最上面的A15-A73这个部分是最高效的，接下来就是比较注重整个效率的部分了，中间那个部分是比较高效率的，最下面那栏的是效率最好的，在电池的效能方面达到了最好的标准。

如果非要给他们一个排序的话，从高到低大体上可排序为：Cortex-A73处理器、Cortex-A72处理器、Cortex-A57处理器、Cortex-A53处理器、Cortex-A35处理器、Cortex-A32处理器、Cortex-A17处理器、Cortex-A15处理器、Cortex-A7处理器、Cortex-A9处理器、Cortex-A8处理器、Cortex-A5处理器。