本文主要是介绍数据结构-栈应用(中缀转后缀并计算结果),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
关于中缀和后缀表达式基础概念自行百度。
对于中缀转后缀表达式并计算结果思路可归纳为以下:
1、将每个数据当做一个结构体,包含对应的类型以及数值;
2、对于给定的中缀表达式,转为结构体数组,进行后缀表达式的转换;
3、对于转换完成后的表达式进行计算,返回结果。
一、如何将中缀表达式转换为后缀表达式:
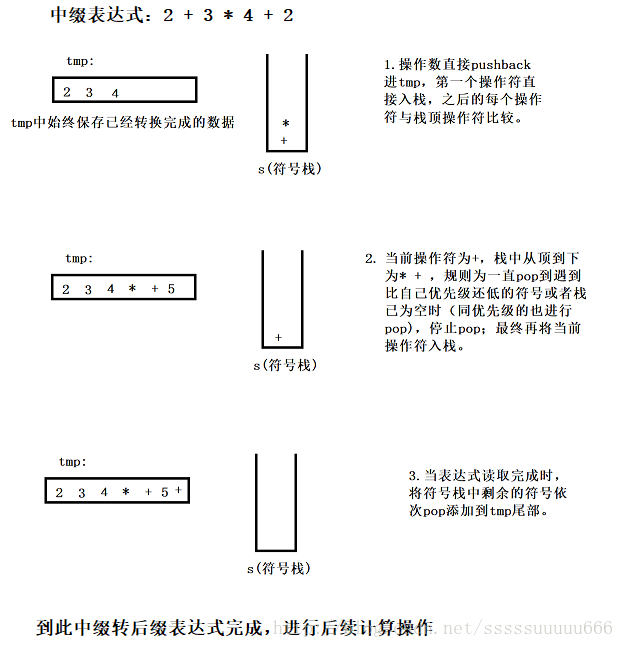
先给一个不涉及括号的中缀表达式,通过图简单缕一下转换到后缀表达式的方法:
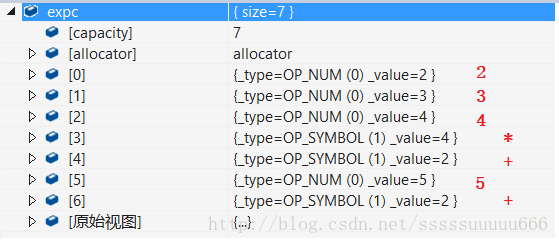
//2 + 3 * 4 + 5vector<Cell> arr = {{OP_NUM,2},{ OP_SYMBOL,OP_SUB },{ OP_NUM,3 },{ OP_SYMBOL,OP_MUL },{ OP_NUM,4 },{ OP_SYMBOL,OP_ADD },{ OP_NUM,5 },};转换完成后,可通过调试查看expc数组的元素值正如我们所画的那样:
但是在正常的简单运算中,不光只有加减乘除还有括号。在自己实现时可以先实现不带括号的转换过程,再按照带括号的转换规则进行稍微的修改即可。
转换原则:(对于自己实现的代码有所修改)
注:实现代码中的tmp数组始终保存的是已经完成中缀到后缀转换过程的操作数或操作符。
1.当读到一个操作数时,立即将它放到tmp数组中。第一个操作符则直接放入栈中。遇到左圆括号也入栈中;
2.如果遇到一个右括号,那么就将栈元素弹出,将符号转入tmp数组直到遇到一个对应的左括号。但是这个左括号只被弹出,并不转入tmp数组;
3.在读到操作符时,如果此时栈顶操作符优先性大于或等于此操作符,弹出栈顶操作符直到发现优先级更低的元素位置。除了处理)的时候,否则决不从栈中移走”(”。操作符中,+-优先级最低,()优先级最高。
4.如果读到输入的末尾,将栈元素弹出到tmp中,直到该栈变成空栈;
到此完成中缀到后缀的转换,转换后的结果重新拷贝回原expc数组,进行之后的运算。
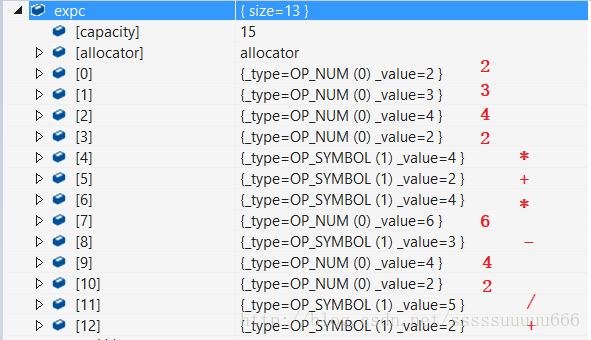
再附上一个带括号的中缀表达式转换:
可以复制代码到编译器中,自己一步一步调试查看过程。
中缀表达式:2 * ( 3 + 4 * 2 ) - 6 + 4 / 2
后缀表达式:2 3 4 2 * + * 6 - 4 2 / +
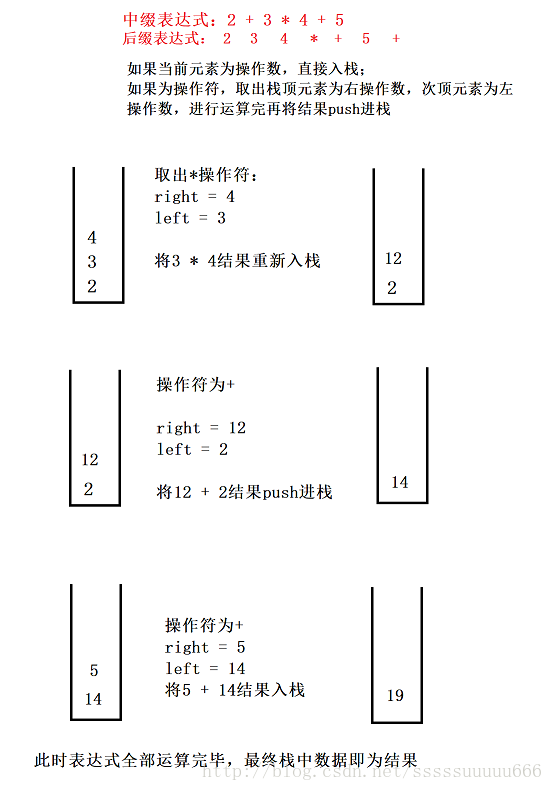
二、使用后缀表达式计算结果:
此时就只剩下了+,-,*,/四则运算;使用一开始的例子通过图来了解:
基本实现:
//RPN.h#pragma once#include <vector>
#include <stack>
#include <assert.h>
using namespace std;enum OP_TYPE
{OP_NUM, //操作数OP_SYMBOL, //操作符OP_ADD, //加法 2OP_SUB, //减法 3 OP_MUL, //乘法 4OP_DIV, //除法 5OP_LBAC, //左括号 6 OP_RBAC //右括号 7//...
};//数据单元 每一个数据分成两部分
struct Cell
{OP_TYPE _type;int _value;
};class RPN
{
public://给定中缀表达式转后缀RPN(vector<Cell>& expc, size_t n){//1.中缀转后缀之后MidToLast(expc,n);//2.拷贝到_rpnsize_t count = expc.size();for (size_t i = 0; i < count; i++)_rpn.push_back(expc[i]);}//中缀转后缀函数void MidToLast(vector<Cell>& expc,size_t n){stack<Cell> s;vector<Cell> tmp;for (size_t i = 0; i < n; i++){//如果遇到操作数,我们就直接将其输出。if (expc[i]._type == OP_NUM){tmp.push_back(expc[i]);}//操作符分情况讨论else if (expc[i]._type == OP_SYMBOL){if (!s.empty()){//如果是+ - ,则一直pop,除非遇到空或遇到左括号if (expc[i]._value == OP_ADD || expc[i]._value == OP_SUB){while (!s.empty() && s.top()._value != OP_LBAC){tmp.push_back(s.top());s.pop();}s.push(expc[i]);}//乘除运算符:else if (expc[i]._value == OP_MUL || expc[i]._value == OP_DIV){while (s.top()._value != OP_ADD && s.top()._value != OP_SUB && s.top()._value != OP_LBAC && !s.empty()){tmp.push_back(s.top());s.pop();}s.push(expc[i]);}//左括号直接入栈else if (expc[i]._value == OP_LBAC){s.push(expc[i]);}//如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。注意,左括号只弹出并不入tmp。else if (expc[i]._value == OP_RBAC){while (s.top()._value != OP_LBAC && !s.empty()){tmp.push_back(s.top());s.pop();}//左括号不入s.pop();}elseassert(false);}else{//符号栈为空,直接入符号s.push(expc[i]);}}elseassert(false);}//如果我们读到了输入的末尾,则将栈中所有元素依次弹出。* /while (!s.empty()){tmp.push_back(s.top());s.pop();}//将转为后缀的表达式拷贝回expcfor (size_t i = 0; i < tmp.size(); i++){expc[i] = tmp[i];}expc.resize(tmp.size());}int count(){stack<int> s; //计算时存放数据的栈for (size_t i = 0; i < _rpn.size();i++){if (_rpn[i]._type == OP_NUM){s.push(_rpn[i]._value);}else if (_rpn[i]._type == OP_SYMBOL){int right = s.top();s.pop();int left = s.top();s.pop();switch (_rpn[i]._value){case OP_ADD:s.push(left + right);break;case OP_SUB:s.push(left - right);break;case OP_MUL:s.push(left * right);break;case OP_DIV:s.push(left / right);break;default:assert(false);break;}}elseassert(false);}return s.top();}
private:vector<Cell> _rpn; //存后缀表达式
};
如发现问题请及时联系我谢谢~
这篇关于数据结构-栈应用(中缀转后缀并计算结果)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!