打击犯罪【并查集】

本文主要是介绍打击犯罪【并查集】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

打击犯罪

题目大意：

有n个人，相互之间有一些关系，从而形成一个图，现在要从$1\dots \dots n$按顺序去掉k个人（即去掉$1\dots \dots k$），使最大的子图的点数 $<n/2$，求k的最小值

原题：

题目描述

某个地区有n(n<=1000)个犯罪团伙，当地警方按照他们的危险程度由高到低给他们编号为1-n，他们有些团伙之间有直接联系，但是任意两个团伙都可以通过直接或间接的方式联系，这样这里就形成了一个庞大的犯罪集团，犯罪集团的危险程度唯一由集团内的犯罪团伙数量确定，而与单个犯罪团伙的危险程度无关（该犯罪集团的危险程度为n）。现在当地警方希望花尽量少的时间（即打击掉尽量少的团伙），使得庞大的犯罪集团分离成若干个较小的集团，并且他们中最大的一个的危险程度不超过n/2。为达到最好的效果，他们将按顺序打击掉编号1到k的犯罪团伙，请编程求出k的最小值。

如下图所示，打击掉1号团伙便能达到目的。

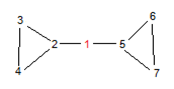
输入

第一行一个正整数n。
接下来的n行每行有若干个正整数，第一个整数表示该行除第一个外还有多少个整数，若第i行存在正整数k，表示i，k两个团伙可以直接联系。

输出

一个正整数，为k的最小值

输入样例

  72 2 53 1 3 42 2 42 2 33 1 6 72 5 72 5 6

输出样例

1

解题思路：

因为要按顺序，所以我们倒着用并查集加入每一个点，然后看每一个子图是否符合，当全部符合时继续，否则就输出

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#define max(a,b) (a)>(b)?(a):(b)
#define min(a,b) (a)<(b)?(a):(b)
using namespace std;
int n,xx,yy,k,a[1005][1005],dad[1005],b[1005];
int find(int dep){return dad[dep]==dep?dep:dad[dep]=find(dad[dep]);}//并查集
void lj(int x,int y)
{xx=find(x);yy=find(y);dad[min(xx,yy)]=max(xx,yy);//连接两个点
}
int main()
{scanf("%d",&n);for (int i=1;i<=n;++i){scanf("%d",&a[i][0]);for (int j=1;j<=a[i][0];++j)scanf("%d",&a[i][j]);}for (int i=1;i<=n;++i)dad[i]=i;int i=n+1;while (!k){i--;for (int j=1;j<=a[i][0];++j)if (a[i][j]>=i) lj(i,a[i][j]);//插入点memset(b,0,sizeof(b));for (int j=i;j<=n;++j)b[find(j)]++;//累加for (int j=i;j<=n;++j){if (b[j]>n/2)//判断{k=1;//不符合break;}}}printf("%d",i);
}

这篇关于打击犯罪【并查集】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---