本文主要是介绍深度强化学习(王树森)笔记06,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
深度强化学习(DRL)
本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。
参考链接
Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL
源代码链接:https://github.com/DeepRLChinese/DeepRL-Chinese
B站视频:【王树森】深度强化学习(DRL)
豆瓣: 深度强化学习
文章目录
- 深度强化学习(DRL)
- 蒙特卡洛估计
- 例一:近似 π \pi π 值
- 例二:估算阴影部分面积
- 例三:近似定积分
- 例四:近似期望
- 例五:随机梯度
- 总结
- 后记
蒙特卡洛估计
ChatGPT对蒙特卡洛方法的介绍
蒙特卡洛方法是一类基于随机抽样和统计学原理的数值计算方法,其核心思想是通过随机抽样来近似解决问题。这种方法在强化学习、优化问题、概率估计等领域都有广泛的应用。以下是关于蒙特卡洛方法的一些基本概念:
- 基本思想
- 随机抽样: 蒙特卡洛方法利用随机抽样的方式来近似计算某个问题的数值解。通过大量的随机样本,可以得到对问题的概率分布、期望值等进行估计的结果。
- 应用领域
-
强化学习: 在强化学习中,蒙特卡洛方法用于估计状态值、动作值,以及计算策略的期望回报。通过采样多条轨迹,可以近似地计算期望值。
-
数值积分: 蒙特卡洛方法可以用于估计复杂函数的积分值。通过在函数定义域内随机采样,计算函数值的平均值,可以得到积分的近似值。
-
概率估计: 蒙特卡洛方法在概率估计中也有应用,例如通过采样估计随机变量的期望、方差等统计量。
-
算法步骤
-
随机抽样: 根据问题的特性,通过随机抽样生成一系列样本点。
-
计算统计量: 对每个样本点进行计算,得到需要估计的统计量,例如期望值、方差等。
-
平均估计: 对所有样本点计算的统计量进行平均,得到最终的近似解。
-
-
优缺点
-
优点: 蒙特卡洛方法是一种通用的数值计算方法,对于复杂问题具有很强的适应性。它不依赖于问题的具体形式,而是通过随机抽样来逼近解。
-
缺点: 收敛速度相对较慢,特别是在维度较高的问题中,需要大量的样本才能获得准确的估计。同时,对于一些问题,可能存在抽样偏差。
总体而言,蒙特卡洛方法是一种强大的数值计算工具,尤其在面对复杂、高维度的问题时显示出其优越性。
蒙特卡洛(Monte Carlo) 是一大类随机算法 (randomized algorithms) 的总称,它们通过随机样本来估算真实值。本节用几个例子讲解蒙特卡洛算法。
例一:近似 π \pi π 值
我们都知道圆周率 π \pi π 约等于 3.1415927。现在假装我们不知道 π, 而是要想办法近似估算 π \pi π 值。假设我们有 (伪) 随机数生成器,我们能不能用随机样本来近似 π 呢?这一小节讨论使用蒙特卡洛如何近似 π \pi π 值。
假设我们有一个 (伪)随机数生成器,可以均匀牛成 -1 到 +1 之间的数。每次生成两个随机数,一个作为 x x x,另一个作为 y y y。于是每次生成了一个平面坐标系中的点 ( x , y ) (x,y) (x,y) , 见图 2.3(左)。因为 x x x 和 y y y 都是在 [-1,1] 区间 上均匀分布,所 [ − 1 , 1 ] × [ − 1 , 1 ] [-1,1]\times[-1,1] [−1,1]×[−1,1] 这个正方形内的点被抽到的概率是相同的。我们重复抽样 n n n 次,得到了 n n n 个正方形内的点。

如图2.3(右)所示,蓝色正方形里面包含一个绿色的圆,圆心是(0,0),半径等于1。刚才随机生成的 n n n个点有些落在圆外面,有些落在圆里面。
请问一个点落在圆里面的概率有多大呢?
由于抽样是均匀的,因此这个概率显然是圆的面积与正方形面积的比值。正方形的面积是边长的平方,即 a 1 = 2 2 = 4 a_1=2^2=4 a1=22=4。圆的面积是 π \pi π 乘以半径的平方,即 a 2 = π × 1 2 = π a_{2}=\pi\times1^{2}=\pi a2=π×12=π。 那么一个点落在圆里面的概率就是
p = a 2 a 1 = π 4 . p\:=\:\frac{a_{2}}{a_{1}}\:=\:\frac{\pi}{4}. p=a1a2=4π.
设我们随机抽样了 n n n个点,设圆内的点的数量为随机变量 M M M。显然, M M M 的期望等于
E [ M ] = p n = π n 4 . \mathbb{E}\big[M\big]\:=\:pn\:=\:\frac{\pi n}{4}. E[M]=pn=4πn.
注意,这只是期望,并不是实际发生的结果。如果你抽 n = 5 n=5 n=5个点,那么期望有 E [ M ] = 5 π 4 \mathbb{E}[M]=\frac{5\pi}4 E[M]=45π 个点落在圆内。但实际观测值 m m m 可能等于 0、1、2、3、4、5 中的任何一个。
给定一个点的坐标 ( x , y ) (x,y) (x,y),如何判断该点是否在圆内呢?已知圆心在原点,半径等于1,我们用一下圆的方程。如果 ( x , y ) (x,y) (x,y) 满足:
x 2 + y 2 ≤ 1 , x^2+y^2\:\leq\:1, x2+y2≤1,
则说明 ( x , y ) (x,y) (x,y) 落在圆里面;反之,点就在圆外面。
我们均匀随机抽样得到 n n n个点,通过圆的方程对每个点做判别,发现有 m m m 个点落在圆里面。如果 n n n 非常大,那么随机变量 M M M 的真实观测值 m m m 就会非常接近期望 E [ M ] = π n 4 E[M]=\frac{\pi n}4 E[M]=4πn:
m ≈ π n 4 . m\:\approx\:\frac{\pi n}{4}. m≈4πn.
由此得到:
π ≈ 4 m n . \pi\approx\frac{4m}n. π≈n4m.
我们可以依据这个公式做编程实现。下面是伪代码:
- 初始化 m = 0 m=0 m=0。用户指定样本数量 n n n 的大小。 n n n 越大,精度越高,但是计算量越大。
- 把下面的步骤重复 n n n 次:
(a). 从区间[-1,1]上做两次均匀随机抽样得到实数 x x x 和 y y y。
(b). 如果 x 2 + y 2 ≤ 1 x^2+y^2\leq1 x2+y2≤1, 那么 m ← m + 1 m\leftarrow m+1 m←m+1。
- 返回 4 m n \frac{4m}{n} n4m 作为对 π \pi π 的估计。
大数定律保证了蒙特卡洛的正确性:当 n n n 趋于无穷, 4 m n \frac{4m}n n4m 趋于 π \pi π。其实还能进一步用概率不等式分析误差的上界。比如使用 Bernstein 不等式,可以证明出下面结论:
∣ 4 m n − π ∣ = O ( 1 n ) . \left|\frac{4m}{n}-\pi\right|=O\Big(\frac{1}{\sqrt{n}}\Big). n4m−π =O(n1).
这个不等式说明 4 m n \frac{4m}n n4m (即对 π \pi π 的估计) 会收敛到 π \pi π, 收敛率是 1 n \frac1{\sqrt n} n1。然而这个收敛率并不快:样本数量 n n n 增加一万倍,精度才能提高一百倍。
例二:估算阴影部分面积
图2.4中有正方形、圆、扇形,几个形状相交。 请估算阴影部分面积。这个问题常见于初中数学竞赛。假如你不会微积分,也不会几何技巧,你是否有办法近似估算阴影部分面积呢?用蒙特卡洛可以很容易解决这个问题。
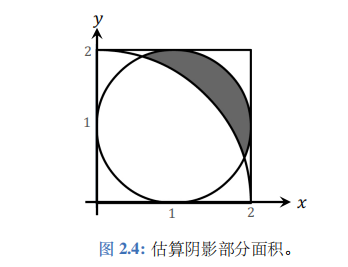
图 2.5 中绿色圆的圆心是 (1,1), 半径等于 1;蓝色扇形的圆心是 (0,0)、半径等于2。目的点 ( x , y ) (x,y) (x,y) 在绿色的圆中,而不在蓝色的扇形中。
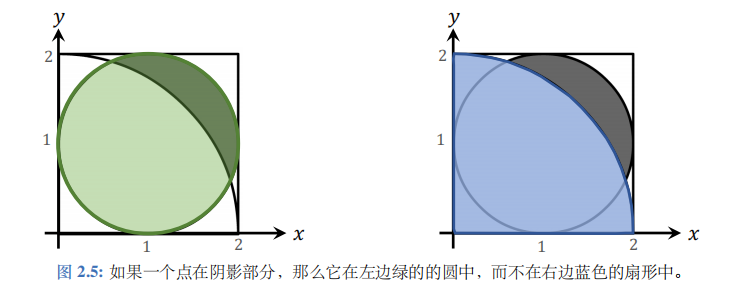
利用圆的方程可以判定点 ( x , y ) (x,y) (x,y) 是否在绿色圆里面。如果 ( x , y ) (x,y) (x,y) 满足方程
( x − 1 ) 2 + ( y − 1 ) 2 ≤ 1 , ( 2.1 ) (x-1)^2\:+\:(y-1)^2\:\leq\:1, \quad{(2.1)} (x−1)2+(y−1)2≤1,(2.1)
则说明 ( x , y ) (x,y) (x,y) 在绿色圆里面。
利用扇形的方程可以判定点 ( x , y ) (x,y) (x,y) 是否在蓝色扇形外面。如果点 ( x , y ) (x,y) (x,y) 满足方程
x 2 + y 2 > 2 2 , ( 2.2 ) x^{2}\:+\:y^{2}\:>\:2^{2},\quad{(2.2)} x2+y2>22,(2.2)
则说明 ( x , y ) (x,y) (x,y) 在蓝色扇形外面。
如果一个点同时满足方程 (2.1)和 (2.2), 那么这个点一定在阴影区域内。从 [ 0 , 2 ] × [ 0 , 2 ] [0,2]\times[0,2] [0,2]×[0,2] 这个正方形中做随机抽样,得到 n n n 个点。然后用两个方程筛选落在阴影部分的点。
我们在正方形 [ 0 , 2 ] × [ 0 , 2 ] [0,2]\times[0,2] [0,2]×[0,2] 中随机均匀抽样,得到的点有一定概率会落在阴影部分。我们来计算这个概率。正方形的边长等于2,所以面积 a 1 = 4 a_{1}=4 a1=4。设阴影部分面积为 a 2 a_{2} a2。那么点落在阴影部分概率是
p = a 2 a 1 = a 2 4 . p=\frac{a_2}{a_1}=\frac{a_2}{4}. p=a1a2=4a2.
我们从正方形中随机抽 n n n个点,设有 M M M 个点落在阴影部分内( M M M 是个随机变量)。每个点落在阴影部分的概率是 p p p,所以 M M M 的期望等于
E [ M ] = n p = n a 2 4 . \mathbb{E}[M]\:=\:np\:=\:\frac{na_{2}}{4}. E[M]=np=4na2.
用方程 (2.1)和 (2.2) 对 n n n 个点做筛选,发现实际上有 m m m 个点落在阴影部分内 ( m m m 是随机变量 M M M 的观测值)。如果 n n n 很大,那么 m m m 会比较接近期望 E [ M ] = n a 2 4 \mathbb{E}[M]=\frac{na_2}4 E[M]=4na2, 即
m ≈ n a 2 4 . m\:\approx\:\frac{na_{2}}{4}. m≈4na2.
也即:
a 2 ≈ 4 m n . a_{2}\approx\frac{4m}{n}. a2≈n4m.
这个公式就是对阴影部分面积的估计。我们依据这个公式做编程实现。下面是伪代码:
-
初始化 m = 0 m=0 m=0。用户指定样本数量 n n n 的大小。 n n n 越大,精度越高,但是计算量越大。
-
把下面的步骤重复 n n n 次:
(a). 从区间 [0,2] 上均匀随机抽样得到 x x x; 再做一次均匀随机抽样,得到 y y y。
(b). 如果 ( x − 1 ) 2 + ( y − 1 ) 2 ≤ 1 (x-1)^2+(y-1)^2\leq1 (x−1)2+(y−1)2≤1 和 x 2 + y 2 > 4 x^2+y^2>4 x2+y2>4 两个不等式都成立,那么让 m ← m + 1 。 m\leftarrow m+1_{\text{。}} m←m+1。 -
返回 4 m n \frac{4m}{n} n4m 作为对阴影部分面积的估计。
例三:近似定积分
近似求积分是蒙特卡洛最重要的应用之一,在科学和工程中有广泛的应用。举个例子,给定一个函数:
f ( x ) = 1 1 + ( sin x ) ⋅ ( ln x ) 2 , f(x)\:=\:\frac{1}{1+(\sin x)\cdot(\ln x)^2}, f(x)=1+(sinx)⋅(lnx)21,
要求计算 f f f 在区间 0.8 到 3 上的定积分:
I = ∫ 0.8 3 f ( x ) d x . I\:=\:\int_{0.8}^{3}f(x)\:d\:x. I=∫0.83f(x)dx.
有很多科学和工程问题需要计算定积分,而函数 f ( x ) f(x) f(x) 可能很复杂,求定积分会很困难, 甚至有可能不存在解析解。如果求解析解很困难,或者解析解不存在,则可以用蒙特卡洛近似计算数值解。
一元函数的定积分是相对比较简单的问题。一元函数的意思是变量 x x x 是个标量。给定一元函数 f ( x ) f(x) f(x), 求函数在 a a a 到 b b b 区间上的定积分:
I = ∫ a b f ( x ) d x . I\:=\:\int_{a}^{b}f(x)\:d\:x. I=∫abf(x)dx.
蒙特卡洛方法通过下面的步骤近似定积分:
1.在区间 [ a , b ] [a,b] [a,b] 上做随机抽样,得到 n n n 个样本,记作: x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn。样本数量 n n n 由用户自己定, n n n 越大,计算量越大,近似越准确。
- 对函数值 f ( x 1 ) , ⋯ , f ( x n ) f(x_1),\cdots,f(x_n) f(x1),⋯,f(xn) 求平均,再乘以区间长度 b − a : b-a: b−a:
q n = ( b − a ) ⋅ 1 n ∑ i = 1 n f ( x i ) . q_n\:=\:(b-a)\cdot\frac{1}{n}\sum_{i=1}^{n}f(x_i). qn=(b−a)⋅n1i=1∑nf(xi).
- 返回 q n q_n qn 作为定积分 I I I 的估计值。
多元函数的定积分要复杂一些。设 f : R d ↦ R f:\mathbb{R}^d\mapsto\mathbb{R} f:Rd↦R 是一个多元函数,变量 x x x 是 d d d 维向量。要求计算 f f f 在集合 Ω \Omega Ω 上的定积分:
I = ∫ Ω f ( x ) d x . I\:=\:\int_{\Omega}f(\boldsymbol{x})\:d\:\boldsymbol{x}. I=∫Ωf(x)dx.
蒙特卡洛方法通过下面的步骤近似定积分:
-
在集合 Ω 上做均匀随机抽样,得到 n n n 个样本,记作向量 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn。样本数量 n n n 由用户自己定, n n n 越大,计算量越大,近似越准确。
-
计算集合 Ω \Omega Ω 的体积: v = ∫ Ω d x . v=\int_\Omega d\boldsymbol{x}. v=∫Ωdx.
-
对函数值 f ( x 1 ) , ⋯ , f ( x n ) f(x_1),\cdots,f(x_n) f(x1),⋯,f(xn) 求平均,再乘以 Ω \Omega Ω 的体积 v v v:
q n = v ⋅ 1 n ∑ i = 1 n f ( x i ) . ( 2.3 ) q_{n}\:=\:v\cdot\frac{1}{n}\sum_{i=1}^{n}f(x_{i}). \quad{(2.3)} qn=v⋅n1i=1∑nf(xi).(2.3)
- 返回 q n q_n qn 作为定积分 I I I 的估计值。
注意,算法第二步需要求 Ω \Omega Ω 的体积。如果 Ω \Omega Ω 是长方体、球体等规则形状,那么可以解析地算出体积 v v v。可是如果 Ω \Omega Ω 是不规则形状,那么就需要定积分求 Ω \Omega Ω 的体积 v v v, 这是比较困难的。可以用类似于上一小节“求阴影部分面积”的方法近似计算体积 v v v。
举例讲解多元函数的蒙特卡洛积分:这个例子中被积分的函数是二元函数:
f ( x , y ) = { 1 , if x 2 + y 2 ≤ 1 ; 0 , otherwise . ( 2.4 ) \left.f\big(x,y\big)\:=\:\left\{\begin{array}{ll}1,&\text{if}\:x^2+y^2\leq1;\\0,&\text{otherwise}.\end{array}\right.\right. \quad{(2.4)} f(x,y)={1,0,ifx2+y2≤1;otherwise.(2.4)
直观地说,如果点 ( x , y ) (x,y) (x,y) 落在右图的绿色圆内,那么函数值就是 1; 否则函数值就是 0。定义集合 Ω = \Omega= Ω= [ − 1 , 1 ] × [ − 1 , 1 ] [-1,1]\times[-1,1] [−1,1]×[−1,1], 即右图中蓝色的正方形,它的面积是 v = 4 v=4 v=4。
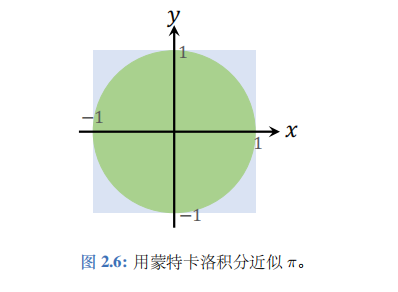
定积分
I = ∫ Ω f ( x , y ) d x d y I\:=\:\int_{\Omega}\:f\big(x,y\big)\:dx\:dy I=∫Ωf(x,y)dxdy
等于多少呢?很显然,定积分等于圆的面积,即 π ⋅ 1 2 = π \pi\cdot1^2=\pi π⋅12=π。因此,定积分 I = π I=\pi I=π。用蒙特卡洛求出 I I I,就得到了 π \pi π。从集合 Ω = [ − 1 , 1 ] × [ − 1 , 1 ] \Omega=[-1,1]\times[-1,1] Ω=[−1,1]×[−1,1]上均匀随机抽样 n n n 个点,记作 ( x 1 , y 1 ) , ⋯ , ( x n , y n ) (x_1,y_1),\cdots,(x_n,y_n) (x1,y1),⋯,(xn,yn)。应用公式(2.3), 可得
q n = v ⋅ 1 n ∑ i = 1 n f ( x i , y i ) = 4 n ∑ i = 1 n f ( x i , y i ) . ( 2.5 ) q_{n}\:=\:v\cdot\frac{1}{n}\sum_{i=1}^{n}f(x_{i},y_{i})\:=\:\frac{4}{n}\sum_{i=1}^{n}f(x_{i},y_{i}). \quad{(2.5)} qn=v⋅n1i=1∑nf(xi,yi)=n4i=1∑nf(xi,yi).(2.5)
把 q n q_n qn 作为对定积分 I = π I=\pi I=π 的近似。这与前面近似 π \pi π 的算法完全相同,区别在于此处的算法是从另一个角度推导出的。
例四:近似期望
蒙特卡洛还可以用来近似期望,这在整本书中会反复应用。设 X X X 是 d d d 维随机变量,它的取值范围是集合 Ω ⊂ R d \Omega\subset\mathbb{R}^d Ω⊂Rd。函数 p ( x ) p(\boldsymbol{x}) p(x) 是 X X X 的概率密度函数。设 f : Ω ↦ R f:\Omega\mapsto\mathbb{R} f:Ω↦R 是任意的多元函数,它关于变量 X X X 的期望是:
E X ∼ p ( ⋅ ) [ f ( X ) ] = ∫ Ω p ( x ) ⋅ f ( x ) d x . \mathbb{E}_{X\sim p(\cdot)}\Big[f(X)\Big]\:=\:\int_{\Omega}p(\boldsymbol{x})\cdot f(\boldsymbol{x})\:d\:\boldsymbol{x}. EX∼p(⋅)[f(X)]=∫Ωp(x)⋅f(x)dx.
由于期望是定积分,所以可以按照上一小节的方法,用蒙特卡洛求定积分。上一小节在集合 Ω \Omega Ω上做均匀抽样,用得到的样本近似上面公式中的定积分。
下面介绍一种更好的算法。既然我们知道概率密度函数 p ( x ) p(x) p(x), 我们最好是按照 p ( x ) p(x) p(x) 做非均匀抽样,而不是均匀抽样。按照 p ( x ) p(x) p(x) 做非均匀抽样,可以比均匀抽样有更快的收敛。具体步骤如下:
- 按照概率密度函数 p ( x ) p(x) p(x),在集合 Ω \Omega Ω 上做非均匀随机抽样,得到 n n n 个样本,记作向量 x 1 , ⋯ , x n ∼ p ( ⋅ ) x_1,\cdots,x_n\sim p(\cdot) x1,⋯,xn∼p(⋅)。样本数量 n n n 由用户自己定, n n n 越大,计算量越大;近似越准确。
- 对函数值 f ( x 1 ) , ⋯ , f ( x n ) f(x_1),\cdots,f(x_n) f(x1),⋯,f(xn) 求平均:
q n = 1 n ∑ i = 1 n f ( x i ) . q_{n}\:=\:\frac{1}{n}\sum_{i=1}^{n}f\left(x_{i}\right). qn=n1i=1∑nf(xi).
- 返回 q n q_n qn 作为期望 E X ∼ p ( ⋅ ) [ f ( X ) ] \mathbb{E}_{X\sim p(\cdot)}[f(X)] EX∼p(⋅)[f(X)] 的估计值。
注 如果按照上述方式做编程实现,需要储存函数值 f ( x 1 ) , ⋯ , f ( x n ) f(x_1),\cdots,f(x_n) f(x1),⋯,f(xn)。但用如下的方式做编程实现,可以减小内存开销。初始化 q 0 = 0 q_0=0 q0=0。从 t = 1 t=1 t=1 到 n n n,依次计算
q t = ( 1 − 1 t ) ⋅ q t − 1 + 1 t ⋅ f ( x t ) . ( 2.6 ) q_{t}\:=\:\left(1-\frac{1}{t}\right)\cdot q_{t-1}\:+\:\frac{1}{t}\cdot f\left(x_{t}\right). \quad{(2.6)} qt=(1−t1)⋅qt−1+t1⋅f(xt).(2.6)
不难证明,这样得到的 q n q_n qn 等于 1 n ∑ i = 1 n f ( x i ) \frac1n\sum_{i=1}^nf(x_i) n1∑i=1nf(xi)。这样无需存储所有的 f ( x 1 ) , ⋯ , f ( x n ) f(x_1),\cdots,f(x_n) f(x1),⋯,f(xn)。可以进一步把公式(2.6) 中的 1 t \frac1t t1 替换成 α t \alpha_t αt, 得到公式:
q t = ( 1 − α t ) ⋅ q t − 1 + α t ⋅ f ( x t ) . q_{t}\:=\:\left(1-\alpha_{t}\right)\cdot q_{t-1}\:+\:\alpha_{t}\cdot f(x_{t}). qt=(1−αt)⋅qt−1+αt⋅f(xt).
这个公式叫做 Robbins-Monro 算法,其中 α n \alpha_n αn 称为学习步长或学习率。只要 α t \alpha_t αt 满足下面的性质,就能保证算法的正确性:
lim n → ∞ ∑ t = 1 n α t = ∞ 和 lim n → ∞ ∑ t = 1 n α t 2 < ∞ . \lim_{n\to\infty}\:\sum_{t=1}^{n}\alpha_{t}\:=\:\infty\quad\text{和}\quad\lim_{n\to\infty}\:\sum_{t=1}^{n}\alpha_{t}^{2}\:<\:\infty. n→∞limt=1∑nαt=∞和n→∞limt=1∑nαt2<∞.
显然, α t = 1 t \alpha_t=\frac1t αt=t1 满足上述性质。Robbins-Monro 算法可以应用在 Q 学习算法中。
例五:随机梯度
我们可以用蒙特卡洛近似期望来理解随机梯度算法。
设随机变量 X X X 为一个数据样本,令 w w w 为神经网络的参数。设 p ( x ) p(\boldsymbol{x}) p(x) 为随机变量 X X X 的概率密度函数。定义损失函数 L ( X ; w ) L(X;\boldsymbol{w}) L(X;w)。它的值越小,意味着模型做出的预测越准确;反之,它的值越大,则意味着模型做出的预测越差。因此,我们希望调整神经网络的参数 w w w, 使得损失函数的期望尽量小。神经网络的训练可以定义为这样的优化问题:
min w E X ∼ p ( ⋅ ) [ L ( X ; w ) ] . \min_{\boldsymbol{w}}\:\mathbb{E}_{X\sim p(\cdot)}\Big[L(X;\boldsymbol{w})\Big]. wminEX∼p(⋅)[L(X;w)].
目标函数 E X [ L ( X ; w ) ] \mathbb{E}_X[L(X;\boldsymbol{w})] EX[L(X;w)] 关于 w w w 的梯度是:
g ≜ ∇ w E X ∼ p ( ⋅ ) [ L ( X ; w ) ] = E X ∼ p ( ⋅ ) [ ∇ w L ( X ; w ) ] . ( 2.7 ) \boldsymbol{g}\triangleq\:\nabla_{\boldsymbol{w}}\mathbb{E}_{X\sim p(\cdot)}\Big[\:L(X;\boldsymbol{w})\:\Big]\:=\:\mathbb{E}_{X\sim p(\cdot)}\Big[\:\nabla_{\boldsymbol{w}}\:L(X;\boldsymbol{w})\:\Big]. \quad{(2.7)} g≜∇wEX∼p(⋅)[L(X;w)]=EX∼p(⋅)[∇wL(X;w)].(2.7)
可以做梯度下降更新 w w w, 以减小目标函数 E X [ L ( X ; w ) ] \mathbb{E}_X[L(X;\boldsymbol{w})] EX[L(X;w)]:
w ← w − α ⋅ g . w\gets w-\alpha\cdot g. w←w−α⋅g.
此处的 α \alpha α被称作学习率 (learning rate)。直接计算梯度 g g g 通常会比较慢。为了加速计算, 可以对期望
g = E X ∼ p ( ⋅ ) [ ∇ w L ( X ; w ) ] g=\mathbb E_{X\sim p(\cdot)}\Big[\nabla_{\boldsymbol{w}}L(X;\boldsymbol{w})\Big] g=EX∼p(⋅)[∇wL(X;w)]
做蒙特卡洛近似,把得到的近似梯度 g ~ \tilde{g} g~ 称作随机梯度 (stochastic gradient), 用 g ~ \tilde{g} g~ 代替 g g g 来更新 w w w。
- 根据概率密度函数 p ( x ) p(\boldsymbol{x}) p(x) 做随机抽样,得到 B B B 个样本,记作 x ~ 1 , … , x ~ B \tilde{x}_1,\ldots,\tilde{x}_B x~1,…,x~B。
- 计算梯度 ∇ w L ( x ~ j ; w ) \nabla_{\boldsymbol{w}}L(\tilde{\boldsymbol{x}}_j;\boldsymbol{w}) ∇wL(x~j;w), ∀ j = 1 , … , B \forall j=1,\ldots,B ∀j=1,…,B。对它们求平均:
g ~ = 1 B ∑ j = 1 B ∇ w L ( x ~ j ; w ) . \tilde{\boldsymbol{g}}\:=\:\frac{1}{B}\sum_{j=1}^{B}\nabla_{\boldsymbol{w}}L(\tilde{\boldsymbol{x}}_{j};\boldsymbol{w}). g~=B1j=1∑B∇wL(x~j;w).
我们称 g ~ \tilde{g} g~ 为随机梯度。因为 E [ g ~ ] = g \mathbb{E}[\tilde{g}]=g E[g~]=g,它是 g g g 的一个无偏估计。
3. 做随机梯度下降更新 w : w: w:
w ← w − α ⋅ g ~ . w\:\leftarrow\:w\:-\:\alpha\cdot\tilde{\boldsymbol{g}}. w←w−α⋅g~.
样本数量 B B B 称作批量大小 (batch size), 通常是一个比较小的正整数,比如 1、8、16、32。所以我们称之为最小批 (mini-batch) SGD。
在实际应用中,样本真实的概率密度函数 p ( x ) p(\boldsymbol{x}) p(x) 一般是未知的。在训练神经网络的时候,我们通常会收集一个训练数据集 X = { x 1 , ⋯ , x n } X=\{x_1,\cdots,x_n\} X={x1,⋯,xn}, 并求解这样一个经验风险最小化 (empirical risk minimization) 问题:
min w 1 n ∑ i = 1 n L ( x i ; w ) . ( 2.8 ) \min_{\boldsymbol{w}}\:\frac{1}{n}\sum_{i=1}^{n}L(\boldsymbol{x}_{i};\boldsymbol{w}).\quad{(2.8)} wminn1i=1∑nL(xi;w).(2.8)
这相当于我们用下面这个概率质量函数代替真实的 p ( x ) : p(x): p(x):
p ( x ) = { 1 n , 如果 x ∈ X ; 0 , 如果 x ∉ X . \left.p(\boldsymbol{x})\:=\:\left\{\begin{array}{ll}\frac{1}{n},&\text{如果 }x\in\mathcal{X};\\0,&\text{如果 }x\not\in\mathcal{X}.\end{array}\right.\right. p(x)={n1,0,如果 x∈X;如果 x∈X.
公式的意思是随机变量 X X X 的取值是 n n n 个数据点中的一个,概率都是 1 n \frac1n n1。那么最小批 SGD 的每一轮都从集合 { x 1 , ⋯ , x n } \{x_1,\cdots,x_n\} {x1,⋯,xn} 中均匀随机抽取 B B B 个样本,计算随机梯度,更新模型参数 w ∘ w_{\circ} w∘
总结
本文详细讲解了蒙特卡洛的应用。其中最重要的知识点是蒙特卡洛近似期望:设 X X X 是随机变量, x x x 是观测值,蒙特卡洛用 f ( x ) f(x) f(x) 近似期望 E [ f ( X ) ] \mathbb{E}[f(X)] E[f(X)]。强化学习中的 Q 学习、SARSA、策略梯度等算法都需要这样用蒙特卡洛近似期望。
后记
截至2024年1月28日18点38分,完成Monte Carlo Algorithms这节的学习。主要学习用蒙特卡洛方法求随机梯度,对后续强化学习算法的学习有帮助。
这篇关于深度强化学习(王树森)笔记06的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



