本文主要是介绍即插即用,视频超分中的涨点神器:iSeeBetter,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

CNN让超分结果更真实,GAN让超分结果更丰满,所以CNN+GAN=GOOD!添加一个鉴别器组件就能使结果增加0.32dB,即插即用,涨点神器!是否在其他的CNN架构上也可行,还需实验验证。
论文:iSeeBetter:使用递归生成反投影网络的时空视频超分
代码:https://github.com/amanchadha/iSeeBetter
看点
CNN在大尺度上的超分往往缺乏精细的细节纹理,生成性对抗网络能够缓解这个问题。为此,本文提出了一种基于GAN的时空视频超分方法——iSeeBetter,亮点如下:
结合了SR中的SOTA技术: 使用循环反投影网络(RBPN)的作为其生成器,从当前帧和相邻帧中提取时空信息。使用SRGAN中的鉴别器,提高了超分辨率图像的“自然性”,减轻了传统算法中的伪影。
优化了损失函数的架构: 本文使用了四重损失函数(MSE、感知损失、对抗损失和全变差损失(TV))来捕捉均方误差(MSE)可能无法捕捉到的图像中的精细细节,加强生成视频的感知质量。

方法
下图展示了分别由RBPN和SRGAN作为生成器和鉴别器的iSeeBetter架构。
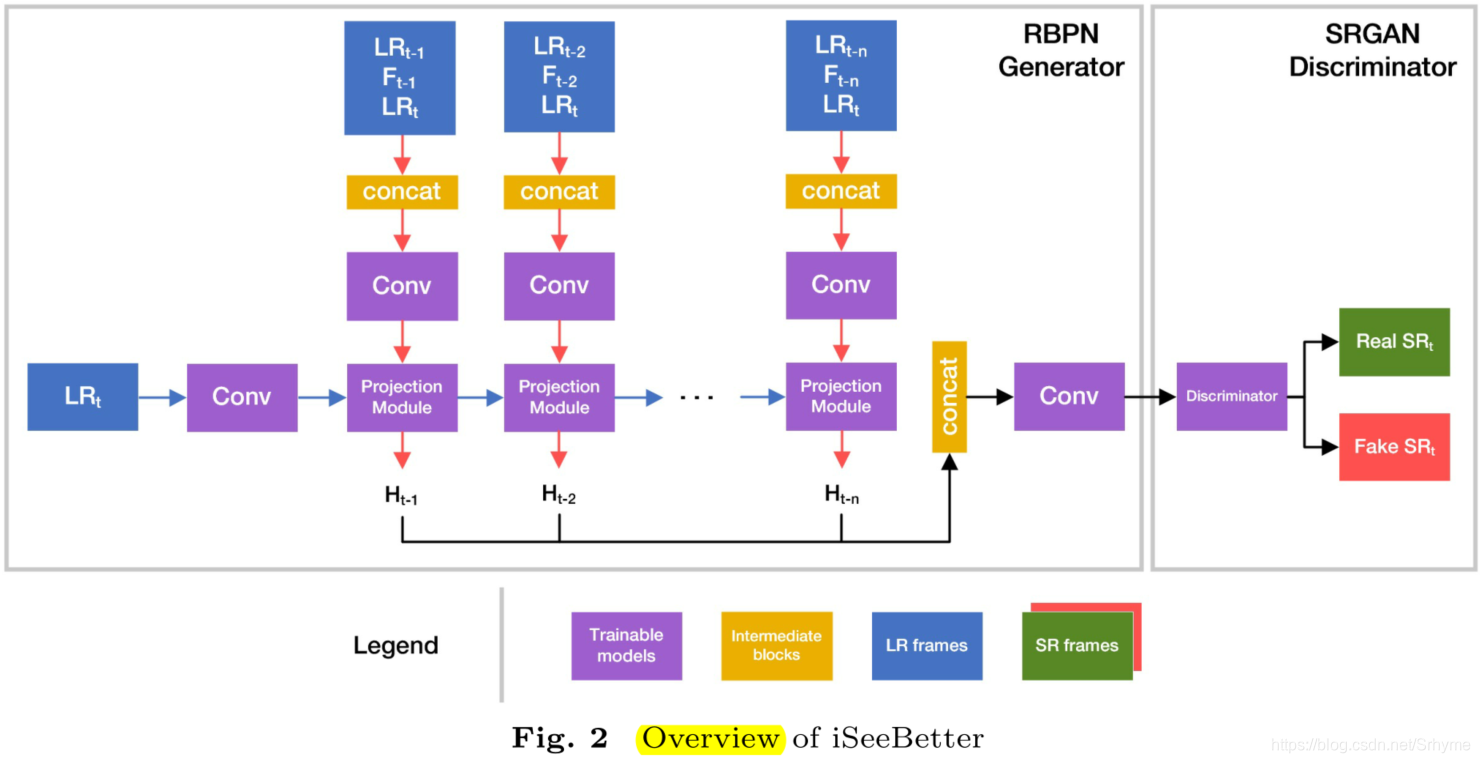
RBPN中的投影模块有两种从不同来源提取缺失细节的方法:SISR和MISR。下图展示了使用DBPN作为SISR结构的水平流(图2中的蓝色箭头)。
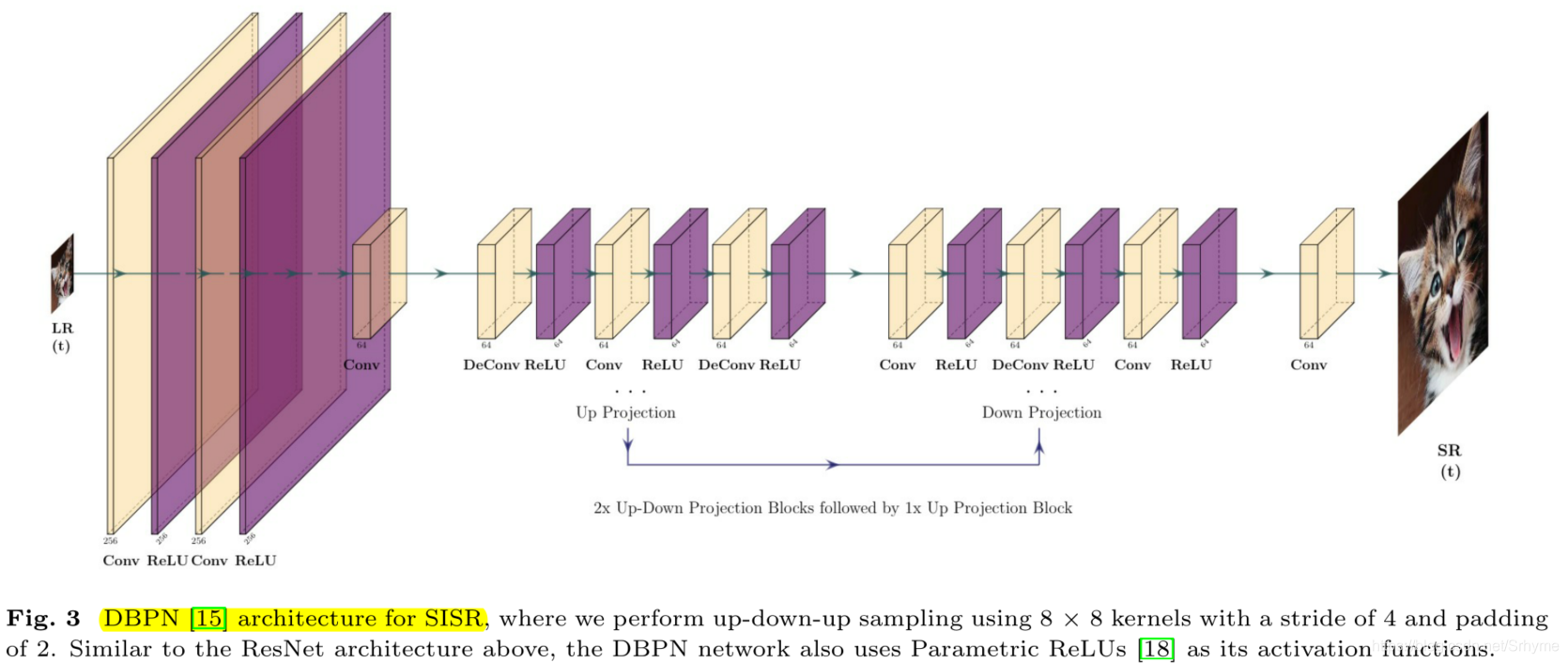
下图展示了使用五个残差块作为MISR结构的垂直流(图2中的红色箭头),MISR的输入由LR帧、相邻帧以及它们之间的密集动作流图组成。
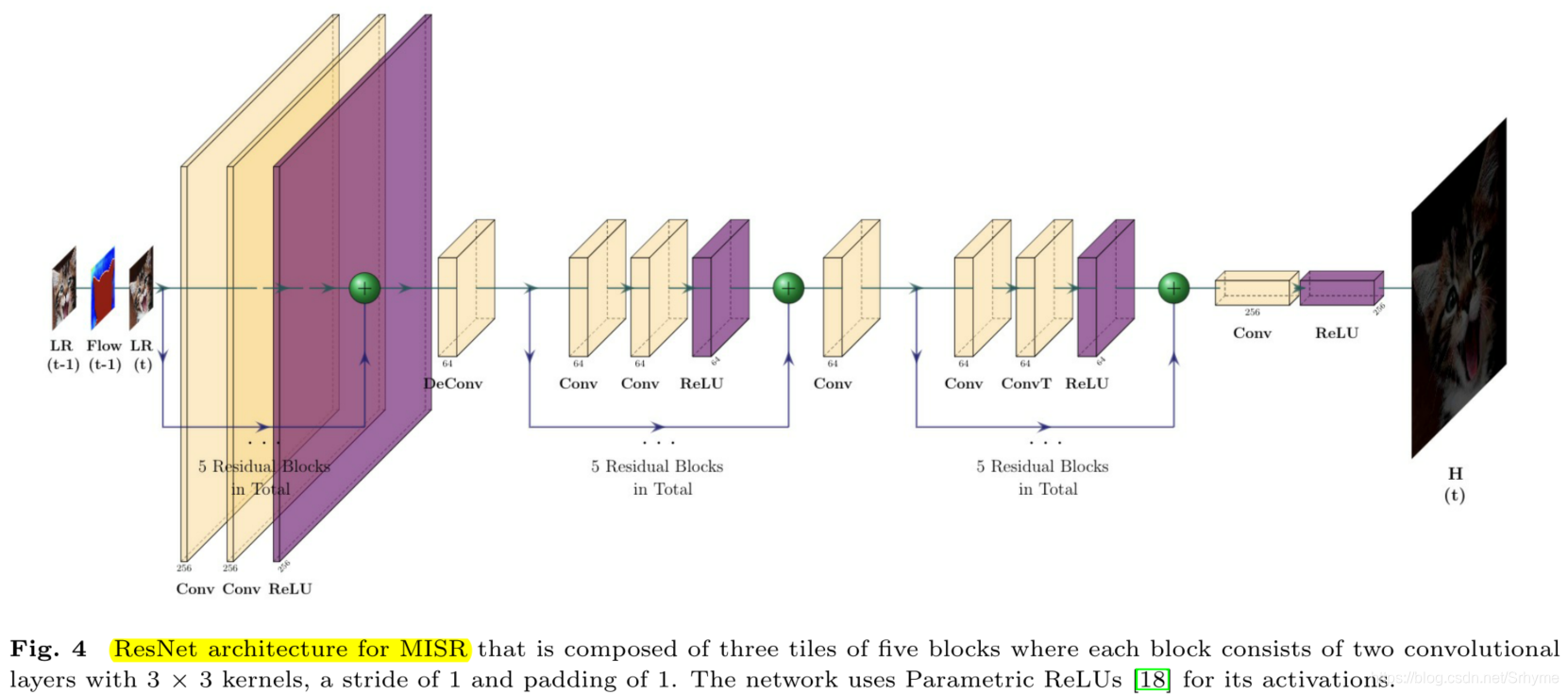
在每个投影中,RBPN观察LR中丢失的细节,并从相邻帧中提取残差特征来恢复细节。RBPN利用循环编解码机制来融合从SISR和MISR中提取的细节,并通过反投影将它们合并到SR帧中。一旦合成了SR帧,它就被到鉴别器中以验证其“真实性”,鉴别器采用SRGAN的鉴别器,结构如下图所示。
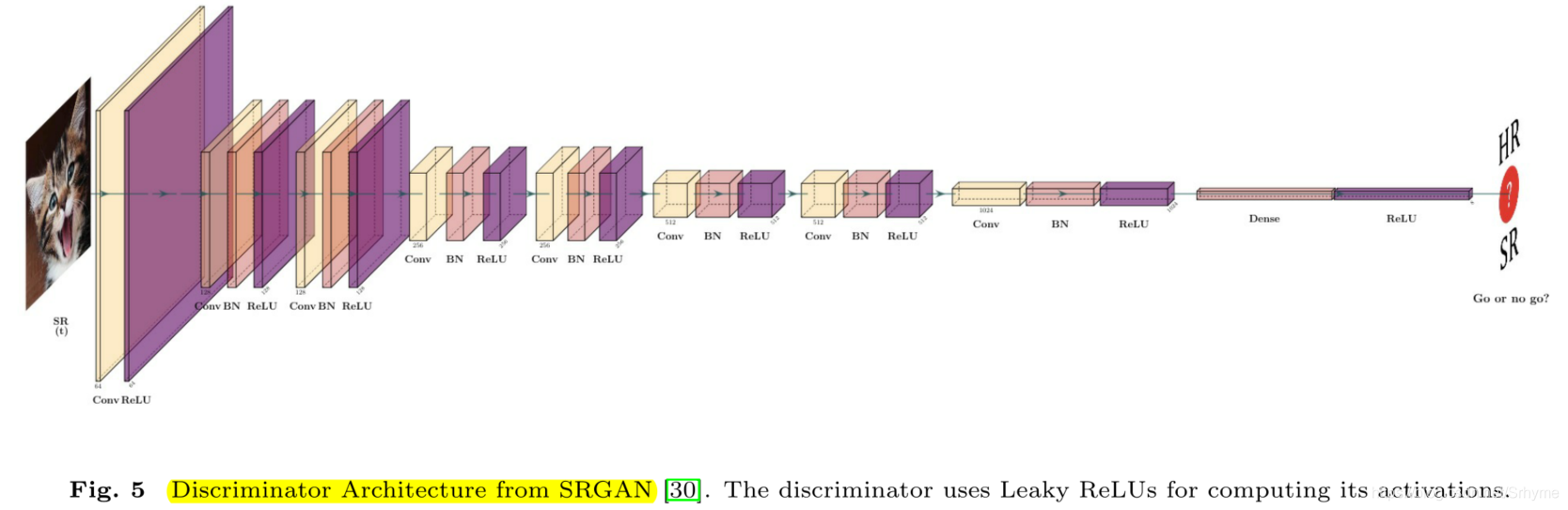
损失
生成的SR图像的感知质量取决于损失函数的选择。为了评估图像的质量,MSE是各种方法中最常用的损失函数,其目的是提高图像的PSNR。但是这可能无法捕获图像中的精细细节,从而影响感知质量。同时,MSE捕获复杂纹理细节的能力有限,生成的视频帧过于平滑。为了解决这些问题,iSeeBetter使用了四重损失,并将这些损失综合起来作为训练iSeeBetter的最终评估标准。
MSE损失
MSE损失也称内容损失,其中 G θ G ( L R t ) G_{θ_G}(LR_t) GθG(LRt)表示SR帧。
M S E t = 1 W H ∑ x = 0 W ∑ y = 0 H ( ( H R t ) x , y − G θ G ( L R t ) x , y ) 2 MSE_{t}=\frac{1}{W H} \sum_{x=0}^{W} \sum_{y=0}^{H}\left(\left(HR_{t}\right)_{x, y}-G_{\theta_{G}}\left(LR_{t}\right)_{x, y}\right)^{2} MSEt=WH1x=0∑Wy=0∑H((HRt)x,y−GθG(LRt)x,y)2
感知损失
感知损失定义为SR帧的特征表示 G θ G ( L R t ) G_{θ_G}(LR_t) GθG(LRt)与真实帧HR之间的欧氏距离。它关注的是感知相似性,而不是像素空间中的相似性。依赖于从VGG-19网络中提取的特征。
Perceptual Loss t = f r a c 1 W i , j H i , j ∑ x = 1 W i , j ∑ y = 1 H i , j ( V G G i , j ( H R t ) x , y − V G G i , j ( G θ G ( L R t ) ) x , y ) 2 \begin{aligned} &\text { Perceptual Loss }_{t}=frac{1}{W_{i, j} H_{i, j}} \sum_{x=1}^{W_{i, j}} \sum_{y=1}^{H_{i, j}}\left(\begin{array}{l} V G G_{i, j}\left(H R_{t}\right)_{x, y}- \\ V G G_{i, j}\left(G_{\theta_{G}}\left(L R_{t}\right)\right)_{x, y} \end{array}\right)^{2} \end{aligned} Perceptual Loss t=frac1Wi,jHi,jx=1∑Wi,jy=1∑Hi,j(VGGi,j(HRt)x,y−VGGi,j(GθG(LRt))x,y)2
其中 V G G i , j VGG_{i,j} VGGi,j表示第 i t h i^{th} ith个池化层之前 j t h j^{th} jth卷积激活后的特征图。
对抗损失
对抗损失限制模型的“幻想”,提高了超分辨图像的“自然性”。定义如下:
Adversarial Loss t = − log ( D θ D ( G θ G ( L R t ) ) \text { Adversarial } \operatorname{Loss}_{t}=-\log \left(D_{\theta_{D}}\left(G_{\theta_{G}}\left(L R_{t}\right)\right)\right. Adversarial Losst=−log(DθD(GθG(LRt))
其中, D θ D ( G θ G ( L R t ) ) D_{θ_D}(G_{θ_G}(LR_t)) DθD(GθG(LRt))是鉴别器认为生成图像是真实图像的输出概率。本文最小化 − l o g ( D θ D ( G θ G ( L R t ) ) ) -log(D_{\theta D}(G_{\theta G}(LR_{t}))) −log(DθD(GθG(LRt)))去获得更佳的梯度行为。
全变差损失
全变差损失定义为水平方向和垂直方向上相邻像素之间的绝对差之和。由于TV损失测量输入中的噪声,因此将其最小化作为总体损失目标的一部分有助于去除输出SR帧中的噪声,从而提高空间平滑度。定义如下:
T V Loss t = 1 W H ∑ i = 0 W ∑ j = 0 H ( G θ G ( L R t ) i , j + 1 , k − G θ G ( L R t ) i , j , k ) 2 + ( G θ G ( L R t ) i + 1 , j , k − G θ G ( L R t ) i , j , k ) 2 TV \operatorname{Loss}_{t}=\frac{1}{W H} \sum_{i=0}^{W} \sum_{j=0}^{H} \sqrt{\begin{array}{l} \left(G_{\theta_{G}}\left(L R_{t}\right)_{i, j+1, k}-G_{\theta_{G}}\left(L R_{t}\right)_{i, j, k}\right)^{2}+ \\ \left(G_{\theta_{G}}\left(L R_{t}\right)_{i+1, j, k}-G_{\theta_{G}}\left(L R_{t}\right)_{i, j, k}\right)^{2} \end{array}} TVLosst=WH1i=0∑Wj=0∑H(GθG(LRt)i,j+1,k−GθG(LRt)i,j,k)2+(GθG(LRt)i+1,j,k−GθG(LRt)i,j,k)2
总损失
生成器的总损失为上面四个损失的加权和,如下图所示:
Loss G θ G ( S R t ) = α × M S E ( S R t , H R t ) + β × Perceptual oss ( S R t , H R t ) + γ × Adversarial Loss ( S R t ) + δ × T VLoss ( S R t , H R t ) \operatorname{Loss}_{G_{\theta_{G}}}\left(S R_{t}\right)=\begin{aligned} \alpha & \times M S E\left(S R_{t}, H R_{t}\right) \\ +& \beta \times \text {Perceptual } \operatorname{oss}\left(S R_{t}, H R_{t}\right) \\ +& \gamma \times \text {Adversarial } \operatorname{Loss}\left(S R_{t}\right) \\ +& \delta \times T \operatorname{VLoss}\left(S R_{t}, H R_{t}\right) \end{aligned} LossGθG(SRt)=α+++×MSE(SRt,HRt)β×Perceptual oss(SRt,HRt)γ×Adversarial Loss(SRt)δ×TVLoss(SRt,HRt)
其中 α , β , γ , δ \alpha,\beta,\gamma,\delta α,β,γ,δ是权重,值分别为1, 6 × 1 0 − 3 6×10^{-3} 6×10−3, 1 0 − 3 10^{-3} 10−3, 2 × 1 0 − 8 2×10^{-8} 2×10−8。
鉴别器的总损失如下:
Loss D θ D ( S R t ) = 1 − D θ D ( H R t ) + D θ D ( S R t ) \operatorname{Loss}_{D_{\theta_{D}}}\left(S R_{t}\right)=1-D_{\theta_{D}}\left(H R_{t}\right)+D_{\theta_{D}}\left(S R_{t}\right) LossDθD(SRt)=1−DθD(HRt)+DθD(SRt)
实验
数据集
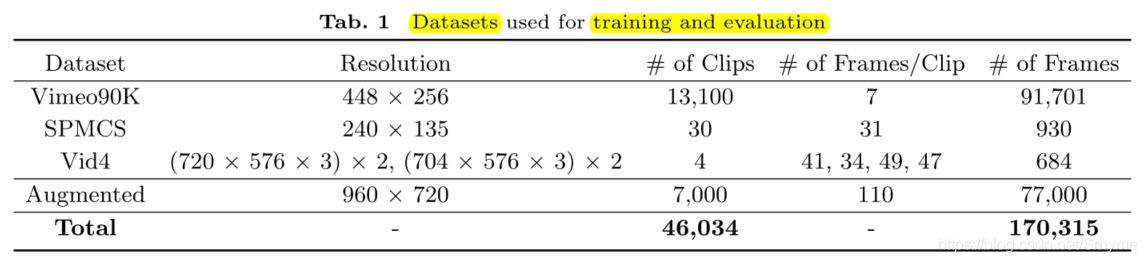
为了使iSebetter更加健壮,并使其能够处理真实世界的视频,作者从YouTube收集了额外的数据,将数据集扩充到大约170000个片段,训练/验证/测试分别为其中的80%/10%/10%。训练时采用BI的降质方式,下图展示了数据集的组成。
消融实验
对所提出的架构和损失函数进行消融实验:

量化评估

这篇关于即插即用,视频超分中的涨点神器:iSeeBetter的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








