信号处理中用DCT进行图像处理

本文主要是介绍信号处理中用DCT进行图像处理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

转自： http://blog.csdn.net/ahafg/article/details/48808443

DCT又称离散余弦变换，是一种块变换方式，只使用余弦函数来表达信号，与傅里叶变换紧密相关。常用于图像数据的压缩，通过将图像分成大小相等（一般为8*8）的块，利用DCT对其进行变换，得到更加简洁的数据。因为图像像素间存在较大的空间相关性，DCT可以大大减小这些相关性，使图像能量集中在左上角区域，从而利于数据压缩。变换后得到的数据称为DCT系数。这一过程是无损的。

二维DCT变换

这里来看看二维DCT变换的公式：

clear;
clc;
I = [12,23,53,16;42,16,68,45;34,62,73,26;72,15,34,28];  %数据块
A = zeros(4);   %变换矩阵A,也可以通过函数dctmtx(n)求得
for i = 0:3for j = 0:3if i == 0a = sqrt(1/4);elsea = sqrt(2/4);endA(i+1,j+1) = a*cos((j+0.5)*pi*i/4)end
end
D = A*I*A';     %DCT变换
D1 = dct2(I);   %matlab DCT函数进行DCT变换
D2 = A'*D*A;    %DCT逆变换

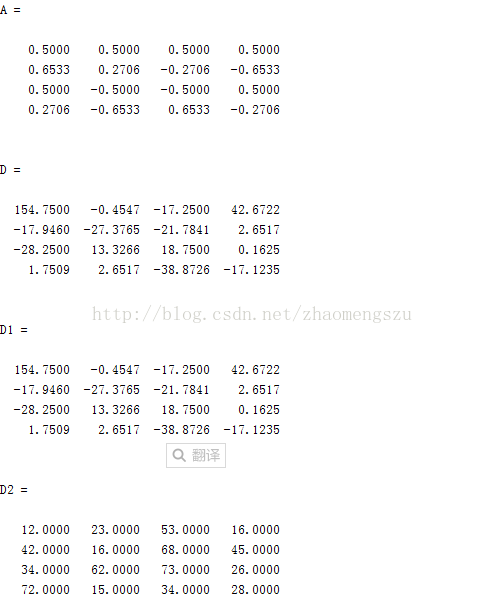
由结果可以看出，D，D1方式得到的DCT系数相同，说明矩阵形式的DCT变换公式是正确的，D2的数据与原数据I相同，实现了数据恢复。

另外通过运行函数dctmtx(4)可以发现得到的变换矩阵与A完全相同。

Matlab 函数实现

matlab实现离散余弦变换有两种方法：

一种为函数dct2( ), 使用函数dct2，该函数用一个基于FFT的算法来提高当输入较大的方阵时的计算速度。
另一种为函数dctmtx( ), 使用由dctmtx函数返回的DCT变换矩阵，这种方法较适合于较小的输入方阵（例如8×8或16×16）。
. 函数：dct2( )

实现图像的二维离散余弦变换。调用格式为：
B = dct2(A)
B = dct2(A,[M N])
B = dct2(A,M,N)
式中A表示要变换的图像，M和N是可选参数，表示填充后的图像矩阵大小，B表示变换后得到的图像矩阵。其逆变换函数为idct2( );
```
I = imread('1_1.jpg');%输入灰度图像
D = dct2(I);          %DCT变换
D1 = idct2(D);        %逆变换
subplot(1,2,1);imshow(I);
subplot(1,2,2);imshow(uint8(D1));
```
2. 函数：dctmtx( )

D = dctmtx(N)
式中D是返回N×N的DCT变换矩阵，如果矩阵A是N×N方阵，则A的DCT变换可用D×A×D’来计算。这在有时比dct2计算快，特别是对于A很大的情况。上面有提到过。

对于图像的DCT变换，这里还需用到一个函数blkproc( ),其功能为对图像分块进行DCT变换。
blkproc( )定义如下：
B = blkproc(A,[M N],Fun) ，A为输入图像，M*N为块大小，Fun为处理函数
常用的方式为：
B = blkproc(A,[8,8],’P1*x*P2’,T,T’); T为变换矩阵，P1和P2为参数，代表T*x*T’ 。

I = imread('1_1.jpg'); %输入灰度图像
I = im2double(I);
D = dctmtx(8);
C = blkproc(I,[8,8],'P1*x*P2',D,D');  %D'为D的转置
mask1=[1 1 1 1 1 0 0 0
1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];
mask2=[1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];
mask3=[1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];X = blkproc(C,[8,8],'P1.*x',mask1);  %保留15个系数
I1  = blkproc(X,[8,8],'P1*x*P2',D',D);    %重构图像
X2 = blkproc(C,[8,8],'P1.*x',mask2);  %保留10个系数
I2  = blkproc(X2,[8,8],'P1*x*P2',D',D);    %重构图像
X3 = blkproc(C,[8,8],'P1.*x',mask3);   %保留3个系数
I3  = blkproc(X3,[8,8],'P1*x*P2',D',D);    %重构图像
subplot(2,4,1);imshow(I);
subplot(2,4,2);imshow(I1);
subplot(2,4,3);imshow(I2);
subplot(2,4,4);imshow(I3);

上面代码中，通过求得图像DCT系数，利用mask等矩阵对其进行量化，保留左上角主要的系数值，对于右下角的值由于其为非常小的高频系数，量化去除后对于图像的质量影响不大，可以利用这一性质对图像进行压缩处理。

保留系数越多则图像压缩质量越好，下面比较几幅图像质量，从左到右分别为原图，mask1，mask2，mask3；