本文主要是介绍伊恩·斯图尔特《改变世界的17个方程》薛定谔方程笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
想法是等这学期学到薛定谔方程后再把整份完善下。

它告诉我们什么?
这个方程不是把物质作为粒子,而是作为波,并描述这样的波如何传播。
为什么重要?
薛定谔方程是量子力学的基础,它与广义相对论一起构成了当今最有效的物质宇宙理论。它带来了什么?在极小尺度上对描述世界的物理学进行彻底修正,其中每个粒子都具有描述可能状态的概率云的“波函数”。在这个层面上,世界本质上是不确定的。它试图将微观量子世界与宏观的经典世界联系起来,导致了至今仍有影响的哲学问题。但在实验上,量子理论非常有效,如果没有它,就没有今天的计算机芯片和激光器。
黑体辐射
这一切都从灯泡开始。这也很合情合理,因为这是从麦克斯韦出色地统一了的新兴学科——电和磁中涌现的最耀眼的应用之一。1894年,一家电气公司雇用了一位名叫马克斯·普朗克(Max Planck)的德国物理学家来设计最高效的灯泡,要发光最多,耗电最少。他看出,这个问题的关键在于物理学中的一个基本问题,这个问题是1859年由另一位德国物理学家古斯塔夫·基希霍夫(Gustav Kirchhoff)提出的。它涉及一种理论构造,称为“黑体”,它会吸收落在其上的所有电磁辐射。最大的问题是:这样的物体是如何发出辐射的?它无法把所有的辐射都存储起来,有一些肯定还要再发射出来。
特别是,发射出的辐射的强度与频率和物体的温度之间有什么关系?
热力学已经给出了一个答案,它把黑体看作一个盒子,盒壁是完美的镜子。电磁辐射在镜子之间来回反射。当系统稳定到平衡态后,盒子中的能量的频率如何分布呢?1876年,玻尔兹曼证明了“能量均分定理”:能量被均等地分配给运动的每个独立分量。这些分量就像小提琴弦上的基波一样:简正模。这个答案只有一个问题:它不可能成立。这意味着在所有频率上辐射的总功率必须是无限的。这个矛盾的结论被称为“紫外灾难”:“紫外”是因为它是高频范围的开始,而“灾难”一词确实恰如其分。没有哪个实际物体能够发射出无限的功率。
尽管普朗克意识到了这个问题,却不以为意,因为他本来也不相信能量均分定理。具有讽刺意味的是,他的工作解决了悖论,并消除了紫外灾难,但他后来才注意到这一点。他使用了对能量与频率关系的实验观察,并用数学公式拟合数据。他的公式是1900年初推导出来的,最初没有任何物理依据。但这个公式就是管用。但同年晚些时候,他试图将自己的公式与经典的热力学公式吻合起来,并认为黑体谐振子的能级不能像热力学所假设的那样连续变化。相反,这些能级必须是离散的——能级间有微小的间隙。实际上,对于任何给定频率,能量必须是该频率的整数倍,再乘上一个非常小的常数。我们现在把这个数字称为“普朗克常量”,用h表示。第一次这样的测量是由罗伯特·密立根(Robert Millikan)使用后文描述的光电效应进行的。微小的能量包现在被称为“quanta”(量子quantum的复数),来自拉丁语quantus(多少)。
普朗克常量可能确实很小,但如果给定频率的能级集合是离散的,则总能量就是有限的。所以紫外灾难是一个连续模型未能反映大自然的标志。这意味着,在极小尺度上,大自然必须是离散的。最初普朗克并没有想到这一点,他认为自己的离散能级是一个数学技巧,可以得到一个合理的公式。事实上,玻尔兹曼在1877年也曾有过类似的想法,但并没有进一步深入。但当爱因斯坦丰沃的想象力结出硕果时,一切都变了,物理学进入了一个新的王国。1905年,也就是他提出狭义相对论的同一年,他研究了光电效应,即让光撞击合适的金属,使其发射电子。三年前,菲利普·莱纳德(Phillipe Lenard)注意到,光线频率更高时,电子的能量也更高。但是麦克斯韦充分证实了光的波动理论,暗示电子的能量应该取决于光的强度,而不是它的频率。爱因斯坦意识到普朗克的量子将解释这种差异。他认为,光不是波,而是由微小的粒子组成的,现在我们把它称为“光子”。给定频率的单个光子的能量应该是频率乘以普朗克常量——就像普朗克的一个量子一样。光子就是光的量子。
爱因斯坦的光电效应理论有一个明显的问题:它假设光是粒子。但是有大量证据表明光是波。另外,光电效应与光是波这一点不相容。那么光是波吗?是粒子吗?是。它两者都是——或者说,分别在某些方面有所表现。在一些实验中,光看起来像是波。在其他情况下,它表现得像是粒子。当物理学家开始理解极小尺度的宇宙时,他们认为光不是唯一具有这种奇怪的双重性质的东西,有时是粒子,有时是波。所有的物质都是如此。他们称之为“波粒二象性”。第一个理解这种双重性质的人是路易斯–维克多·德布罗意(Louis-Victor de Broglie),当时是1924年。他用动量而不是能量来改写普朗克定律,并且暗示粒子性的动量和波动性的频率应该是相关的:把二者乘起来就会得到普朗克常量。三年后,他的理论被证明正确,至少对于电子而言如此。一方面,电子是粒子,我们可以观察到这方面的行为;另一方面,它们像波一样发生衍射。1988年,钠原子也被发现有波动性。
批注:其实德布罗意公式也挺美的。
薛定谔方程
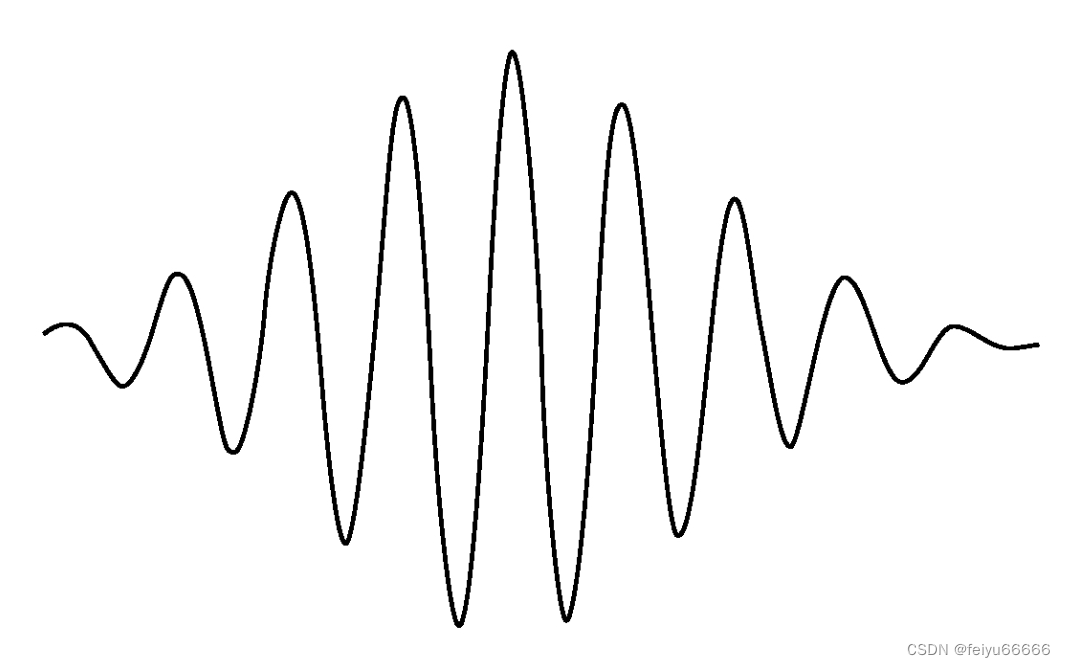
物质既不是粒子(particle)也不是波(wave),而是两者兼而有之——波动粒子(wavicle)。人们为物质的双重性质设计了几种多少有些直观的图像。在一张图中,粒子是局部的波群,称为“波包”,如图所示。
整个波包可以表现得像一个粒子,但一些实验可以探测其内部的波状结构。人们的注意力从创造波动粒子的图像转移到了解它们的行为方式。这个任务很快达成了目标,量子理论的核心方程出现了。这个方程被冠上了埃尔温·薛定谔的名字。1927年,在其他几位物理学家,特别是维尔纳·海森堡(Werner Heisenberg)的工作基础上,他写下了任意量子波函数的微分方程。方程看起来像这样:
这里的
描述了波的形式,t是时间(因此对
取
就得到了它对时间的变化率),
是一个称为哈密顿算符的表达式,而ħ是
,其中h是普朗克常量。那么i呢?这是方程中最奇怪的特征。它是-1的平方根(见第5章)。薛定谔方程适用于定义在复数上的波,而不仅仅是我们熟知的波动方程那样的实数。
哪里的波呢?经典波动方程(见第8章)定义了空间中的波,其解是空间和时间的数值函数。薛定谔方程也是如此,但现在波函数[插图]取复数值,而不仅仅是实数值。这有点儿像是一个高度为[插图]的海浪。从很多方面来讲,[插图]的出现是量子力学最神秘、最深刻的特征。以前[插图]曾经出现在方程的解以及求得这些解的方法中,但在这里它是方程的一部分,是物理定律中的一个明确特征。
对于这一点,有一种解释是,量子波是一对相关联的真实的波,就像复数海浪其实是两个波浪,一个高度是2,另一个高度是3,两个高度的方向彼此成直角。但它并不那么简单,因为这两个波浪没有固定的形状。随着时间的推移,它们在一系列形状之间循环,各个形状之间存在着神秘的联系。它有点儿像光波的电和磁分量,但现在电可以并且确实“旋转”成了磁,反之亦然。两个波是一个形状的两个面,它在复平面中围绕单位圆稳定旋转。这种旋转的形状的实部和虚部都以非常特殊的方式变化:它们以正弦变化的量组合起来。在数学上,这引出了量子波函数具有某种特殊类型的相位的想法。这个相位的物理解释与经典波动方程中相位的作用相似但不同。
批注:一脸懵。
还记得傅里叶解决热方程和波动方程的技巧吗?一些特解,比如傅里叶的正弦和余弦,具有特别令人高兴的数学特性。所有其他的解,无论多么复杂,都是这些简正模的叠加。我们可以使用类似的思想来解薛定谔方程,但现在基本的模式要比正弦和余弦更复杂。它们被称为本征函数,我们可以把它们与所有其他的解区分开来。
本征函数不是一般性的空间和时间的函数,而是仅取决于空间的函数,乘以仅取决于时间的函数。用行话来说,空间和时间变量是可分离的。本征函数取决于哈密顿算符,这是对此类物理系统的数学描述。不同的系统(势阱中的电子、一对碰撞的光子、随便什么东西)具有不同的哈密顿算符,因此具有不同的本征函数。
为简单起见,考虑一个经典波动方程的驻波——一根末端被固定住的振动的小提琴弦。在所有时刻,弦的形状几乎相同,但振幅有波动:乘以一个随时间正弦变化的因子。量子波函数的复杂相位与此类似,但更难画出来。对于任何一个单独的本征函数,量子相位变化的效果就只是时间坐标的变化。对于几个本征函数的叠加,我们可以把波函数分解为这些分量,将每个分量分解为纯空间部分乘以纯时间部分;围绕复平面中的单位圆,以适当的速度旋转时间部分;再把这些分量重新拼在一起。每个单独的本征函数具有复振幅,并且振幅以其自己的特定频率波动。
这可能听起来很复杂,但如果你没有把波函数分解为本征函数,那就完全是一团糟了。现在至少你还有机会。尽管存在这些复杂性,但量子力学只是经典波动方程的一个花哨的版本,它会得出两个波,而不是一个波——但还有一件怪事让人费解。经典波是可以观察的,看看它们是什么形状,哪怕它是几种傅里叶模式的叠加。但在量子力学中,你永远无法观察到整个波函数。你在任何特定时刻所能够观察到的只是单个分量本征函数。粗略地说,如果你尝试同时测量其中两个分量,其中一个分量的测量过程会干扰另一个分量。
这立刻引发了一个困难的哲学问题。如果无法观察整个波函数,它实际存在吗?它是一个真正的物理对象,还只是一个方便的数学构想?难以观察的数量是否具有科学意义?薛定谔的那只著名的猫正是在这里出现的。它的产生源于量子测量的一种标准解释,称为哥本哈根诠释。
哥本哈根诠释与薛定谔的猫
想象一下处于某种叠加状态的量子系统。例如,一个电子,其状态是自旋向上和自旋向下的混合,这两种自旋是由本征函数定义的纯态(自旋向上和自旋向下具体是什么意思并不重要)。但是,当你观察状态时,你要么观察到自旋向上,要么观察到自旋向下。你无法观察到叠加。此外,一旦你观察到其中一个(比如说自旋向上),它就会成为电子的实际状态。你的测量似乎以某种方式迫使叠加变成了特定的分量本征函数。这种哥本哈根诠释基本上就是这样理解的:你的测量过程将原始波函数坍缩成了单个纯本征函数。
如果观察大量的电子,你会看到有时自旋向上,有时自旋向下。你可以推断出电子处于其中一种状态的概率。因此波函数本身可以被解释为一种概率云。它没有显示电子的实际状态:它显示了当你测量它时,你得到一个特定的结果的可能性。但这使它成为一种统计模式,而不是真实的存在。它不能证明波函数是真实的,就像凯特勒对人体高度的测量不能证明正在发育的胚胎具有某种钟形曲线。
哥本哈根诠释简单明了,它反映了实验中发生的事情,而且没有对观察量子系统时会发生什么做出详细的假设。由于这些原因,大多数工作物理学家非常乐意使用它。但是在这个理论仍然被反复讨论的早期,有些人不同意,而有些人至今依然不同意。其中的一位反对者就是薛定谔本人。
批注:简单明了???你是不是对简单明了有什么误解?
1935年,薛定谔为哥本哈根诠释心神不宁。他可以看到它在实用层面上对电子和光子等量子系统是有效的。尽管他周围的世界内部深处只是一团沸腾的量子粒子,看起来却与此不同。为了找到一种让这个区别尽可能明显的方法,薛定谔提出了一个思想实验,让量子粒子对猫产生出人意料的明显效果。
想象一个盒子,它在关闭时不受任何量子相互作用的影响。在盒子里放一个放射性原子、一个辐射探测器、一瓶毒药和一只活猫。现在把盒子关上并等待。在某个时刻,放射性原子会衰变并发射出一个辐射粒子。探测器会探测到它,此时就会触发机关,打碎瓶子并释放毒药,毒药会杀死猫。
在量子力学中,放射性原子的衰变是随机事件。从外面看,任何观察者都无法判断原子是否已经衰变。如果它衰变了,猫就死了;如果没有衰变,猫就还活着。根据哥本哈根诠释,它是两个量子态的叠加——要么衰变,要么没有衰变,直到有人观察到了原子。探测器、瓶子和猫的状态也是如此。因此,猫处于两种状态的叠加:死去和活着。
由于盒子不受任何量子相互作用的影响,因此知道原子是否已经衰变并杀死猫的唯一方法就是打开盒子。哥本哈根诠释告诉我们,在我们这样做的瞬间,波函数就发生坍缩,猫突然变为纯态:死去或活着。但是,盒子内部和外部世界并没有什么不同,而我们从未观察到生存/死亡状态叠加的猫。因此,在我们打开盒子并观察其内部之前,里面的猫要么死了,要么活着。
薛定谔认为这个思想实验是对哥本哈根诠释的批评。微观量子系统遵循叠加原理,可以以混合态存在;宏观系统则不能。通过将微观系统(原子)与宏观系统(猫)联系起来,薛定谔指出了他认为哥本哈根诠释存在的一个缺陷:当它应用于猫时就是无稽之谈。他一定会对大多数物理学家的回应感到震惊:“是的,埃尔温,你完全正确。直到有人打开盒子,猫真的是同时死去和活着的。”特别是当他发现,哪怕打开盒子,看到一只活着或是死去的猫,他也无法决定谁是对的。他可能会推断猫在打开盒子之前已经处于那种状态,但他无法确定。可观察到的结果与哥本哈根诠释一致。
当然,我们还可以这样做:在盒子里放上一部胶片摄像机,并拍摄实际发生了什么。这样就有定论了。“啊,不,”物理学家回答道,“只有打开盒子后才能看到摄像机拍摄的内容。在此之前,这部电影处于叠加状态:一部猫活着的电影,和一部猫死去的电影。”
哥本哈根诠释解放了物理学家,让他们可以计算并搞清楚量子力学预测的内容,而无须面对这个困难的(如果不是不可能解决的)问题——经典世界如何在量子基础上构建,一个在量子尺度上复杂得难以想象的宏观设备如何可以测量量子态。由于哥本哈根诠释行得通,他们并不是真正对哲学问题感兴趣。因此,一代代物理学家所学的都是,薛定谔发明了他的猫来证明量子叠加也可以扩展到宏观世界——与薛定谔原本试图告诉他们的完全相反。
批注:这就像水课签到一样。直到老师点我名,,,
物质在电子和原子的层次上表现奇怪并不太出人意料。我们最初可能会因为不熟悉而抗拒这个想法,但如果一个电子真的是一小团波,而不是一小块实物,我们还是可以学会接受它。如果这意味着电子的状态本身有点儿奇怪,不仅绕轴向上或向下旋转,而是两者兼有,我们也可以忍受。如果测量设备的局限性意味着我们永远无法捕捉到电子的这种表现(我们所做的任何测量必然都只能是一些纯态,向上或向下),那也就这样吧。如果这同样适用于放射性原子,状态要么是“已衰变”,要么是“未衰变”,因为组成它的粒子具有类似于电子那样难以捉摸的状态,我们甚至可以接受整个原子本身就是那些状态的叠加,直到我们进行测量。但猫就是猫,对于这只动物同时活着和死去,只有当我们打开盒子时才奇迹般地坍缩成一个或另一个状态的情景,似乎就需要努力想象了。如果量子的现实需要一个生死状态叠加的猫,那它为什么如此害羞,以至于不让我们观察到这个状态呢?
在量子理论的形式中,(直到最近)有充分的理由要求任何测量,即任何“可观察量”,都是本征函数。甚至还有更坚实的理由来相信为什么量子系统的状态应该是一个波,并遵循薛定谔方程。怎么才能从一个状态变到另一个状态呢?哥本哈根诠释声称,测量过程以某种方式(不要问是什么方式)将复杂的叠加波函数坍缩成单个分量本征函数。既然有了这种形式的说法,你作为物理学家的任务就是继续做测量和计算本征函数之类的事,而不要再问令人尴尬的问题。如果成功是用答案是不是和实验一致来衡量的话,那它的效果好得惊人。如果薛定谔方程允许波函数有这样的行为,那就万事大吉了,但它没有。在《隐藏的现实》(The Hidden Reality)一书中,布莱恩·格林(Brian Greene)这样说道:“即使是礼貌的探究也会发现让人不安的特征…… 波的瞬间坍缩…… 不可能从薛定谔的数学中产生出来。”相反,哥本哈根诠释是理论的一种实用主义附属品,一种处理测量的方法,无须理解或面对它到底是怎么回事。
为什么宇宙看起来是经典的?
这一切都很好,但这并不是薛定谔想要指出的。他引入了一只猫,而不是一个电子或原子,因为这把他心目中的主要问题放在了最为醒目的地方。猫属于我们生活的宏观世界,其中物质的行为并不像量子力学所要求的那样。我们没有看到叠加的猫。薛定谔问为什么我们熟悉的“经典”宇宙并不与底层的量子现实相似。如果构造世界的一切都可以存在于叠加状态,那为什么宇宙看起来是经典的?许多物理学家进行了精彩的实验,表明电子和原子的行为确实符合量子和哥本哈根的推断。但这忽略了一点:你必须用猫做实验。理论家们想知道这只猫是否可以观察它自己的状态,或者其他人是否可以偷偷打开盒子并记下里面的情况。按照薛定谔的逻辑,他们得出的结论是,如果猫观察到自己的状态,那么盒子里就有一只通过观察自己而自杀的死猫,再叠加上一只观察到自己活着的活猫,直到合法观察者(物理学家)打开盒子。然后这一整套东西就会坍缩到某个状态。同样,这位朋友也成了两个朋友的叠加:其中一个人看到了一只死猫,而另一个人看到了一只活猫,直到物理学家打开盒子,导致朋友的状态坍缩。这套逻辑可以一直持续下去,直到整个宇宙的状态是一个有死猫的宇宙和一个有活猫的宇宙的叠加,然后当物理学家打开盒子时,宇宙的状态就会发生坍缩。
这有点儿令人尴尬。物理学家可以继续他们的工作而不去把它搞清楚,他们甚至可以否认有事情需要搞清楚,但还是缺了点儿什么。例如,如果阿佩罗贝特尼三号行星上的外星物理学家打开盒子,会发生什么?我们是否会突然发现,我们其实已经在一次小行星撞击地球后灭亡了,从那时起一直生活在借来的时间里?测量过程并不是哥本哈根诠释所设想的那种漂亮、整洁的数学运算。当被要求描述这个设备如何做出决定时,哥本哈根诠释会回答:“它就是做了。”波函数坍缩到单个本征函数的图像描述了测量过程的输入和输出,但没有描述如何从一个状态变成另一个状态。但是当你真正进行测量时,你并不能挥一下魔杖就让波函数不服从薛定谔方程而坍缩。相反,从量子的角度来看,你做了一件非常复杂的事情,要对它进行逼真的建模显然是毫无希望的。例如,为了测量电子的自旋,你让它与一个合适的装置相互作用,这个装置有一个指针,可以移动到“向上”或“向下”的位置。或是通过数字显示,或是把信号发送给计算机…… 此设备得出一个状态,而且只能得出一个状态。你不会看到指针处于上下叠加状态。
费曼的解释
我们还是对我们的经典世界如何由背后的量子世界产生有了一些了解。我先来讲一个简单的版本:光照射镜子。经典的答案——斯涅尔定律指出,反射光会以与入射光相同的角度反射出来。在关于量子电动力学的《QED:光和物质的奇妙理论》一书中,物理学家理查德·费曼(Richard Feynman)解释说,这不是量子世界中发生的事情。光线实际上是光子流,每个光子都可以随便反弹到什么地方。但是,如果你把光子能做的所有事情都叠加起来,就得到了斯涅尔定律。绝大部分光子以非常接近入射角的角度反弹回来。费曼甚至设法不使用任何复杂的数学就说明了为什么,但在这个计算背后是一个通用的数学思想:固定相原理。如果将光学系统的所有量子态叠加在一起,就会得到经典的结果,即光线遵循以所花时间衡量的最短路径。你甚至可以加上一些花哨的东西,给光路点缀上一些经典的波动光学衍射条纹。
这个例子非常明确地表明,所有可能世界的叠加(在这个光学框架中)得出了经典世界。最重要的特征不是光线的详细几何,而是它在经典层面上仅产生一个世界。在单个光子的量子细节中,你可以观察到叠加、本征函数等所有东西。但是在人类的尺度上,那些都抵消掉了——好吧,叠加在一起——得到一个干净、经典的世界。
解释的另一部分称为退相干。我们见过,量子波具有相位和振幅。这是一个非常滑稽的相位,它是一个复数,但无论如何仍然是相位。这个相位对于任何叠加都是至关重要的。如果你取两个叠加的状态,改变其中的一个相位,并将它们重新加在一起,得到的结果就面目全非了。如果你对很多分量做同样的事情,重新组装的波几乎可以是任何东西。丢失相位信息会破坏任何类似于薛定谔的猫的叠加。你不只是丢失了它是活着还是死了的信息,你甚至看不出它是一只猫。当量子波不再具有良好的相位关系时,就会发生退相干——它们开始表现得更像经典物理学,而叠加则失去了所有意义。导致它们退相干的原因是与周围粒子的相互作用。想必仪器就是靠这个测量电子自旋并获得特定的唯一结果的。
这两种方法都得出了相同的结论:如果你对一个非常复杂的量子系统进行人类尺度下的观测,那么你就会观察到经典物理学。特殊的实验方法、特殊的装置,可能会保留一些量子效应,让它们在我们舒适的经典存在中凸显出来,但随着我们转向更大的行为尺度,通用量子系统很快就不再体现量子性。
这是解决可怜的猫的命运的一种方法。只有当盒子完全不受量子退相干的影响时,实验才能产生叠加的猫,然而这样的盒子不存在。你拿什么造这个盒子呢?
埃弗利特的解释
但还有另一种方式,一种相反的极端。我在前面说过:“这套逻辑可以一直进行下去,直到整个宇宙的状态是一个叠加。”1957年,小休·埃弗里特(Hugh Everett Jr.)指出,从某种意义上说,你必须这样做。为一个系统提供精确量子模型的唯一方法是考虑其波函数。每个人都很乐意这样做,不管系统是电子、原子,还是猫(比较有争议)。埃弗里特把这个系统变成了整个宇宙。
他认为,如果那是你想要建模的东西,那你别无选择。只有宇宙才能真正被孤立。一切都与其他一切相互作用。他发现如果你走到了这一步骤,那么猫的问题,以及量子和经典现实之间的矛盾关系就很容易解决了。宇宙的量子波函数不是纯粹的本征模,而是所有可能的本征模的叠加。虽然我们无法计算这些东西(连猫都算不出来,宇宙还要更复杂一点),但我们可以推理。事实上,在量子力学意义上,我们把宇宙表达为宇宙可以做的所有可能事物的组合。
其结果是,猫的波函数并不一定要坍缩并得出单一的经典观测。它可以保持完全不变,不违反薛定谔方程。相反,有两个共存的宇宙。其中一个宇宙中的猫死了;在另一个宇宙中,它则没有死。当你打开盒子时,相应地也会有两个你和两个盒子。其中一个属于有死猫的宇宙的波函数,另一个属于有活猫的宇宙的另一个波函数。我们拥有的不是以某种方式从量子可能性的叠加中产生的一个独特的经典世界,而是许许多多的经典世界,每一个都对应于一种量子可能性。
埃弗里特的原始版本(他称之为“相对态构造”)在20世纪70年代引起了人们的关注,因为布赖斯·德威特(Bryce DeWitt)给了它一个更吸引人的名字:量子力学的多世界诠释。它常常从历史的角度被戏剧化。例如,存在一个阿道夫·希特勒赢得了第二次世界大战的宇宙,以及另一个他没有赢的宇宙。我正在写这本书的宇宙是后者,但在量子王国的另一个地方,伊恩·斯图尔特正在写一本与之非常类似的书,却是以德语写的,这提醒着他的读者,他们身处希特勒获胜的宇宙中。在数学上,埃弗里特的解释可以被视为传统量子力学的逻辑等价物,并且(在更局限的解释中)带来了解决物理问题的有效方法。因此,他的形式将能够经受传统量子力学所经受的任何实验检验。那么,这意味着这些平行宇宙,也就是美国人所说的“或然世界”(alternate world),真的存在吗?在希特勒获胜的世界里,有另一个我在计算机键盘上愉快地打字?还是说,这只是一个方便的数学构想?
有一个明显的问题:我们如何能够确定,在一个由希特勒所幻想“千年帝国”统治的世界中,也会存在我所使用的这种计算机?显然,肯定有比两个多得多的宇宙,其中的事件必须遵循合理的经典模式。也许斯图尔特–2不存在,但希特勒–2确实存在。对平行宇宙的形成和演化的常见描述,会谈到它们在有量子态的选择时“分裂”。格林指出这个图景是错误的:没有什么分裂。宇宙的波函数已经并且将永远是分裂的。它的分量本征函数就在那里:当选择其中一个时,我们会想象一个分裂,但埃弗里特的解释的关键就在于,波函数中的任何东西都没有实际变化。
虽然有这样的问题,但数量惊人的量子物理学家接受了多世界诠释。薛定谔的猫既活着又死了。我们的一个版本生活在一个那样的宇宙中,而其他版本则没有。这就是数学所说的。它不是解释,而是一种方便的安排计算的方式。它和你我一样真实。它就是你我。
这种说法没有说服我。不过,困扰我的并不是叠加。我并不觉得存在一个平行世界是不可想象的,或者说是不可能的。但我确实激烈反对这样一种观点,即你可以根据人类尺度的历史叙事来分离量子波函数。数学分离发生在组成粒子的量子态水平上。大多数粒子状态的组合对人类叙事没有任何意义。死猫的一个简单替代品并不是活猫。它是一只有一个电子处于不同状态的死猫。复杂的替代品则要比一只活猫多得多。它们包括一只突然毫无理由爆炸的猫、一只变成花瓶的猫、一只被选为美国总统的猫,还有一只哪怕放射性原子释放了毒药依然活下来的猫。那些替代猫用作说辞很有用,但没有代表性。大多数替代品不是猫;事实上,它们难以用经典术语来形容。如果是这样的话,大多数斯图尔特的替代品根本看不出人形——事实上什么形也看不出来——而且几乎所有这些东西都存在于一个在人类看来根本没有任何意义的世界里。所以说,另一个版本的我,碰巧生活在另一个有人类叙事意义中的世界里的可能性微乎其微。
宇宙很可能是替代状态复杂得难以置信的叠加。如果你认为量子力学基本上是正确的,那就必须如此。1983年,物理学家斯蒂芬·霍金说,在这个意义上,多世界诠释“显然是正确的”。但这并不意味着存在一只猫活着或死了,以及希特勒获胜或失败的宇宙的叠加。我们没有理由认为数学分量可以分成适合于创造人类叙事的集合。霍金驳斥了对多世界形式的叙述性诠释,并说:“说白了,这一切都是为了计算条件概率——换句话说,B发生时A发生的概率。我认为多世界诠释就是这么回事。有些人给它添上了好多关于波函数分裂成不同部分的神秘主义色彩。但你计算的无非是条件概率而已。”
批注:多世界诠释。。。
两个希特勒的故事值得与费曼的光线的故事比较一下。与之前故事风格不同的是,费曼会告诉我们,有一个经典世界,光线照到镜子上会以和入射角相同的角反射;有另一个经典世界,反射角会差一度;还有一个世界会差两度,等等。但他没有。他告诉我们,有一个经典世界从量子的各种可能性的叠加中产生。量子层面上可能存在无数个平行世界,但这些世界并不以任何有意义的方式对应于可以在经典层面上描述的平行世界。斯涅尔定律适用于任何经典世界。如果不是,那个世界就不可能是经典的。就像费曼对光线的解释那样,当你把所有的量子可能性都叠加起来时,就会出现这一个经典世界。只有一个这样的叠加,所以只有一个经典宇宙——我们的宇宙。
量子力学的应用
量子力学并不仅限于实验室。整个现代电子都依赖它。半导体技术是所有集成电路的基础,而硅芯片是符合量子力学的。如果没有量子的物理学,你根本不敢想这样的设备可以工作。计算机、手机、CD播放器、游戏机、汽车、冰箱、烤箱,几乎所有现代家用电器都有存储芯片,以存储指令来让这些设备满足我们的需求。许多芯片包含更复杂的电路,例如微处理器就是把整个计算机置于一个芯片上。大多数存储芯片从第一个真正的半导体器件——晶体管演变而来。
在20世纪30年代,美国物理学家尤金·维格纳(Eugene Wigner)和弗雷德里克·塞茨(Frederick Seitz)分析了电子如何通过晶体运动,这是一个需要量子力学来解决的问题。他们发现了半导体的一些基本特征。有些材料是电导体:电子可以很容易地流过它们。金属是良好的导体,我们日常普遍使用的是铜线。绝缘体不允许电子流动,因此可以阻止电流:电线的塑料外皮就是绝缘体,可以防止我们被电视的电源线电到。半导体两者兼而有之,取决于具体的情况。硅是最著名的半导体,目前使用得也最广泛,但其他几种元素,如锑、砷、硼、碳、锗和硒也是半导体。因为半导体可以从一种状态切换到另一种状态,所以它们可以用来控制电流,而这就是所有电子电路的基础。
维格纳和塞茨发现,半导体的特性取决于其内部电子的能级,而这些能级可以通过“掺杂”,即给本征半导体材料添加少量特定杂质来控制。杂质半导体有两种重要的类型:n型半导体,以电子流的形式传输电流;p型半导体,其中电流以与电子流相反的方向流动,由“空穴”(电子数量少于正常值的地方)传输。1947年,贝尔实验室的约翰·巴丁(John Bardeen)和沃尔特·布拉顿(Walter Brattain)发现锗晶体可以用作放大器。如果向其馈入电流,则输出电流更高。固态物理部门的负责人威廉·肖克利(William Shockley)意识到了这有多么重要,启动了一个研究半导体的项目。晶体管(transistor,“transfer resistor”[传输电阻]的缩写)就在这里诞生了。有一些专利比它更早,但没有能够工作的器件或发表的论文。自从这个最初的突破以来,人们已经发明了许多类型的晶体管。一种晶体管器件是JFET(结型场效应晶体管,图14.2)。美国德州仪器公司于1954年制造出了第一个硅晶体管。同年,美国军方建造了一台基于晶体管的计算机TRIDAC。它的体积是3立方英尺,消耗的功率相当于一个灯泡。美国有一个庞大的军事计划来开发真空管电子设备的替代品,因为这种设备对军事用途而言太笨重、太易碎,也太不可靠了。这台计算机就是计划中的早期一步。
批注:原来原理是量子力学,当时讲的时候就知道具体是怎么回事而已。。。
量子力学的另一个普遍应用是激光。这种装置发射的是强相干光束——所有光波彼此同相。装置中有一个光学腔,腔两端各有一面镜子,腔中充满了可以对特定波长的光做出反应并产生更多相同波长的光的物质——光放大器。泵入能量以启动这个过程,让光线沿着腔体来回反复并一直放大,当它达到足够高的强度后释放出来。增益介质可以是流体、气体、晶体或半导体。不同的材料用于不同的波长。放大过程取决于原子的量子力学。原子中的电子可以有不同的能级,并且可以通过吸收或发射光子来在能级之间跃迁。
激光(laser)一词意为“通过受激辐射的光放大”。第一台激光器被发明出来时,很多人嘲笑它是拿着答案找问题。这些人真的缺乏想象力:一旦有解决方案,一系列合适的问题就会迅速涌现出来。产生相干光束是一项基础技术,它必然有用,就像经过改进的锤子也会自动找到许多用途一样。在发明通用技术时,你不必考虑特定的应用。今天,激光器的用途已经不胜枚举。它有比较平凡的用途,比如讲课用的激光笔,或是家居修理用激光束。CD播放机、DVD播放机和蓝光都使用激光从光盘上的小凹坑或标记中读取信息。测绘员使用激光测量距离和角度。天文学家使用激光测量从地球到月球的距离。外科医生使用激光切割精细组织。用激光治疗眼睛也十分普遍,它用于修复脱落的视网膜,或是重塑角膜表面以矫正视力,病人就不用戴框架眼镜或隐形眼镜了。“星球大战”反导弹系统本想使用强大的激光击落敌人的导弹,虽然它从未建成,但有些激光器建成了。人们目前正在研究激光的军事用途,类似于烂俗科幻小说中的光枪。甚至有可能让飞行器乘着强大的激光束飞向太空。
批注:激光。
量子力学的新用途几乎每个星期都会出现。最近出现了一个“量子点”,即微小的半导体片,其电子特性(包括它们发出的光)会根据其大小和形状而变化。因此我们可以定制它来获得许多好的特性。它们已经有很多应用,比如生物成像,可以替代传统的(通常是有毒的)染料。它们的性能更好,发出的光更亮。一些工程师和物理学家正在研究量子计算机的基本组件。在这样的设备中,0和1的二进制状态可以以任何组合叠加,相当于允许计算同时取两个值。这将允许它并行执行许多不同的计算,从而极大地提升速度。理论算法已经被设计出来,用于执行诸如将数字分解为质因数的任务。当数字超过一百位左右时,传统的计算机会遇到麻烦,但量子计算机应该能够轻松地分解更大的数字。量子计算的主要障碍是退相干,它会破坏叠加态。薛定谔的猫正在为其遭受的不人道待遇展开报复。
这篇关于伊恩·斯图尔特《改变世界的17个方程》薛定谔方程笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!