本文主要是介绍【软件构造】实验笔记(二)Lab2-Abstract Data Type and Object-Oriented Programming,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、前言
因为有一些事情耽误了,这次实验的笔记写的比较晚。而本次实验比上次就要复杂了很多,主要考察抽象数据类型和面相对象的编程方法。总的来说算法难度不是特别大,但是任务比较多,实现比较复杂,而且题目要求部分为英文(来自国外大学网站),所以也比较需要时间。
二、实验要求
1、Poetic Walks
请阅读 http://web.mit.edu/6.031/www/sp17/psets/ps2/ ,遵循该页面内的要求完 成编程任务。
2、Re-implement the Social Network in Lab1
回顾 Lab1 实验手册中的 3.2 节 Social Network,你针对所提供的客户端代码 实现了FriendshipGraph 类和 Person 类。 在本次实验中,请基于你在 3.1 节 Poetic Walks 中定义的 Graph及其两种实现,重新实现 Lab1 中 3.3 节的 FriendshipGraph 类。 注 1:可以忽略你在 Lab1 中实现的代码,无需其基础上实现本次作业; 注 2:在本节 FriendshipGraph 中,图中的节点仍需为 Person 类型。故你 的新 FriendshipGraph 类要利用 3.1 节已经实现的 ConcreteEdgesGraph 或 ConcreteVerticesGraph,L 替换为 Person。根据 Lab1 的要求, FriendshipGraph 中应提供 addVertex()、addEdge()和 getDistance()三 个方法: 针对 addVertex() 和 addEdge() ,你需要尽可能复用 ConcreteEdgesGraph或 ConcreteVerticesGraph中已经实现的 add() 和 set()方法,而不是从 0 开始写代码实现或者把你的 Lab1 相关代码直接复制 过来;针对 getDistance()方法,请基于你所选定的 ConcreteEdgesGraph 或 ConcreteVerticesGraph的 rep 来实现,而不能修改其 rep。 注 3:不变动 Lab1 的 3.3 节给出的客户端代码(例如 main()中的代码),即同样的客户端代码仍可运行。重新执行你在 Lab1 里所写的 JUnit 测试用例,测试你在本实验里新实现的 FriendshipGraph 类仍然表现正常。
3、Playing Chess
前面 3.1 和 3.2 节是在已经给定 ADT 设计的基础上进行具体实现和测试。本 节要求你从 0 开始设计一套 ADT,支持实现特定的功能需求。
棋类游戏由一个棋盘、一组棋子组成,双方交替在棋盘上走棋。本实验仅考虑在正方形棋盘上进行的棋类游戏,包括国际象棋和围棋。一个尺寸为 nn 的棋盘:其中 n 表示每一行/每一列的格子数。例如:围棋盘由 1818 个格子构成,国际象棋盘由 88 个格子构成。棋盘上共有 nn 个格 子和(n+1)*(n+1)个交叉点。 一组棋子:每个棋子属于一个特定的种类,不同的棋类游戏中包含的棋子种 类不同,例如:围棋/五子棋中仅包含黑子和白子;国际象棋中包含 king、queen、 rock、bishop 等类型,且双方棋手拥有同样的棋子(用颜色区分)。在一盘棋局中,不同种类的棋子的数量不同,例如国际象棋中每方有 2 个 rock、 2 个 bishop;围棋中的黑子和白子数量无限多。在游戏进行过程中,需要区分棋子是属于游戏中的哪一方玩家。
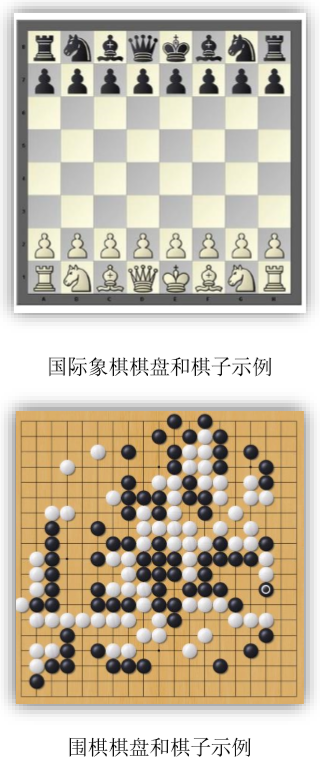
下棋过程中,棋手的动作包括:
⚫ 将一个棋子从棋盘外放到棋盘上的某个合法位置(围棋、五子棋等)
⚫ 将一个棋子从棋盘上的一个合法位置移动到另一个合法位置(中国象棋、 国际象棋等)
⚫ 将对方的一个或多个棋子从棋盘上移走
这里的合法位置是指:格子内(例如国际象棋、五子棋)或交叉点(例如围 棋、中国象棋),均使用坐标(x, y)表示。如果是格子内的位置,x 和 y 分别表 示该格子的横纵坐标,x 和 y 的取值范围是[0,n-1];如果是交叉点的位置,那 么将棋盘的第(0,0)个格子的左下角作为坐标系的原点,那么 x 和 y 表示棋盘上 第(x,y)个格子的左下角的点,且 x 和 y 的取值范围是[0,n]。如下图所示,红 色标签表示其左下方的交叉点的坐标,蓝色坐标表示其所处的格子的坐标。两个 玩家分别位于棋盘的下方和上方。
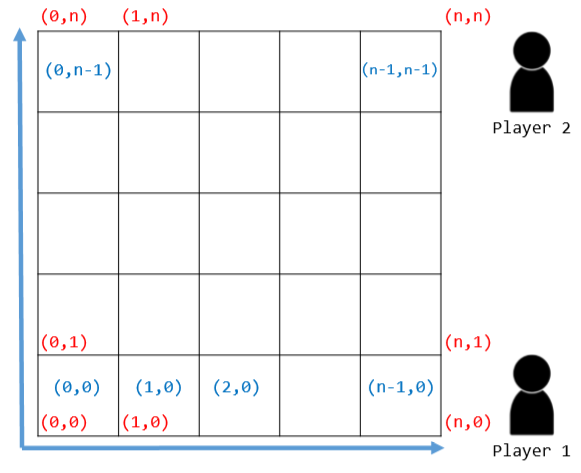
使用 Java OOP 实现一个简单的棋类模拟软件。为“一盘棋类游戏”、“玩 家”、“棋盘”、“棋子”、“棋盘上的位置”、“下棋动作”设计 ADT(类或 接口),命名分别为 Game、Player、Board、Piece、Position、Action。如 果针对不同的棋类游戏需要从这些类派生子类或者实现接口,请自行进行设计。
你可自由为所有的类/接口设计 rep 和方法,能够支持完成以下功能:
(1) 输入是游戏的类型(围棋或国际象棋),创建一个符合该棋类游戏的一个 Board 对象、一组 Piece 对象。棋盘大小、棋子种类、棋子数量无需外部参数输入,你的方法可读取外部配置文件或以静态常量写入代码,需要 符合围棋和国际象棋的真实规则;
(2) 给定两个名字,初始化两个 Player 对象;将各 Piece 对象的所有权分 配给两个 Player 对象(在围棋中,所有白子都属于 player1,所有黑子 都属于 player2;在国际象棋中,双方的棋子种类和数量都是完全一样 的,只有颜色不同);如果是国际象棋,需要将所有 Piece 对象放置到 棋盘上的初始位置(见上页图,各棋子的初始位置必须要符合国际象棋规 则);如果是围棋,则所有棋子不需放到棋盘上(上页图表示的是下棋过 程中的某个特定时刻的状态,围棋棋盘的初始状态是棋盘上无任何棋子)。
(3) 给定“棋手、一颗棋子、指定位置的横坐标、指定位置的纵坐标”作为输 入参数,将该棋手的该颗棋子放置在棋盘上(考虑游戏的类型,不同的棋 类游戏中的位置含义不同)。需考虑异常情况,例如:该棋子并非属于该 棋手、指定的位置超出棋盘的范围、指定位置已有棋子、所指定的棋子已 经在棋盘上等。——注:无需考虑实际的落子规则,但你可以扩展该 spec 让你的该操作能具备遵循国际象棋/围棋的真实落子规则的能力。
(4) 移动棋子(针对国际象棋):给定“棋手、初始位置和目的位置的横纵坐 标”,将 处于初始位置的棋子移动到目的位置。需要考虑处理各种异常情 况,例如:指定的位置超出棋盘的范围、目的地已有其他棋子、初始位置 尚无可移动的棋子、两个位置相同、初始位置的棋子并非该棋手所有等。 ——注:无需考虑实际的走棋规则,但你可以扩展该 spec 让你的该操作 能具备遵循国际象棋的真实走棋规则的能力。
(5) 提子(针对围棋):给定“棋手、一个位置的横纵坐标”,将该位置上的 对手棋子移除。需要考虑处理异常情况,例如:该位置超出棋盘的范围、 该位置无棋子可提、所提棋子不是对方棋子等。——注:无需考虑实际的 提子规则,但你可以扩展该 spec 让你的该操作能具备遵循围棋的真实提 子规则的能力。
(6) 吃子(针对国际象棋):给定“棋手、两个位置横纵坐标”,将第一个位 置上的棋子移动至第二个位置,第二个位置上原有的对手棋子从棋盘上 移除。需要处理异常情况,例如:指定的位置超出棋盘的范围、第一个位 置上无棋子、第二个位置上无棋子、两个位置相同、第一个位置上的棋子 不是自己的棋子、第二个位置上的棋子不是对方棋子等。——注:无需考 虑实际的吃子规则,但你可以扩展该 spec 让你的该操作能具备遵循实际 国际象棋吃子规则的能力。
在完成上述功能时,除了类名已确定无需修改,属性和方法的名字、数据类 型可自由设计,方法的输入参数也可自行设计。若需要其他的辅助类,也请自行 设计。
写一个基于命令行的主程序 MyChessAndGoGame.java,在 其 main()实现以 下功能:
(1) 让用户选择创建一盘国际象棋或一盘围棋,用户输入“chess”或“go” 分别代表国际象棋和围棋;让用户输入两个玩家的名字;
(2) 启动比赛,程序提示玩家双方交替采取行动,直到一方输入“end”而结 束。双方分别采取行动的时候,可以选择以下行为之一,也可以选择“跳 过”(即放弃本次采取行动的权利):
⚫ 将尚未在棋盘上的一颗棋子放在棋盘上的指定位置;
⚫ 移动棋盘上某个位置的棋子至新位置;
⚫ 提子或吃子;
⚫ 查询某个位置的占用情况(空闲,或者被哪一方的什么棋子所占用);
⚫ 计算两个玩家分别在棋盘上的棋子总数。 请自行为用户设计针对上述行为所需输入的数据,用户输入越简洁越好。
(3) 当某一方输入 end 结束游戏之后,双方可以查看本次比赛的走棋历史, 即能够查询自己所走的所有步骤。
注:本次任务并非完整实现围棋和国际象棋的所有规则,甚至有些要求与实 际的棋类规则有冲突,请严格按照上述说明进行设计,无需扩展。
4、Multi-Startup Set (选做)
请阅读 http://web.mit.edu/6.031/www/fa18/psets/ps2 ,遵循该页面内的要求完 成编程任务。
三、正文
1、Poetic Walks
这个任务主要考察了抽象数据类型(ADT)和面向对象(OOP)的编程方法。要求自己实现Graph抽象类和具体类,类似于Java中的高级抽象类List、Set与其具体实现的关系。另外,测试代码也需要自己编写。
ADT方面考察可变变量与不可变变量,OOP考察了继承、抽象类、重载、变量保护等知识,总体难度不是特别大,但是细节内容比较多,要求也比较繁杂,但所考察内容确实是Java编程与软件构造必要的技术。
总的来说,编写完测试后通过自己编写的String Graph到泛型Graph,实现“诗意的漫步”,也就是类的应用。
Problem 1
Problem 1要求首先编写Graph类的测试,包括对其静态方法和实例化方法的测试。当然,这个工作是在具体编写Graph类之前进行的,编写好测试后,后面编写的各种Graph类就可以进行检验。
主要的实现在测试类GraphInstanceTest中,至于GraphStaticTest暂时不需要修改。任务也比较明确,完成Testing strategy后编写Graph类中实例方法的测试即可。其中已编写好了testInitialVerticesEmpty,相应的根据自己的设计添加测试函数并编写具体代码。
观察Graph的所有实例化方法后,分别添加了testVerticesChanged、testSources、testTargets、testAdd、testSet以及testRemove方法。依次用来检测点集的变化,检测边来源、目标获取方法,检查添加点和边以及删除点的方法。测试的代码也比较简单,比如检测点集变化就是添加点、删除点,过程中不断检查点的数量,边来源与目标通过与正确结果比较即可,添加与移除点暂时通过数量来判断。而set方法的测试则需要Source和Target并对权值进行检验。
另外,由于类中具体的方法在后面的任务进行编写,所以测试结果暂无。
Problem 2
从这个部分起,要具体实现基于接口Graph的String作为标签的具体类。而这个部分的任务则是实现一个基于边关系的图,并重写接口Graph中的方法。另外要求里需要编写一些AF、RI和rep exposure相关的说明,这里便不再解释。后面ConcreteVerticesGraph类的实现很多地方类似ConcreteEdgesGraph ,所以基本思路这里详细介绍下。
(Problem3要求用L实现,这里代码事实上是已经更改过的,自行把L替代为String即可
private final Set<L> vertices = new HashSet<>();
private final List<Edge<L>> edges = new ArrayList<>();
对于ConcreteEdgesGraph有vertices和edges两个成员变量,为了安全性考虑,都设置为private final。前者是String类型的集合,后者是Edge的List。而Edge也是需要实现的类,这里先介绍它的实现思路。
Edge的成员变量如下:
private final L source;
private final L target;
private final int weight;
构造函数和相应的get方法比较常规就不再介绍。要注意一点,因为要求Edge实现为不可变类,所以成员变量首先要设置为private final,然后为了方便ConcreteEdgesGraph类进行调用,最好重载一下equals和hashcode函数,重载方法如下:
@Override public boolean equals(Object obj) {if (obj instanceof Edge) {Edge c = (Edge) obj;return source.equals(c.source) && target.equals(c.target) && weight == c.weight;}return false;}@Override public int hashCode() { return source.hashCode() + target.hashCode() + new Integer(weight).hashCode(); }
而作为不可变类,mutator method就不需要了。
下面回到ConcreteEdgesGraph类,add方法的核心是vertices.add(vertex),但在这之前需要进行判断,首先参数vertex不为null,然后遍历vertices中是否已有,如果有返回false,遍历结束后加入即可,返回true。
set方法首先要对参数是否有效进行判断,然后将source和target加入到vertices,根据上面add的设定,如果已存在则不会添加,所以无需担心。添加完以后遍历边集,如果两点间有权值与当前不相等的变量则移除并添加新的,不修改是由于Edge是不可变类。
remove方法先通过contain判断一下是否存在,如果不存在则返回false,否则移除,并且遍历边集,如果有首或尾是该点的直接移除。
vertices方法要注意返回unmodifiableSet,从而避免rep exposure。
sources和targets的实现思路类似,遍历边,起点或终点满足条件的加入Map然后返回Collections.unmodifiableMap。
编写过程中遇到一些问题,首先是重写equal时为什么常常要重写hashcode,原因是为了有利于get或者put时可以更好的根据哈希码来计算存储位置。
另外要区分contains和containsAll,并且其底层采用的equal进行比较而不是双等号。所以很多时候重写equal方法很有必要。
最后是一个小细节,上面提到过,为了避免代表泄露,常常需要Collections.unmodifiableMap。
同样是实现图,这次以点为核心进行实现,所以首先介绍下Vertex的实现思路。与Edge不同,Vertex是可变类,也就是说可以修改内部值。构造方法和get方法就不再具体解释,但尽管是可变类,只是提供mutator方法,为了内部安全还是需要把成员变量定义为private final,get方法也要注意使用Collections.unmodifiableMap。
下面介绍一下mutator的实现。首先要提供addSource、addTarget、removeSource和removeTarget方法,首先判断一下是否containsKey然后进行相应的操作,防止不存在还运行remove方法。
另外equal和hashcode还是需要重写一些,方法类似于ConcreteEdgesGraph类。
private final List<Vertex<String>> vertices = new ArrayList<>();
下面介绍一下ConcreteVerticesGraph的具体实现,思路类似于ConcreteEdgesGraph。add方法实现思路与ConcreteEdgesGraph一样,不再解释。set稍有不同,因为现在的主体是Vertex而非Edge。遍历点集,如果等于source或target便调用相应的addTarget或addSource方法,最后返回权重即可。
remove函数同样遍历点集,如果是删除点则直接删除,否则移除其source或Target。最后返回移除结果。
vertices函数不能直接Collections.unmodifiableSet(set)了,因为成员变量是List,所以遍历添加一下即可。
sources和targets函数遍历即可,找到相应的vertex然后调用其getSources或getTargets函数,再返回Collections.unmodifiableMap。
实现过程中有一点要注意,在遍历删除满足条件的点时,要使用迭代器防止出现问题,不过仅仅移除一个点便无所谓,但是这个点还是要注意,在其他遍历中可以防止出现奇怪的错误。
Problem 3
这个部分的任务是将之前实现的String标签的Graph泛型化,能够以其他类型作为标签类型。首先需要做如下更改:
public class ConcreteEdgesGraph<L> implements Graph<L> { ... }class Edge<L> { ... }
public class ConcreteVerticesGraph<L> implements Graph<L> { ... }class Vertex<L> { ... }
从而,根据L的不同Graph中的数据类型便不同。在此基础上,还需要将所有String改为L。
使用过程中需要注意一点,原有的Edge与Vertex需要更改为Edge以及Vertex,而不是仅仅将String替换为L。更改结束后,便可通过之前编写的JUnit测试进行测试。
对于Graph.empty(),这个静态方法的编写要求比较简单,只需要选择一种上面实现的ConcreteGraph即可。但反映的编程思想却很深刻,首先通过静态函数创建实例,或者说静态工厂。其次通过这种方式,无论内部采用哪种Graph都不影响效果,用户看不到内部实现,体现了抽象和封装的思想。
另外,为了保证其可以应用与多种数据类型,还需要完善GraphStaticTest中的测试,即L选为其他类型进行测试。
Problem 4
第一个任务是为后来编写好的GraphPoet类编写测试。根据GraphPoet类的注释可以了解其原理,即将输入的文字里面的单词邻接关系构建为图,邻接次数越多边的权重越大,然后寻找最大权重的双边路径,来预测和补全句子。这样,可以使用注释里的测试用例:
通过“This is a test of the Mugar Omni Theater sound system.”将“Test the system.”转换为“Test of the system.”。
根据上述分析,得到实现代码:
GraphPoet graphPoet = new GraphPoet(new File("src/P1/poet/mugar-omni-theater.txt"));
assertEquals("Test of the system.", graphPoet.poem("Test the system. "));
GraphPoet的实现思路比较清晰,首先读取文件,并按照其内容通过split方法处理后构件图,注意要使用toLowerCase(),因为题目中要求对大小写不敏感。构建图的过程即遍历句子,将相邻的词写入图中生成边。
图构建好以后编写poem方法,即“写诗”的方法。遍历输入,如果相邻的句子在图中存在二边路径则排序获得路径权值最大的路径中间的词,写入结果。
构建过程中采用了Integer包装类,为了能对null情况作出反应而不是像使用int产生异常。
Integer weight = graph.targets(words[i - 1].toLowerCase()).get(words[i].toLowerCase());
if (weight == null) weight = 0;
为了获取二边路径编写了方法:
private Map<String, Integer> getTwoEdgeLongPaths(String src, String dest);
即通过targets来寻找所有二边路径,返回后进行排序。排序过程可以通过Collections的方法实现:
List<Map.Entry<String, Integer>> list = new ArrayList(map.entrySet());
list.sort((o1, o2) -> (o2.getValue() - o1.getValue()));
另外,在构建“诗句”的过程需要频繁的更改字符串,使用StringBuilder显然更好,可以节约空间。
2、Re-implement the Social Network in Lab1
P2要求利用P1中实现的图来重新实现Lab1中的Social Network。因为在P1中已经实现为泛型,所以可以很好的解决社交网络的问题。只需要把L也就是类型变量设置为Lab1中编写的Person类,再根据要求完善一些方法即可。
基于P1实现的Graph重新实现Lab1中的社交网络,可以采用继承的方式,利用父类Graph的set、add、remove等方法实现addVertex、addEdge、getDistance等方法。
addVertex比较简单,直接调用add方法即可,至于各类判断在Graph内都已经写好。
public void addVertex(Person vertex){ add(new Person(vertex.getName())); }
同样,addEdge也可以通过调用Graph中的方法,通过set即可添加边:
public void addEdge(Person src, Person dest) { set(new Person(src.getName()), new Person(dest.getName()), 1); }
getDistance可以根据Lab1中已经完成的广度优先搜索进行修改得到,只要对应相应的方法即可。
实现过程中遇到一个问题,public class FriendshipGraph extends ConcreteEdgesGraph发生错误,提示没有默认构造函数,后来发现是ConcreteEdgesGraph中编写的无参构造函数权限修饰符设置有问题导致继承出现问题,修改为protected子类即可继承。
Person类的核心在于其姓名,为了保证代表不泄露,要设置属性name为private final,使之成为不可变类。另外构造函数也比较简单,然后再编写一下get方法即可。但注意不能编写mutator method。另外,需要重写equal和hashCode从而保证其可以正常比较。
对于Person类主要要帮助变量不泄露,防止被修改,谨慎编写get方法和构造方法,并且要适度的重写方法。
对于main函数,根据题目要求,创建关系图,然后实例化rachel、ross、ben、kramer四个Person,然后加入相应的点与边关系,再通过getDistance获得距离,依次输出1、2、0、-1。
测试过程,首先测试addVertex函数,创建一个空的关系图,然后通过assertEquals判断点集的大小是不是0,然后实例化一个Person对象,加入到graph中,再次通过assertEquals判断,这次判断点集的大小是不是1。
然后测试addEdge函数,同样先创建一个空的关系图,然后通过assertEquals判断其值是不是0。接下来创建两个Person,并将这两个节点作为点加入关系图中,然后addEdge,并通过assertEquals判断边的数量是不是1。
最后测试一下距离函数,使用了题目要求给出的用例,创建四个人,分别是rachel、ross、本、和kramer,然后再rachel和ross,ross和ben之间添加边,最后分求rachel和ross,rachel和ben、rachel和rachel,rachel和kramer之间的距离,依次应该是1,2,0和-1。测试结果如下:
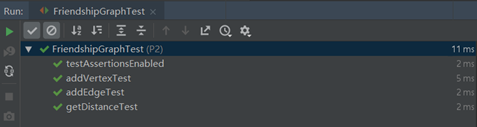
3、Playing Chess
基本ADT
为了实现P3要求,分别设计了Position、Player、Piece、Board、Action、Game等ADT。ADT均重写了equal、hashCode、toString方法。具体如下:
Position类代表棋子的位置,具有x,y坐标两个成员变量,属于不可变类。总体实现较为简单,只提供get方法而不提供set方法,保证其是不变类。
Player类表示一场棋类游戏中的玩家,具有name与actions两个常用遍历,后者记录其在游戏中的操作。因为提供了添加操作即addAction的方法,所以是可变类。
Piece类表示棋子,含有棋子的相关信息。成员变量包括其标签,而标签的类型是可变的,也就是说Piece是泛型,但必须是枚举类型,含有游戏的所有标签,例如国际象棋就是King、Queen、Rook等,而围棋则是Black、White等。最后一个成员变量则是owner,记录其所有者,类型是Player。
为了方便移动、吃子操作,编写了changePosition方法,用来更改棋子的位置,所以可以知道,Piece是可变类。
Board类是可变类,其成员变量包括size、pieces、IsCrossPointBoard,依次表示棋盘的大小、棋盘上棋子的列表、棋是否是下在对角线上。其checkRep也相对复杂。
除了基础的get类(经过防御性拷贝),提供了addPiece、removePiece、movePiece、eatPiece这四个mutator方法,以及getPieceByPosition方法,方便获取棋盘某个位置上的棋子状态(是否存在棋子、存在的棋子所有者是谁)。最后还编写了getPieceNum方法,用于计算某玩家在棋盘上拥有的棋子数量。
Action类是不可变类,用于记录某个操作的信息,成员变量有操作的发起者、操作类型(添加、删除、移动、吃子四种)、操作对象、新的位置(当添加和删除时为null)。
为了保证其不可变性,get方法加入了防御性拷贝。Action本身可以通过Game 的act方法进行解析与执行。
Game方法通常是以父类存在,被具体的棋类继承,是可变类。成员变量有board、players、actions,依次代表本次游戏的棋盘、玩家和操作。其成员变量均经过了防御性拷贝。核心方法是act方法,用于解析和执行action,从而对棋盘上的棋子进行相应的操作,并对不合法的操作返回false。
为了便于继承,其成员变量与checkRep均设置为protected。
为了实现MyChessAndGoGame首先基于上面实现的ADT实现了以下枚举类ChessGamePieceTags和GoGamePieceTags,记录两类游戏的棋子标签。并通过继承Game类实现了ChessGame和GoGame类,其中ChessGame重写构造函数并将32个国际象棋棋子在初始化时加入,GoGame增强了checkRep的判断,保证黑白子的拥有者依次为玩家A和玩家B,两种棋类均在构造函数中初始化棋盘,从而符合对应棋类的要求。
主程序设计
在此基础上,实现了主程序MyChessAndGoGame。
根据实验指导要求,首先输入棋的类型,并对不合法的输入进行判断,这里通过while实现,然后依次输入两个玩家的姓名,这里同样有合法输入判断,例如不为空,不重复。下面,根据玩家选择的棋类对相应输入规则进行提示。
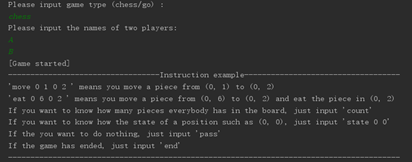
然后,玩家A和玩家B就可以轮流输入指令执行进行下棋,直到有一方输入了end。根据要求,允许玩家进行某个位置棋子状态的查询、棋盘上双方棋子数量的查询以及跳过指令。
根据不同的棋类有不同的方法,例如move和eat对围棋无效,add和remove对国际象棋无效,会要求重新输入。
最后,玩家输入end后游戏结束,并会输出本次游戏两者的相关操作。
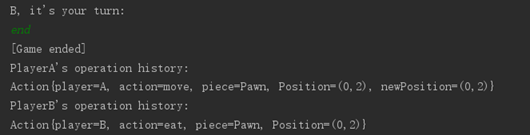
为了将用户输入映射到ADT的具体方法,在循环中加入了if语句进行判断,对各类操作分别处理。例如“end”会直接跳出循环,count会调用game中board变量的getPieceNum进行棋子计数,state会调用board的getPieceByPosition获取某个位置的棋子信息,如果返回值为null则输出不存在棋子的相关提示。
对于具体的操作,例如add、remove、move、eat都会通过board的act方法进行执行,首先根据用户的输入实例化一个Action,然后根据Action执行相应操作,如果返回值为false则要求重新输入。
举个例子,对于移动棋子操作:
if (!game.act(new Action<ChessGamePieceTags>(currentPlayer, Action.actionType.eat, piece, newPosition))){System.out.println("Wrong src or dest.");continue;
}
测试类
基本的测试策略及模块化测试,对具体棋类及棋类游戏涉及到的添加、删除、移动、吃子四个操作进行测试,从而保证主程序的功能的能够实现。
测试过程中采用简单的例子,可以判断方法是否正常工作。
在测试类的成员变量中实例化GoGame和ChessGame两类游戏以及四个玩家,保存涉及到的位置对象、棋子对象,并分别对其功能进行测试。
例如对GoGame中的“add”方法,首先实例化相关Action并在game的act方法中进行解析与执行,然后判断棋子数量和两个玩家拥有的棋子数量,按照预期,棋子数量应该为1,并且只有playerA的棋子数量为1。随后,给playerB添加白子,同样判断数量的变化,此时棋盘上棋子的数量应为2,两个玩家都有1个棋子。
对remove的测试相对简单,首先给playerA添加一个棋子,然后让playerB对其进行remove,随后再次判断棋盘中棋子的数量。根据预期,两次的结果应该依次为1和0。
下面对ChessGame中的move方法进行测试,首先实例化两个位置,位置A和C最初有棋子,位置B没有棋子。然后通过getPieceByPosition获取位置A的棋子后对其进行移动,判断其不为null。经过判断,可以确定三个位置是否有棋子,然后执行act方法,移动棋子至C位置,由于有棋子,按照预期会返回false,而移动到B则可以成功移动,返回true。最后,再次判断A与B两个位置是否存在棋子,根据预期,位置A不再存在棋子,而位置B存在棋子。
最后对ChessGame的Eat方法进行测试,同样选择两个位置,这两个位置都有棋子,然后通过getPieceByPosition获取棋子,判断B位置棋子的拥有者为第二个玩家,然后实例化对应Action并执行,此时B位置的棋子已经被第一个玩家的A位置棋子吃掉,所以再次判断B位置棋子的拥有者,按照预期,B位置的棋子的拥有者为第一个玩家。既然发生了“吃子”操作,此时A位置按照预期已经不存在棋子,B位置存在气质,分别判断这两个位置是否存在棋子即可。
通过对四个基本棋类操作测试,基本可以保证主程序相应方法的正确执行。
测试结果如下:
4、Multi-Startup Set (选做)
(时间原因,并没有完成P4)
这篇关于【软件构造】实验笔记(二)Lab2-Abstract Data Type and Object-Oriented Programming的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







