统计学习方法：罗杰斯特回归及Tensorflow入门

本文主要是介绍统计学习方法：罗杰斯特回归及Tensorflow入门，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

作者：桂。

时间：2017-04-21 21:11:23

链接：http://www.cnblogs.com/xingshansi/p/6743780.html

前言

看到最近大家都在用Tensorflow，一查才发现火的不行。想着入门看一看，Tensorflow使用手册第一篇是基于MNIST的手写数字识别的，用到softmax regression，而这个恰好与我正在看的《统计信号处理》相关。本文借此梳理一下：

　　1）罗杰斯特回归

　　2）Softmax Regression

　　3）基于Tensorflow的MNIST手写数字识别框架

内容为自己的学习记录，其中多有借鉴他人的地方，最后一并给出链接。

一、罗杰斯特回归（Logistic Regression）

　　A-问题描述

一般说的Logistic回归，是指二分类问题。

对于连续的变量X，如果说它服从Logistic回归，则：

对应概率密度以及分布函数：

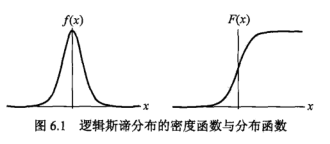
F(x)更像是一个threshold，f(x)的表达式也利于求导。

定义Logistic 回归模型：

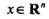为输入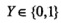，为对应输出，二项Logistic回归对应如下模型：

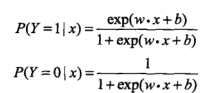
联系到之前写的感知机：

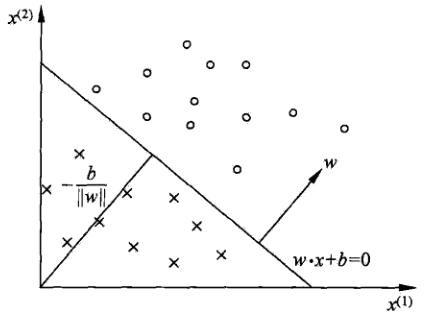
分类时，对应概率：

为正的概率大，为负的概率小，这个指数有点像把正/负→进行指数处理，这样就容易理解了。

有时为了表示方便，记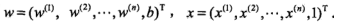：，则表达式简化为：

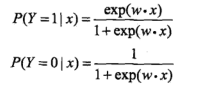
为什了叫Logistic regression呢？

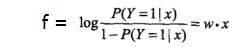
这样明显是一个线性回归的表达式。

　　B-理论分析

对于参数的求解，同感知机一样，就是求解w。利用最大似然求解：

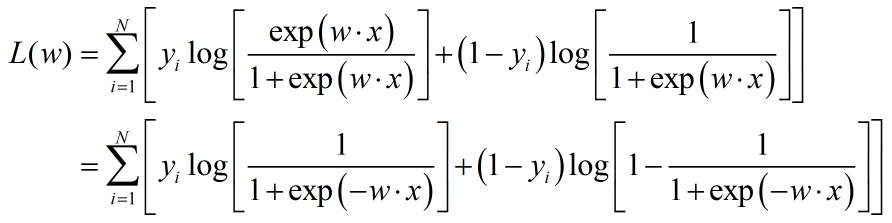
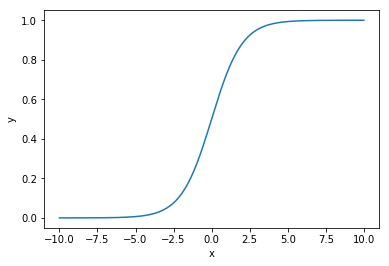
定义sigmoid函数：

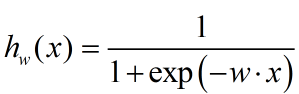
准则函数重新写为：

可以借助梯度下降或者牛顿法，这几个方法之前已经有过介绍。

利用求解得到的w，即可以进行概率判断，哪个概率大就判给哪个类别，整个思路与感知机也是一样的：

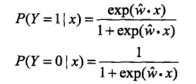
　　C-理论应用

用一个code说明其工作原理，还是借助之前感知器用的例子，因为Logistic回归可以认为是Softmax回归的特例，这里借用softmax框架给出对应代码：

%Logistic regression
clear all; close all; clc;
%Every category samples
N = 100;
X = [randn(N,2)+2*ones(N,2);...randn(N,2)-2*ones(N,2)];
figure;
subplot 121
label = [ones(N,1);2*ones(N,1)];
plot(X(label==1,1),X(label==1,2),'b.');hold on;
plot(X(label==2,1),X(label==2,2),'r.');hold on;
%%Train
numClass = 2;
parm.learningRate = 0.5;
pram.iter = 5000;
parm.precost = 0;
X = [ones(size(X,1),1), X]';
[nfeatures, nsamples] = size(X);
W = zeros(nfeatures, numClass);
% 1, 2, 3 -> 001, 010, 100.
groundTruth = full(sparse(label, 1:nsamples, 1));
for i = 1:pram.iterrsp = W'*X;rsp = bsxfun(@minus, rsp, max(rsp, [], 1));rsp = exp(rsp);prob = bsxfun(@rdivide, rsp, sum(rsp));% compute gradient based on current probabilitygrad = - X * (groundTruth - prob)' / nsamples ;% update WW(:,2:end) = W(:,2:end) - parm.learningRate * grad(:,2:end);% compute costlogProb = log(prob);idx = sub2ind(size(logProb), label', 1:size(logProb, 2));parm.cost = - sum(logProb(idx)) / nsamples;if i~=0 && abs(parm.cost - parm.precost) / parm.cost <= 1e-4break;endparm.precost = parm.cost;
end
%Predict
rsp = W' * X; 
[~, prediction] = max(rsp, [], 1); 
subplot 122
X = X(2:end,:)';
plot(X(prediction==1,1),X(prediction==1,2),'b.');hold on;
plot(X(prediction==2,1),X(prediction==2,2),'r.');hold on;
x = -5:.1:5;
b = W(1,2);
y = -W(2,2)/W(3,2)*x-b/W(3,2);
plot(x,y,'k','linewidth',2);

　　对应结果图：

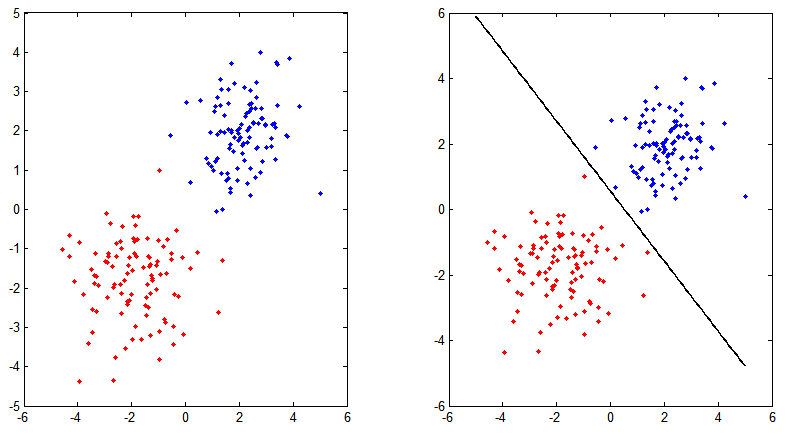
二、Softmax 回归

Logistic回归分析的是两类，对于多类的情形，通常称为：Softmax 回归。基于概率所以soft，概率中最大值所以Max。

其实这个式子可以理解为Y=K时，$w_k*x = 0$，上面式子可以表述为，为了与下面表述一致，这里w改为$\theta$表示：

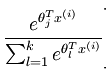
假设样本个数为m,同logistic回归类似，Softmax准则函数可以写为：

进一步写为：

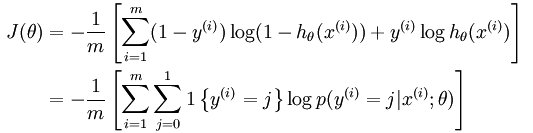
思路同Logistic回归，同样利用梯度下降/牛顿-Rapson可以求解。求解出w：

其中，

分类的思路与Logistic回归也是完全一致。另外在求解的时候，可以发现：

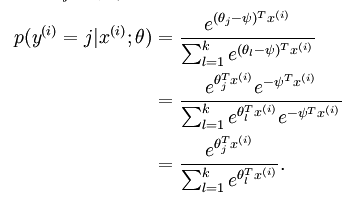
求解的时候，都减去一个数，是不影响结果的。前面提到Y=K时，$w_k*x = 0$，其实有一个为零就行，哪一类是无所谓的，所以优化只优化K-1，给出代码：

%Test Softmax Regression
clear all; close all; clc;
N = 100;
X = [randn(N,2)+5*ones(N,2);...randn(N,2)-1*ones(N,2);...randn(N,2)-4*ones(N,2)];
figure;
subplot 121
label = [ones(N,1);2*ones(N,1);3*ones(N,1)];
plot(X(label==1,1),X(label==1,2),'b.');hold on;
plot(X(label==2,1),X(label==2,2),'r.');hold on;
plot(X(label==3,1),X(label==3,2),'k.');hold on;
title('Orignal Data')
%%Train
numClass = 3;
learningRate = 0.5;
X = [ones(size(X,1),1), X]';
[nfeatures, nsamples] = size(X);
W = zeros(nfeatures, numClass);
% 1, 2, 3 -> 001, 010, 100.
groundTruth = full(sparse(label, 1:nsamples, 1));
iter = 5000;
precost = 0;
for i = 1:iterrsp = W'*X;rsp = bsxfun(@minus, rsp, max(rsp, [], 1));rsp = exp(rsp);prob = bsxfun(@rdivide, rsp, sum(rsp));% compute gradient based on current probabilitygrad = - X * (groundTruth - prob)' / nsamples ;% update WW(:,2:end) = W(:,2:end) - learningRate * grad(:,2:end);% compute costlogProb = log(prob);idx = sub2ind(size(logProb), label', 1:size(logProb, 2));cost = - sum(logProb(idx)) / nsamples;if i~=0 && abs(cost - precost) / cost <= 1e-4break;endprecost = cost;
end
%Predict
rsp = W' * X; 
[~, prediction] = max(rsp, [], 1); 
subplot 122
X = X(2:end,:)';
plot(X(prediction==1,1),X(prediction==1,2),'b.');hold on;
plot(X(prediction==2,1),X(prediction==2,2),'r.');hold on;
plot(X(prediction==3,1),X(prediction==3,2),'k.');hold on;
title('Prediction')

　对应结果（线性可分时，结果正确，线性不可分时，边界点容易出现错误，如下图）：

而实际应用中，我们不愿将任何一个$\theta$直接置零，而是保留所有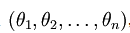，但此时我们需要对代价函数做一个改动：加入权重衰减。准则函数变为：

这个时候只要将上面对应的code按如下修改即可：

    grad = - X * (groundTruth - prob)' / nsamples +.02 * W;%lamdba = 0.02
%     grad = - X * (groundTruth - prob)' / nsamples ;% update W
%     W(:,2:end) = W(:,2:end) - learningRate * grad(:,2:end);W = W - learningRate * grad;

三、基于Tensorflow的MNIST手写数字识别

MNIST数据库是一个手写数字识别数据库，

MNIST(Mixed National Institude of Standards and Technology database)，由几万张图片组成，其中每个照片像素为28*28（在读取时已经被拉成28*28=784的向量了），训练数据集train：55000个样本，验证数据集validation：5000个样本，测试数据集：10000个样本。

首先分别读取训练和测试数据：

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

　　先看看数据长什么样，任意读取一张图片：

#imshow data
imgTol = mnist.train.images
img = np.reshape(imgTol[1,:],[28,28])
plt.imshow(img)

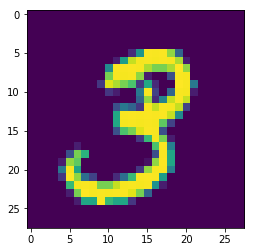
大概就是这个样子（其实是个gray图）.

下面开始对数据进行基于Softmax Regression的处理。

首先创建一个会话（session），为什么需要创建session可以参考Tensorflow基本用法：

import tensorflow as tf
sess = tf.InteractiveSession()

　　通过为输入图像和目标输出类别创建节点，来开始构建计算图：

sess = tf.InteractiveSession()
x = tf.placeholder("float", shape=[None, 784])
y_ = tf.placeholder("float", shape=[None, 10])

　　其中'None'表示该维度大小不指定。

我们现在为模型定义权重W和偏置b。可以将它们当作额外的输入量，但是TensorFlow有一个更好的处理方式：变量。一个变量代表着TensorFlow计算图中的一个值，能够在计算过程中使用，甚至进行修改。在机器学习的应用过程中，模型参数一般用Variable来表示：

W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))

　　变量需要通过seesion初始化后，才能在session中使用。这一初始化步骤为，为初始值指定具体值（本例当中是全为零），并将其分配给每个变量,可以一次性为所有变量完成此操作：

sess.run(tf.initialize_all_variables())

　　初始化完成后，接下来可以实现Softmax Regression了：

y = tf.nn.softmax(tf.matmul(x,W) + b)

　　softmax是tf.nn下的一个函数，tf.nn包含了很多神经网络的组件，tf.matmul在tensorflow里的意义是矩阵相乘。给出损失函数（交叉熵）：

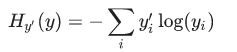
交叉熵没听过其实也不要紧，Maximum Likelihood（ML, 最大似然）估计应该都知道吧？

其中N为样本总数，且

我们频数以及频率是观测得到的，如何估计概率呢？我们通常用最大似然：

如果变形一下呢？同除以N：

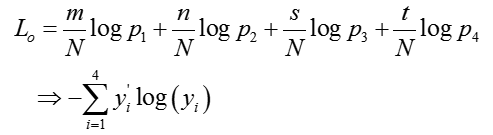
最大似然估计不就是最小交叉熵估计？另一方面，交叉熵对误差的衡量类似联合概率密度的作用。给出对应code:

cross_entropy = -tf.reduce_sum(y_*tf.log(y))

　　reduce.sum为求和，reduce.mean为求取均值。有了准则函数以及理论框架，利用梯度下降进行训练：

train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

　　这里利用小批量梯度mini-batch下降,batch = 50个训练样本:

for i in range(1100):batch = mnist.train.next_batch(50)train_step.run(feed_dict={x: batch[0], y_: batch[1]})

　　训练后进行预测并打印：

correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

　　给出总的code:

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)#imshow data
#imgTol = mnist.train.images
#img = np.reshape(imgTol[1,:],[28,28])
#plt.imshow(img)sess = tf.InteractiveSession()
x = tf.placeholder("float", shape=[None, 784])
y_ = tf.placeholder("float", shape=[None, 10])
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
sess.run(tf.global_variables_initializer())
y = tf.nn.softmax(tf.matmul(x,W) + b)
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
for i in range(1100):batch = mnist.train.next_batch(50)train_step.run(feed_dict={x: batch[0], y_: batch[1]})correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

　　预测结果为：91.56%.

参考：

Softmax regression:http://deeplearning.stanford.edu/wiki/index.php/Softmax_Regression
李航：《统计学习方法》
Tensorflow官网文档：https://www.tensorflow.org/get_started/mnist/beginners
http://tensorfly.cn/tfdoc/tutorials/mnist_pros.html

这篇关于统计学习方法：罗杰斯特回归及Tensorflow入门的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！