4. 机器学习基石-When can Machine Learn? - Feasible of Learning

When can Machine Learn? - Feasible of Learning

• When can Machine Learn? - Feasible of Learning
  
  • 1. Learning is Impossible?
  • 2. Probability of the Rescue
    
    • 1) Hoeffding Inequity
    • 2) Connection Between Hoeffding Inequity and Learning
    • 3) Connection Between Hoeffding Inequity and Real Learning
      
      • ① Introduction of Bad Data
      • ② Probability of Bad Data
• Summary
• Reference

这章主要讨论 Whether machine learning is possible or not.

1. Learning is Impossible?

在讨论之前，先看下面的一个问题

这类似于一道智商题,却没有标准答案，根据你不同的一个视角，可以找到不同的规则。比如：

1. 左上角的正方形是否涂黑
2. 是否对称
3. 正中间的正方形是否涂黑
4. …

所以无论机器学到的是什么模型，其他人都能说机器说错了。也就是说机器不能真的学习了。

2. Probability of the Rescue

1) Hoeffding Inequity

上面提到了机器不能学习，因为机器求出来的假设函数$g(x)$很难与目标函数$f(x)$一样：因为数据不一样。 但是根据Hoeffding不等式（公式1），可以证明，在数据量足够大的情况，可以保证$g(x)$很接近于

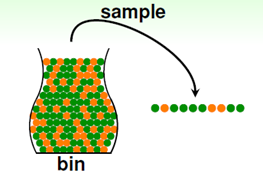
其中 $\rho$为概率符号， $\lvert \nu - \mu \rvert$表示2个值的近似程度， $\epsilon$是这个近似程度的下界， $N$为样本数量的大小，所以不等式的意思是两个值的差别大于 $\epsilon$的概率小于等于 $2 \cdot \exp \left( -2 \epsilon^2 N \right)$。所以，如果当 $\epsilon$一定的情况下， 随着样本数量 $N$越大，那么这个差距的可能性越小（参考 $e^{-n}$ 的曲线），当 $\epsilon$很小且 $N$大到一定的程度的时候，$\mu$和 $\nu$差别很小的概率很低，即 $\mu$和 $\nu$相等是一个大概近似正确（Probably Approximately Correct, PAC)的情况。

下面举例说明公式的意义（以概率统计中的从罐子中有放回的取球为例)，如图二。

图二 Sampling^[2]

罐子中只有橙色和绿色的球，其中橙色球的概率为 $\mu$,那么绿色球的概率为 $1-\mu$， 如果通过抽样，得到橙色球的概率为 $\nu$，那么绿色球的概率为$1-\nu$（其中，$\mu$是假设的，是未知的，$\nu$而是通过抽样得到的，已知的)。因为抽样的罐子是均匀是，所以抽样得到的橙色球的概率 $\nu$要近似于实际罐子中橙色球的概率 $\mu$。这个近似值得范围就是Hoeffding Inequity所表示的

2) Connection Between Hoeffding Inequity and Learning

下面引用PPT里面的对比图来进行解释。

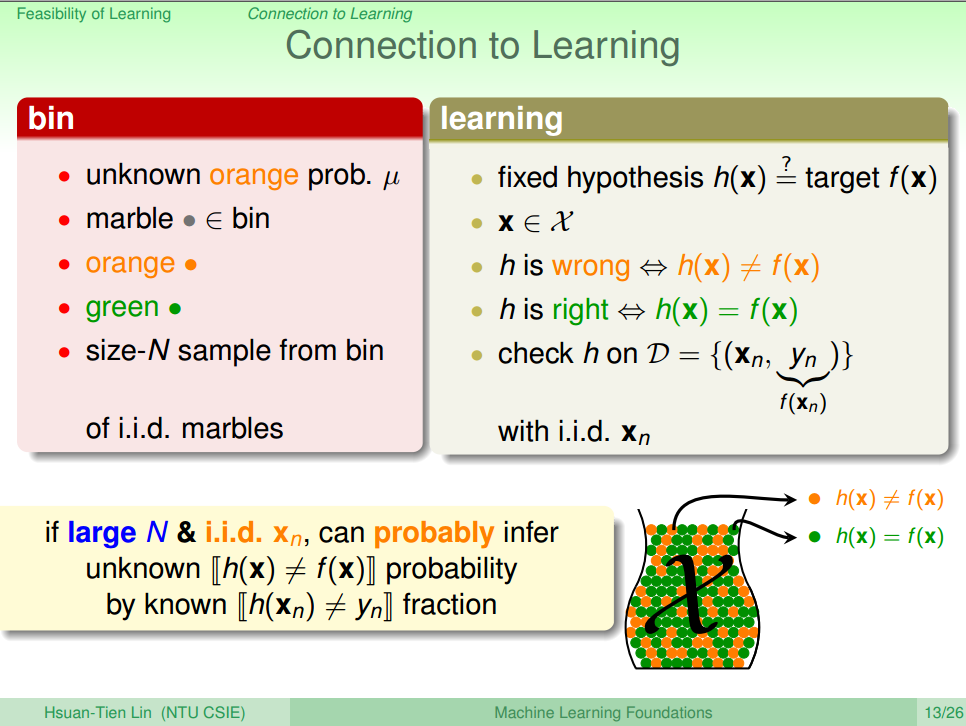
图三 Connetion to Learning ^[3]

上面的抽样调查中，我们关键有： 罐子中橙色球的实际概率 $\mu$, 抽样出来的球 ∈ 罐子，抽样的橙色球概率，抽样得到的绿色球概率
对应到实际学习中就是： 实际测试中$h(x) \neq g(x)$ 的概率 $E_{out}$, 训练样本$x$ ∈ 整个数据集 $X$，训练过程中满足 $h(x) \neq g(x)$ 的概率 $E_{in}$, 训练过程中满足 $h(x) = g(x)$ 的概率 $1-E_{in}$,

并且可以得到以下公式（2）和公式（3）

$$\nu = \frac{1}{N} \cdot \sum\limits_{i=1}^N \left[\left[ h(x_i) \neq f(x_i) \right]\right] \quad (x_i ∈ X) \tag{$2$}$$

$$\mu = \epsilon \cdot \sum\limits_{i=1}^N \left[\left[ h(x_i) \neq f(x_i) \right]\right] \tag{$3$}$$

$\epsilon$表示为期望值，即实际样本中的错误率 $E_{out}$

为了查看方便，列个表格进行说明

罐子	机器学习
罐子中橙色球的实际概率 $\mu$	实际测试中$h(x) \neq g(x)$ 的概率 $E_{out}$
抽样出来的球 ∈ 罐子	训练样本$x$ ∈ 整个数据集 $X$
抽样的橙色球概率	训练过程中满足 $h(x) \neq g(x)$ 的概率 $E_{in}$
抽样得到的绿色球概率	训练过程中满足 $h(x) = g(x)$ 的概率 $1-E_{in}$,

因此结合Hoeffding的理论支持后，我们可以扩展机器学习的流程图，如图四所示。

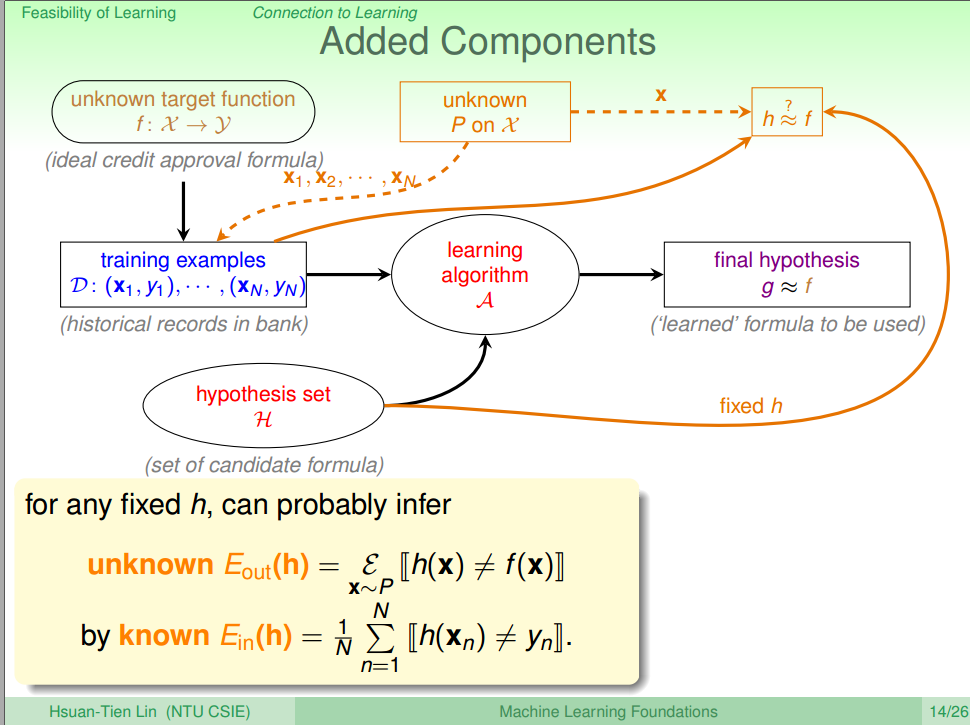
图四 New Learning Diagram ^[3]

其中虚线表示未知概率 $\rho$ 对随机抽样以及实际测试中$h(x) \neq g(x)$ 的概率 $E_{out}$ 的影响，实线表示训练过程中满足 $h(x) \neq g(x)$ 的概率 $E_{in}$。

上面提到的$E_{in}$ $E_{out}$ 可以分别用下面的公式（4）（5）表示

$$E_{in} = \nu = \frac{1}{N} \cdot \sum\limits_{i=1}^N \left[\left[ h(x_i) \neq f(x_i) \right]\right] \quad (x_i ∈ X) \tag{$4$}$$
$$E_{out} = \mu = \epsilon \cdot \sum\limits_{i=1}^N \left[\left[ h(x_i) \neq f(x_i) \right]\right] \tag{$5$}$$

所以Hoedding的不等式可以变成公式（6）
接近于

$$f(x)$.$$
\rho \left[ \lvert E_{in} - E_{out} \rvert > \epsilon\right] \leq 2 \cdot \exp \left( -2 \epsilon^2 N \right)
\tag{ $6$}
$$
同样的，当 $\epsilon$一定（一般都很小），并且训练样本 $N$足够大的情况下，我们有 $E_{in} \approx E_{out}$，也就是说 $g(x) \approx f(x)$，这时候的流程图就变成了一个 $h$对应一个 $f$的情况了，如图五所示。

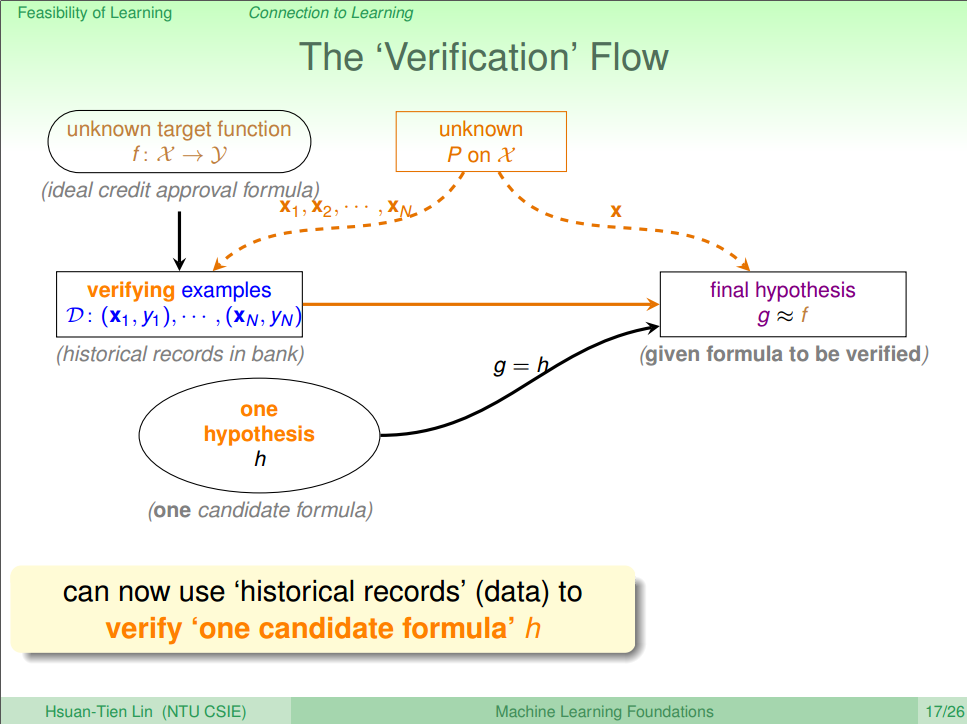
图五 A Verification Flow ^[3]

但这个并非是真正意义上的学习，因为只有一个Hypothesis(因为通过一个一段数据集，我们只能得到一个Hypothesis)，所以我们下面讨论多个。

3) Connection Between Hoeffding Inequity and Real Learning

上面我们讨论了根据Hoeffding Inequity，在 $N$无限大的时候，一个Hypothesis的 $\lvert E_{in} - E_{out} \rvert < \epsilon$的概率会无限的小，所以同时满足 $\epsilon$ 很小 且 $N$很大的情况下，我们可以得到 $E_{in} \approx E_{out}$。

疑问：但是在应对多个Hypothesis的时候，我们就有多个 $h(x)$ 和多个 $E_{in}$，那样我们真的能确定 $E_{in} \approx E_{out}$ 吗？

① Introduction of Bad Data

在连续抛5次硬币过程中，一个人抛到正面朝上的概率为 $\frac{1}{32}$，如果现在有150个人，那么这150个人里面，至少有一个人5次都抛出正面朝上的几率为 $1- (\frac{31}{32})^{150} > 99\%$。

分析： 因为一个人连续5次抛出正面朝上几率为 $\frac{1}{32} < 3\%$， 所以如果机器学习的话，在测试的时候他更偏向于预测“不能连续抛出5次正面朝上”（因为选择会偏向于选择概率更大的一边）。但是当150次试验的时候，一个人连续5次抛出正面朝上的几率 $E_{out}>99\%$，而在训练的时候的概率$E_{in} < 3\%$，也就是说机器学习了之后进行了错误的估计（即$E_{in} 远远\neq E_{out}$。导致这种结果的几率就是所谓的 bad data（也就是Noise:偏差值，数据与所需数据不吻合等）。

疑问：

1.如果说存在bad data，那样的话怎么区分呢？（下面会证明bad data出现的概率）。

2.如果万一 $E_{in}$ 很大的话，那么 $E_{out}$ 也很大，那么这机器学习还什么意义呢？(这个问题后面解释)

② Probability of Bad Data

首先在单个假设的时候如图六所示

图六 Bad Data for One h ^[4]

而在多个假设的时候如图七所示

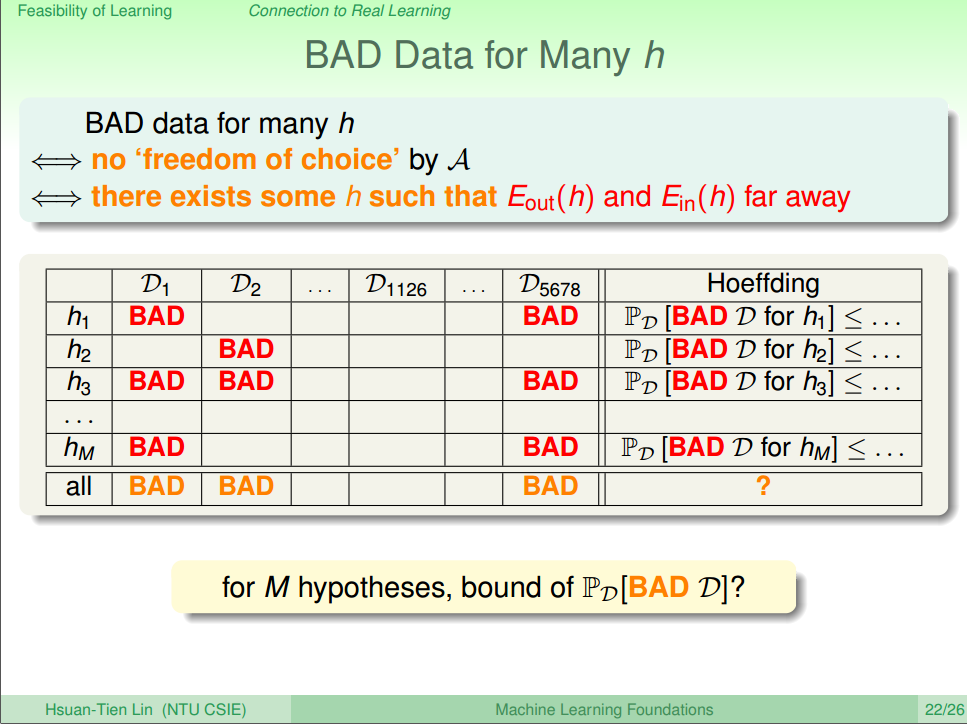
图七 Bad Data for Many h ^[4]

最后计算 Bad Data发生的概率如图8所示。

图八 Bound of Bad Data ^[4]

由计算结果可以发现，这里的M是一个有限的数，所以当训练样本 $N$ 越大，那么Bad Data出现的概率越低，$E_{in} \approx E_{out}$；如果训练样本 $N$一定的情况下，M越大，也就是说Hypothesis越多，那样可以供我们用算法 $A$进行选择的越多，那么越有可能选到一个好的样本，使得 $E_{in} \approx 0$

总结如下表：

-	M很小的时候	M很大的时候	N很小的时候	N很大的时候
$E_{in}(g) \approx E_{out}(g)$	Yes，Bad Data的数量也少了	No，Bad Data的数量也多了	Yes，Bad Data出现的概率变小了	No，Bad Data出现的概率变大了
$E_{in}(g) \approx 0$	No，选到低错误率的可能性变小了	Yes，选到低错误率的可能性变大了	没必然联系，样本总数多于少，与错误率无关	没必然联系，样本总数多于少，与错误率无关

最终我们的Learning Flow 就可以变成图9。

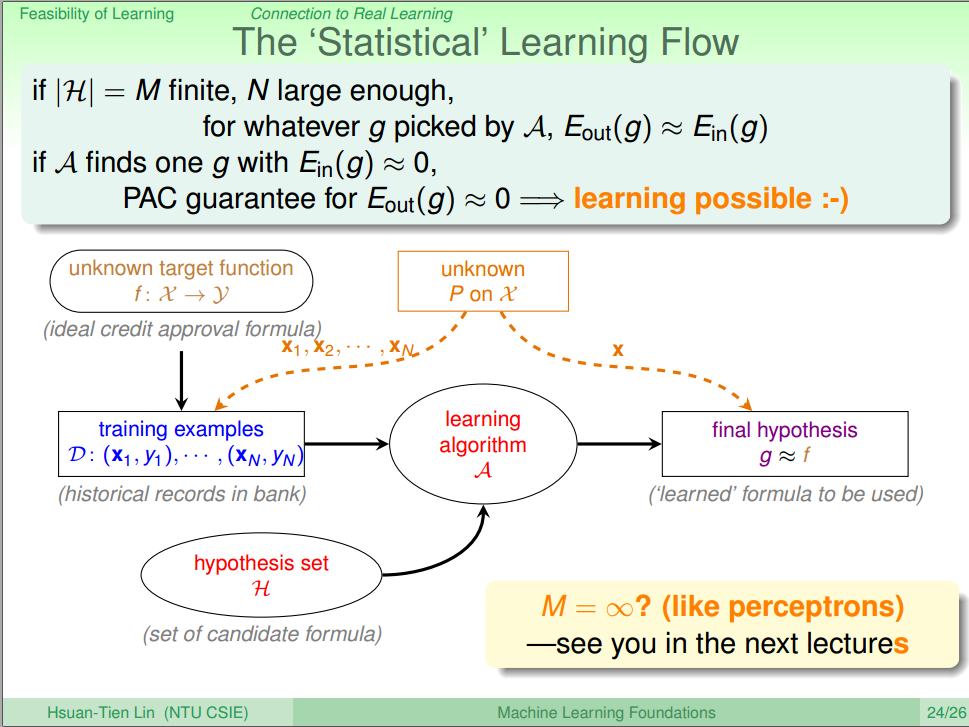
图九 The Statistic Learning Flow ^[4]

在足够样本的情况下，机器算是能学到东西了!

---

Summary

这章主要讨论 Whether machine learning is possible or not.
思路：
1. 首先直线学习是不可能的：因为输入样本与实际测试样本差别可能很大
2. 1中讨论的情况是事情，但是有根据统计学中的Hoeffding不等式，可以有补救的办法（某种程度上，可以使得学习后的机器在实际测试中有较小的错误），然后根据Hoeffding不等式，来联系机器学习，说明机器学习是某种程度上可行的

---

Reference

1.机器学习基石(台湾大学-林轩田)\4\4 - 1 - Learning is Impossible- (13-32)

2.机器学习基石(台湾大学-林轩田)\4\4 - 2 - Probability to the Rescue (11-33)

3.机器学习基石(台湾大学-林轩田)\4\4 - 3 - Connection to Learning (16-46)

4.机器学习基石(台湾大学-林轩田)\4\4 - 4 - Connection to Real Learning (18-06)