KMP算法(详解+图解 BF算法 next数组的优化问题 字符串匹配问题 c语言实现)

1.什么是KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) ----百度

应该是通过next[]数组实现

2.使用场景

char str1[]="abcdacbdef"
char str2[]="abcd"

在str1中寻找子串str2，并返回一个数字。
该数字为从主串第几个字符开始找到子串。

在说KMP算法的时候，我们先了解一下暴力求解

3.暴力求解法

暴力求解法的基本思路：
1.两个指针s1,s2分别指向str1,str2，通过s1,s2遍历数组。
2.在对应字符相同的情况下，s1,s2后移。
3.不相同的情况下，s1,s2需要回退到某个位置，重新匹配。
4.s2回退的位置很容易，就是str2,但是s1每次找到相同的字符，s1偏移后，指向已经改变了，我们需要在设置一个指针指向偏移后的起始位置。

C语言两种实现方式

#include<stdio.h>
#include<assert.h>
#include<string.h>
int ForceSearch(char* str1, char* str2)
{assert(str1 && str2);//断言，两个指针不能为空，为空报错//指针形式char* s1 = str1;//遍历搜寻char* s2 = str2;//遍历搜寻char* p = str1;//记录偏移后的起始位置while (*p){s1 = p;//回退到str1当前的起始位置s2 = str2;//回退到str2起始位置//*s2 !='\0' 必须得有//如果*s1 == *s2 == '\0'那么会出错while (*s1 == *s2 && *s2 != '\0'){s1++;s2++;}//找到if (*s2 == '\0'){return p - str1;//返回下标}//未找到p++;}//遍历完未找到return -1;//数组形式/*int i = 0;int j = 0;int p = 0;//记录主串的起始位置int len1 = strlen(str1);	int len2 = strlen(str2);//i，j自增是有条件的，必须相同的时候，所以不要用for循环//非得用for的时候自增不写在()内部while (i < len1 && j < len2){i = p;j = 0;//相同的情况下while (str1[i] == str2[j] && str2[j]!= '\0'){i++;j++;}//不相同的情况下2中情况if (str2[j] == '\0'){return p;}p++;}	//找不到返回-1return -1;*/
}int main()
{printf("%d\n", ForceSearch("aabbcde", "bcd"));printf("%d\n", ForceSearch("aabbcde", "cde"));printf("%d\n", ForceSearch("aabbcde", "ab"));return 0;
}

注意这里的地址，下标都是从0开始的

数组和指针访问的方式是打通的，不了解的可以看这里
盘复数组与指针的那些知识

4.KMP算法

暴力求解法，i,j每次都是需要回退，如果字符串特别长，那耗费的时间会很多。
KMP算法能够很好解决回退的问题。

KMP算法的核心思想是： i(i表示:i变量遍历主串str1)不回退，j（j表示:j变量遍历子串str2）回退到特定的位置。

next数组内部的元素就是这个特定位置的下标。
str2中的每个字符都会有一个特定的回退下标。

4.1求next数组中元素

4.11给定一组子串(str2)和next数组并对其解释

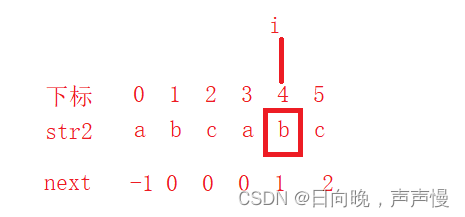
比如说
当i下标为3时，子串与主串匹配不成功，子串回退到下标为0处，重新与主串匹配
当i下标为4时，子串与主串匹配不成功，子串回退到下标为1处，重新与主串匹配

4.12next数组元素的查找方式

next数组中的元素(是回退值，也是回退下标，下文有多次出现，提前说清)，是真子串的长度。
什么是真子串呢？真子串是在str2中出现的字符串。
是什么样的真子串呢？必须是以str2[0]开头，以str2[i-1]结尾。(一定是以下标为0开始)
这样的真子串需要找到两个，存在，那么对应nenxt[i]就是真子串的长度

通过下面两张图来理解

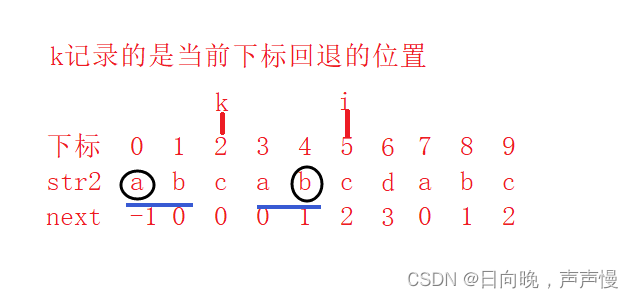
str2[0]–>a ，str2[i-1]–>b ，以a开头，以b结尾。并且存在两个这样的真子串，那么next[i]就是真子串的长度，即next[5]=2。

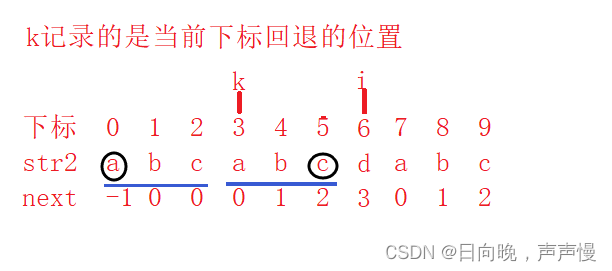
你们可能会问为什么next[0]=-1。人为设置的，你也可以设置其他值，不过设置-1的时候用起来更加的方便。

根据上面那个图，假设题目是求str2的next数组（选择题），你已经求出来了，是以next[0]=-1的next数组， 但是选项中给你的next数组是以next[0] = 1开始 的。你就将你求的next数组，内部元素+1就可以找到答案了。

我们也需要能够发现，如果下标i处与下标i-1处，都能找到真子串的话，他们回退的下标差是1。
换句话说，每次增加的都是以1递增。
所以每次找下一个退回值的时候（next[i+1]），我们可以在之前一个的基础上增加1（next[i]+1），看是否能找到。

比如，找下标6的，看next[5]=2，那就+1（2+1=3），看看是否存在长度为3的两个真子串。找到了就写3，找不到另说。

如何使用程序语言来描述呢？

我们可以知道的是next[0]=-1,next[1]=0。(头两个字符肯定找不到两个真子串，直接设好)那初始化的时候，可以设，k=0,i=2。开始遍历。
那如何求next[i]呢？
比如下面这张图，注意k的含义。

在此之前我们得先简单推导一下公式（这里注意好i,k的含义）

4.13推导公式

已经知道了真子串是以str2[0]开始，以str2[i-1]结尾
那我换种写法 str2[0]…str2[k-1] == str2[x]…str2[i-1]。x是未知数。
为什么是k-1，很好理解，k表示的是回退值，也是是真子串的长度也就是有k个字符。
因为是从0开始所以得-1。
比如 0-2 有3个数（0，1，2）
i表示当前下标，k记录当前下标的回退值

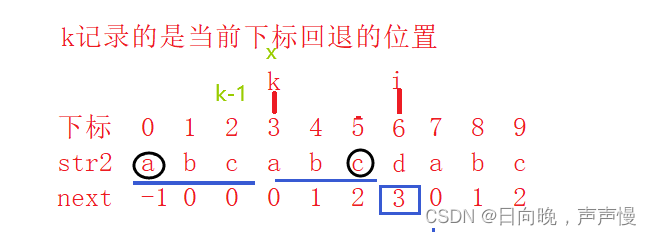
通过这两张图片相信能理解我所表达的含义了。
str2[0]…str2[k-1] == str2[x]…str2[i-1]
两边长度相等所以可以得到：
k-1-0=i-1-x
x=i-k。
即
str2[0]…str2[k-1] == str2[i-k]…str2[i-1]

现在要求的是next[i+1] = ?

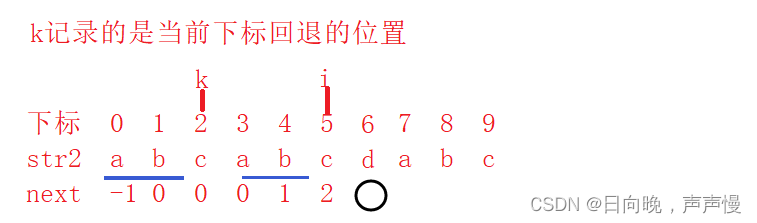
看下面这张图，next[i+1]=3为什么呢？是因为 str2[i]=str2[k]
结合上面所说的去理解一下：知道每次增加都是以1递增，那找回退值时，可以这样。比如求next[i+1]，找前面一个next[i]先next[i]+1，看看能否找到长度为next[i]+1的真子串。找到了，那么next[i+1] = next[i]+1。这里+1的1其实就是str2[i]=str2[k]相同的情况下。不相同那情况是不一样的

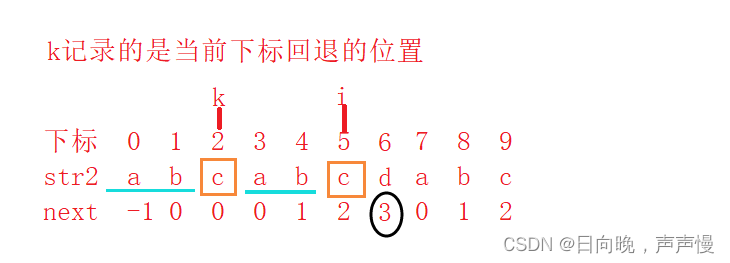
铺垫工作做完了那我们开始推理一下公式.
再次回顾下，k是当前下标的回退值（回退下标）也就是真子串的长度

当下标i，存在回退值(不为0)，可以得到 str2[0]…str2[k-1] == str2[i-k]…str2[i-1] （长度即为k）

假设当前下标i和当前下标i所对应的回退值k匹配成功
即 str2[i]==str2[k]
是不是就可以得到 --> str2[0]…str2[k-1] str2[k] == str2[i-k]…str2[i-1] str2[i]

这两个真子串的长度 （k+1）不是就是下一个坐标（i+1）的回退值嘛，即 next[i+1]
那么是不是也可以得到 next[i+1] = k+1

看下面的图理解一下

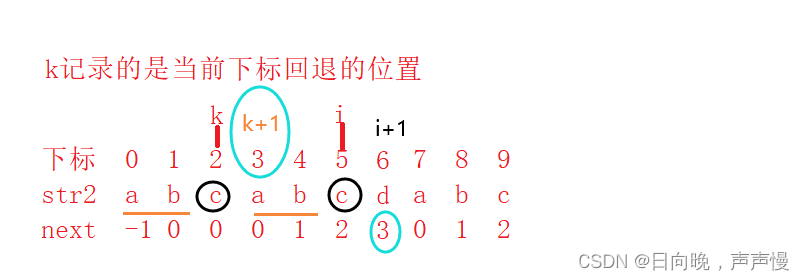
推导公式最终是要得到的是 如果 str2[i] 等于 str2[k] 可以得到 next[i+1] = k+1
注意这个时候的k是当前下标的回退值。下面说的时候k的含义不同了，不要绕晕了。

4.14求当前的next[i]。

上面已经说了，i，k在初始化的时候分别为2，0。这是因为next[0]=-1,next[1]=0，这两个先规定好。原因也很简单头两个字符肯定是找不到两个真子串的！
现在要求next[i]

上面这个图片的例子直接讲可能不太好理解我们换一张图

再次提醒k 是前一个下标的回退值

①匹配成功的情况

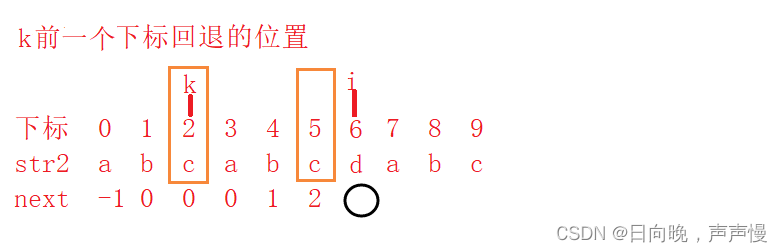
匹配成功，这个时候的条件是 str2[i-1] 等于 str2[k] 得到 next[i] = k + 1

再次说下，注意k的含义，因为k的含义不同，k是前一个下标（i-1）的回退值，所以这里是i。之前的讲的时候，k是当前下标的回退值，得到next[j+1]=k+1。(为了区分用j说明)和这里是不矛盾的

这里求i下标处的回退值，k是i-1处的回退值
上面求j+1下标处的回退值，k是j处的回退值
next[]，[]中的下标和 k所对应的下标差值始终是1。

在回过头来看下面一张图

因为 str2[i-1] == str2[k] --> next[i] = 1 -->next[2] = 1

②匹配不成功的情况

下面图是特殊情况先等下说

看下面这张图

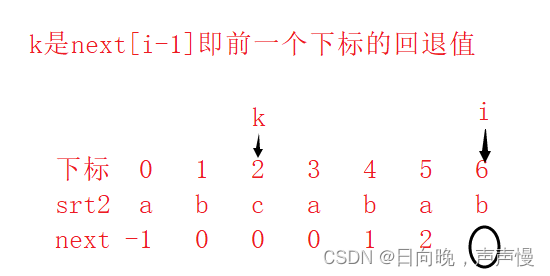
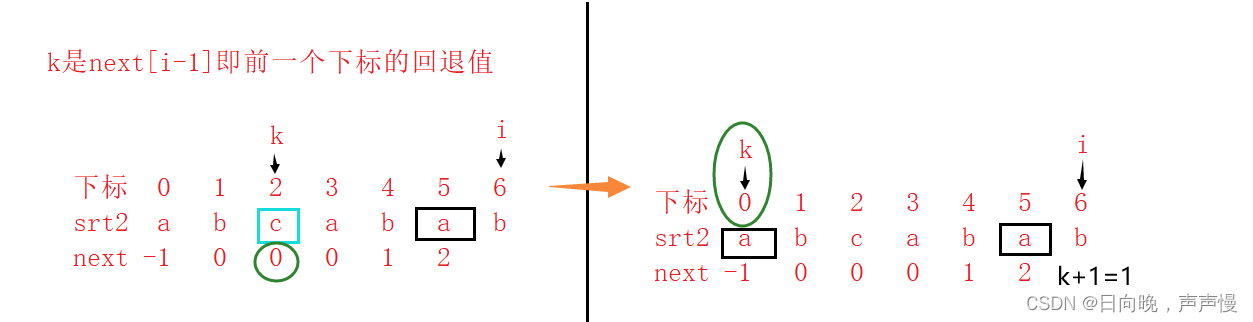
先说明在解释：当第一次匹配不成功的时候，k要继续回退，回退到哪呢？回退到next[k]处（当前k所在下标处的回退值），继续重新匹配。
看是否能够匹配成功，成功的话 next[i] = k+1;
不成功继续回退

直到k回退到-1的时候就不会在回退了。
比如下面这个例子

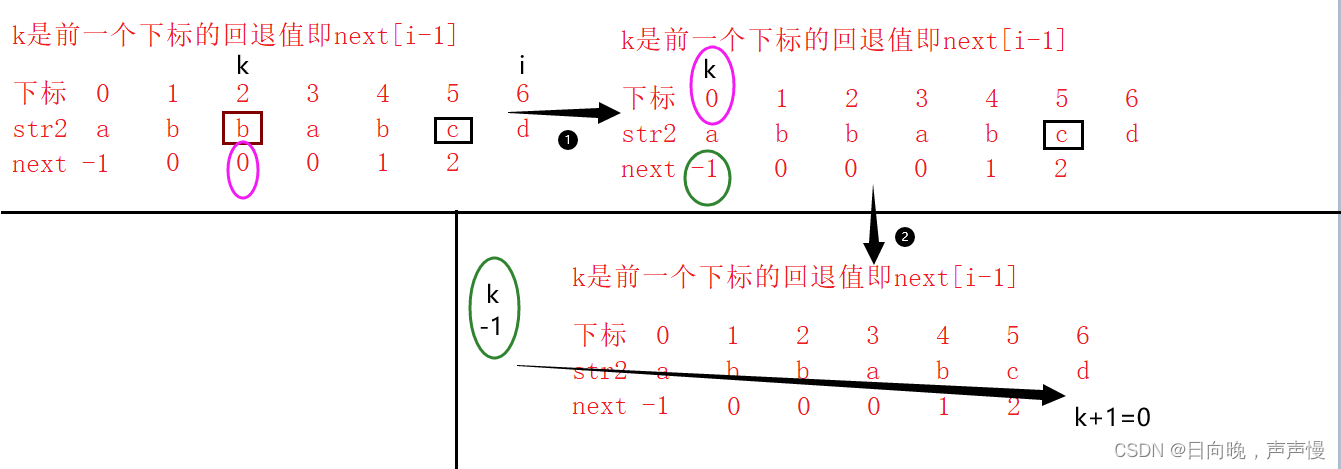
这个时候刚开始的那张图就很好理解了

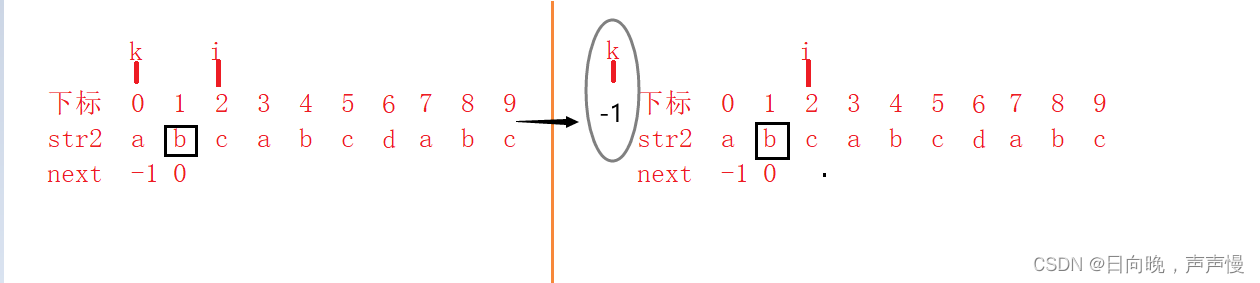
有人会问当k==-1的时候，为什么next[i]能够等于 0 ，之前有说过，退回的下标递增时差值是1，
只要我们把k==-1这个条件，设置好，就可以和递增差值为1，统一起来了。
这时候在看我们设置的next[0]=-1，next[1]=0 是不是和递增差值为1匹配起来了，这就是设置为-1的好处。

以上就是KMP的核心思想。

5.C语言实现KMP算法

#include<stdio.h>
#include<assert.h>
#include<string.h>
#include<stdlib.h>
void GetNext(int* next, char* str2, int len2)
{next[0] = -1;next[1] = 0;int i = 2;//当前下标int k = 0;//前一个回退下标  //这里i递增是有条件限制的，匹配成功的时候才能递增。//所以不用for，非要用自增不能写在（）内。while (i < len2){if (str2[i-1] == str2[k]|| (k == -1))//这里就是我所说的将k==-1 和 递增的差值1统一起来{next[i] = k + 1;k++;i++;}else{k = next[k];}}
}int KMP(char* str1, char* str2)
{assert(str1 && str2);//断言，两个指针不能为空，为空报错int len1 = strlen(str1);int len2 = strlen(str2);int i = 0;int j = 0;int* next = (int*)malloc(sizeof(int) * len2);//得到next数组的元素GetNext(next, str2, len2);//i不需要回退并且i不是一直自增，需要在对应字符相同的条件下在自增//千万别用了for循环，当然要是你非得用也是可以的，只要自增不写在（）里就可以。while(i<len1 && j<len2){if (j == -1 || str1[i] == str2[j])//这里写的时候不能忘记j==-1的情况，第一个就没匹配成功的时候,j=0,next[0]=-1{//对比暴力求解 并分析//因为这是if语句，只执行一次，两者是不可能为'\0'进入if条件的。//如果是while语句这样写就需要斟酌一二了。i++;j++;}else{//匹配不成功，让j回退到特定的位置j = next[j];}}if (str2[j] == '\0'){//这里是返回起始地址。//别问我为什么这样，你自己动笔笔画几下就能发现了。return i - j;}return -1;}
int main()
{printf("%d\n", KMP("aabbcde", "bcd"));printf("%d\n", KMP("aabbcde", "cde"));printf("%d\n", KMP("aabbcde", "ab"));return 0;
}

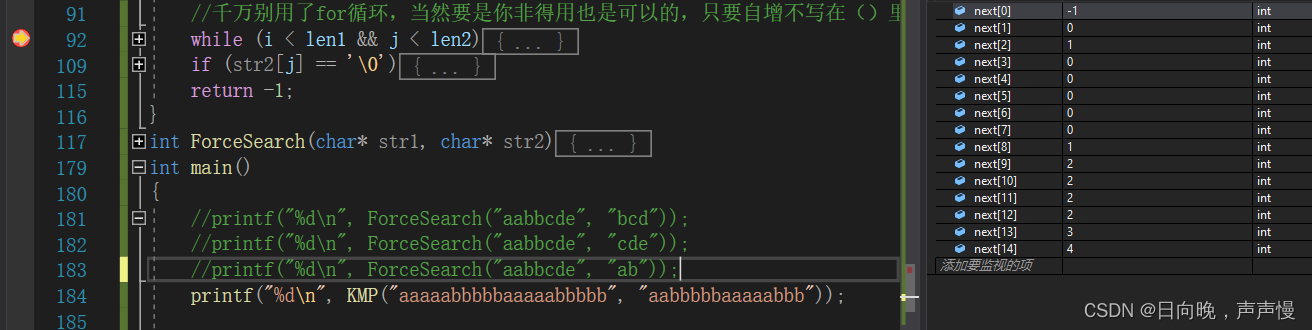
再次说明，是从0开始计算的。

6.补充说明

看下图，大家是不是觉得和上述说的，每次递增+1违背呢？
其实并没有。我们需要知道每次递增+1的前提条件是，在匹配成功下才递增+1。
举例：
当要计算next[10]的时候，第一步：str2[9]和str2[2]匹配，不成功，回退。回退到下标2处（k=2），str2[2]和str2[9]匹配不成功，继续回退，回退到下标为1处(k=1)，str2[1]和str2[9]匹配成功，则next[10]=k+1=2。所以和每次递增+1是不违背的。

例如下图所示

7.应用拓展

请你分别使用暴力求解，和KMP算法实现strstr()。

主串是 string,子串是strCharSet，从主串找子串，找到返回主串中对应的起始地址。找不到返回NULL

strstr的模拟实现

8. 关于next数组的优化问题

来看下图

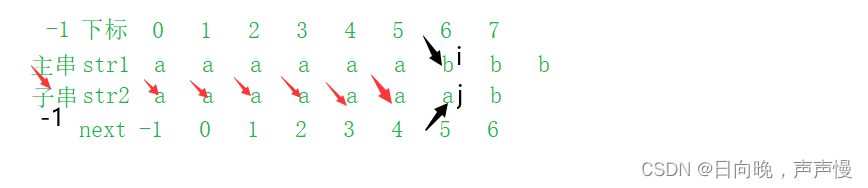
如果当i=6的时候，与主串匹配不成功的话，是不是需要跳转多次才能到达最终位置（下标为-1处）。这过程就存在一定时间浪费，如果我们可以直接回退到-1处，这样回退的时间会更短。这也就是我们next数组的优化。

那什么时候回退呢？

比如说，i = 6的时候，回退到i=5，对应的字符相同，那next[6]=next[5]。
你可能会问不是说回退到-1嘛，这样写不就是回退到5了嘛？？？
那是因为，前面回退值还没有改动。计算的时候，肯定是先把前面的回退值计算出来，我们应该是从下标为1处开始优化。
回退处的字符与当前下标处的字符相同的时候，当前下标的回退值，就是回退处的回退值就拿刚才的例子再说一次，回退处（i=5）字符是a，当前下标（i=6）的字符是a它们相同，那么当前下标的回退值（next[6]）就是回退处（i=5）的回退值（next[5]），即next[6]=next[5]

如果不相同的话，我们需要回退嘛？当然不需要，保存原有的值即可。

怎么实现呢？也很容易，在原有的基础上稍作修改。
首先，不在从下标为2处开始，而是从下标1处开始，添加新条件，回退处的字符与当前下标处的字符相同的时候，当前下标的回退值，就是回退处的回退值

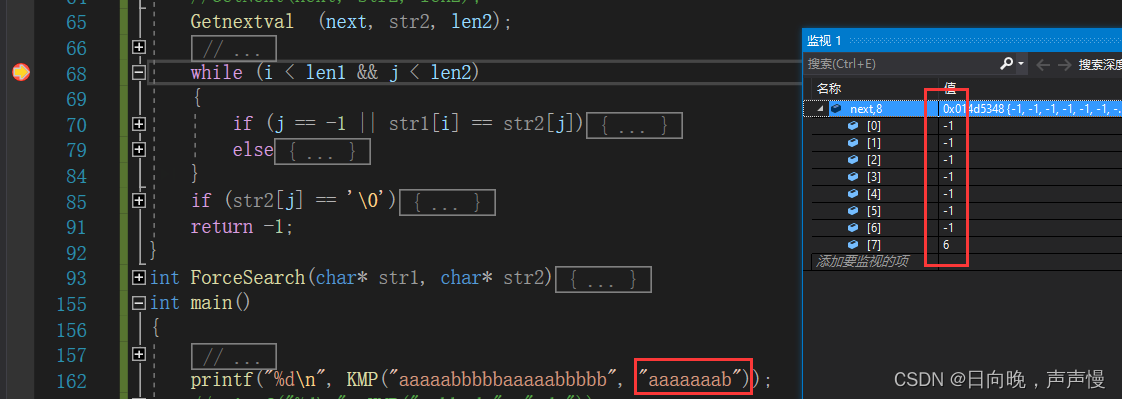
void Getnextval(int* next, char* str2, int len2)
{assert(next && str2);int k = -1;//前一个下标的回退值int i = 1;//改动处next[0] = -1;next[1] = 0;while (i < len2){if (k == -1 || str2[k] == str2[i - 1]){next[i] = k + 1;if (str2[i] == str2[next[i]])//改动处next[i] = next[next[i]];k++;i++;}else{k = next[k];}}
}

子串：abcaabbcabcaabdab也可以手动算算在对比下结果

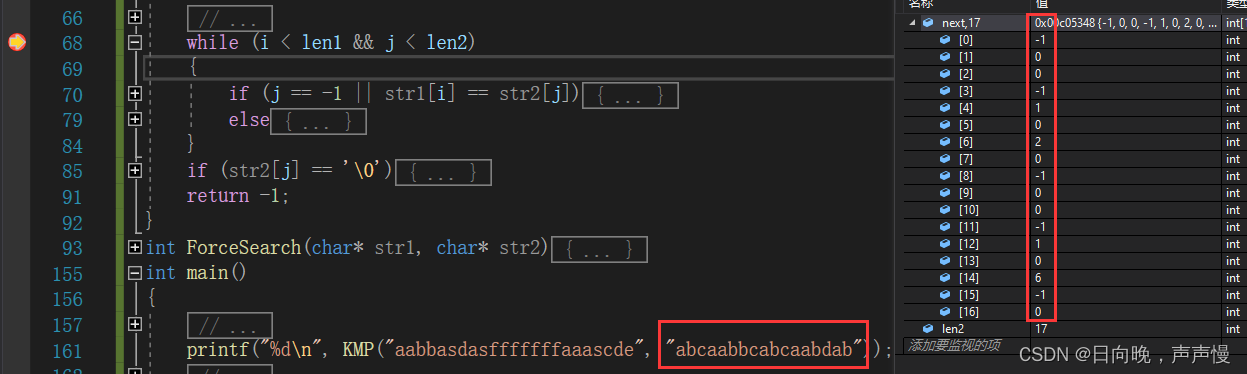
同样的我们的nextval是从next[0]=-1开始的，如果题目是以next[0]=1开始，只要把我们所求的next数组中的元素+1即可

9.小结

KMP算法的核心就是求next数组。

记住结论
i是当前下标，k=next[i-1]即前一个下标的回退值
当str2[i-1]==str2[k] --> next[i] = k+1
当str2[i-1] != str2[k] -->k = next[k] -->重新匹配…k=-1。
匹配不成功的时候，k跳转，再匹配，重复这个动作，直到k=-1结束跳转。

next数组的优化
从下标1开始
添加新条件回退处的字符与当前下标处的字符相同的时候，当前下标的回退值，就是回退处的回退值。