通过雷诺方程运用matlab求解滑靴底部油膜厚度场、压力场、剪切场及速度场

2024-01-20 10:10
文章标签 matlab 方程 底部 速度 求解 运用 压力 剪切 厚度 雷诺 滑靴 场及 油膜

本文主要是介绍通过雷诺方程运用matlab求解滑靴底部油膜厚度场、压力场、剪切场及速度场，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

通过matlab建立程序求解滑靴底部密封面的压力场、剪切场及速度场

1 滑靴油膜压力场方程的建立
在圆柱坐标系下的累诺方程为：
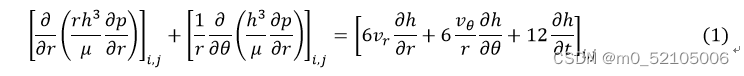
在这里插入图片描述
利用五点差分法将两项展开成差分形式为：
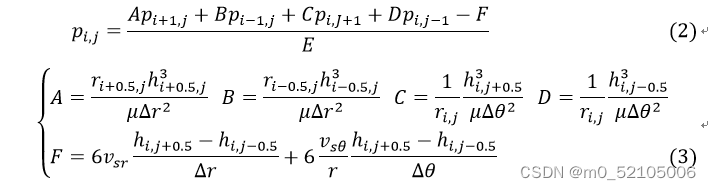
h——油膜厚度；p——油膜压力；μ——动力粘度；v_sr——油膜径向剪切速度；v_sθ——油膜周向剪切速度。在这里插入图片描述
通过中心油膜厚度来计算油膜的厚度场为：
中：h_c为中心油膜厚度，h_c=10μm；∂滑靴倾斜角度, ∂=0.00075rad。
边界条件设置：设置滑靴油室到密封面角接触处的压强设置为入口压力，滑靴外径处与外界的交界面设置为出口压力。这里的入口压力设置为35Mpa，出口压力为0.2Mpa。将网格划分为20×50。径向m=20，周向n=50。根据粘性流体流动的特性，设置密封面处油膜顶部的速度为初速度，最底部的速度为0，即：
在这里插入图片描述采用超松弛迭代法进行求解，求解的方法是对线性方程组进行迭代求解，迭代收敛的依据为：
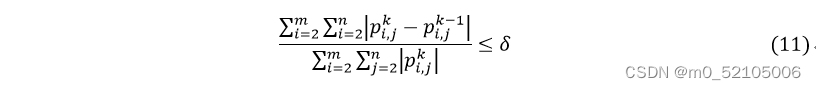
当油膜压力连续迭代误差小于δ=〖10〗^(-10)时迭代停止。
通过如下mtlab代码实现：

%%%%利用松弛迭代法求解差分方程如下。
%清除命令窗口及工作区变量
clc
clear
%定义网格数量，a表示径向，b表示周向；
a=20;b=50;                            
%定义主要参数，ww为缸体转速，hc表示中心油膜厚度，hc=10um,miu表示动力粘度;
dR=1/a;dT=1/b;ww=4000;hc=10*10^-6;miu=0.041; 
%定义微分区间的大小，并设置边界条件为入口35Mpa,出口1MPa;
dertaR=2/a*10^-3;dertaT=1/b*2*pi; ps=3.5*10^7;pc=2*10^5;    
%滑靴外径4mm,内径2mm,滑靴倾角0.00075rad,任意角度滑靴油膜厚度为c;
Rs=4*10^-3;Ri=2*10^-3;alpha=0.00075;c=hc+Rs*tan(alpha);
%计算滑靴的径向速度ur和周向速度uc;
ur=ww*2*pi/50*9.5*10^-3*cos(12/180*pi);uc=ww*2*pi/50*9.5*10^-3*sin(12/180*pi);
%定义边界节点的压力为0，这是为了方便计算;t矩阵为了后边方便储存数据；
p(a,b)=0;t=[];
%定义后面迭代的矩阵大小，由于迭代的需要，将矩阵两个方向的维度均增大1；
a1=a+1;b1=b+1;a2=a-1;b2=b-1;
A=zeros(a1,b1);B=zeros(a1,b1);C=zeros(a1,b1);D=zeros(a1,b1);
E=zeros(a1,b1);F=zeros(a1,b1);G=zeros(a1,b1);
%定义边界节点的压力为0.2Mpa，这是为了方便计算；
p(a1,b1)=200000;
%计算滑靴油室的压力，
ld1=8e-4;l1=5.4e-3;
ld2=6e-4;l2=2.1e-3;
q1=1.53e-8;  %柱塞排量，
p2=ps-(q1*128*miu*l1)/(pi*(ld1)^4)-(q1*128*miu*l2)/(pi*(ld2)^4)t1=clock;
%设置入口压强为35Mpa,出口压强为0.2Mpa;
for j=1:b1p(a1,j)=pc;
end
for j=1:b1     %定义底边的边界条件压力为0p(1,j)=ps;
end%以下循环语句是根据雷诺方程变化成差分形式，对差分式各项系数矩阵ABCDEF进行求解；
for j=2:bj1=j-1;j2=j+1;j11=2*(j-1)-1;j12=2*j-1;for i=2:ai1=i-1;i2=i+1;i11=2*(i-1)-1;i12=2*i-1;T=dT*j*2*pi;R=2*10^-3+dertaR*i;H=hc-R*tan(alpha)*cos(T);HHH(i,j)=hc-R*tan(alpha)*cos(T);dhdr=-tan(alpha)*cos(T);dhdt=R*tan(alpha)*sin(T);dhdr1(i,j)=dhdr;dhdt1(i,j)=dhdt;if j==50&&i==20    %边界条件使得接口处的偏导数相同dhdt1(:,50)=dhdt1(:,1);endT1=dT/2*j11*2*pi;T2=dT/2*j12*2*pi;R1=2*10^-3+dertaR/2*10^-3*i11;H1=hc-R1*tan(alpha)*cos(T);R2=2*10^-3+dertaR/2*10^-3*i12;H2=hc-R2*tan(alpha)*cos(T);H3=hc-R*tan(alpha)*cos(T2);H4=hc-R*tan(alpha)*cos(T1);if j==50&&i==20    %边界条件使得接口处的偏导数相同dhdt1(:,50)=dhdt1(:,1);endA(i,j)=R2*H2^3/(miu*dertaR^2);B(i,j)=R1*H1^3/(miu*dertaR^2);C(i,j)=H3^3/(R*miu*dertaT^2);D(i,j)=H4^3/(R*miu*dertaT^2);E(i,j)=A(i,j)+B(i,j)+C(i,j)+D(i,j);F(i,j)=6*miu*ur*dhdr1(i,j)+6*miu*uc*dhdt1(i,j);end
end
HHH=HHH(2:a,2:b);%设置初始误差和迭代数为1；error=1;N=1;
%设置循环语句，当满足精度条件error<=1e-10时结束循环；
%采用线性方程组的迭代求法对差分方程进行求解，并将结果放在p矩阵中while error>=1*10^-6p1=p;for j=2:bj1=j-1;j2=j+1;for i=2:ai1=i-1;i2=i+1;p(i,j)=(A(i,j)*p(i2,j)+B(i,j)*p(i1,j)+C(i,j)*p(i,j2)+D(i,j)*p(i,j1)-F(i,j))/E(i,j);endendHE=mean(p1(:));HG=mean(p(:));error=abs((HE-HG)/HG);N=N+1;end
%对迭代得到的矩阵进行处理（去掉周向上为0的边界条件）方便得到较好的数据和图像;
pr=p;
prr=pr;
prr(:,1)=pr(:,2);
prr(:,b1)=pr(:,a1);
p1=p(1:a,2:b);%下面根据已有的压强场求解速度场分布
H=hc-R*tan(alpha)*cos(T);
Hm=hc-R*tan(alpha)*cos(pi);
Hm=hc;
for j=2:bjj1=j-1;jj2=j+1;for i=2:aii1=i-1;ii2=i+1;R=2*10^-3+dertaR*i;c=a;dertaz=hc/a;HH=linspace(0,hc,20);ha=15;dpdr(i,j)=(prr(ii1,j)-prr(ii2,j))/(2*dertaR);dpdt(i,j)=(prr(i,jj2)-prr(i,jj1))/(2*dertaT);vr(i,j)=-1/(2*miu)*dpdr(i,j)*(HH(ha)^2-HH(ha)*Hm)+ur*HH(ha)/Hm;vt(i,j)=-1/(2*miu)*dpdt(i,j)*(HH(ha)^2-HH(ha)*Hm)+uc*HH(ha)/Hm;vreal(i,j)=sqrt(vr(i,j)^2+vt(i,j)^2);taor(i,j)=dpdr(i,j)*Hm/2+miu*ur/Hm;taot(i,j)=dpdt(i,j)*Hm/(2*R)+miu*uc/Hm;tao(i,j)=sqrt(taor(i,j)^2+taot(i,j)^2);fs1(i,j)=(vr(i,j)*taor(i,j)+vt(i,j)*taot(i,j))*2*pi*R*dertaR*dertaT;ws2(i,j)=vr(i,j)*Rs*dertaz;end
end
fs1;
fsz=sum(fs1(:));for j=2:bHm=hc;jj3=j-1;jj4=j+1;for i=2:aii3=i-1;ii4=i+1;R=2*10^-3+dertaR*i;dertaz=hc/c;HH=linspace(0,hc,c);%设定滑靴速度变化主要由径向变化导致，周向上设置不变;dpdr(i,j)=(prr(ii3,j)-prr(ii4,j))/(2*dertaR); 
%用t矩阵储存计算得到的速度矩阵vreal;
t=[];k=1;
%计算滑靴底部的速度场vrr;
while k<=cfor j=2:bfor i=2:avr(i,j)=-1/(2*miu)*dpdr(i,j)*(HH(k)^2-HH(k)*Hm)+ur*HH(k)/Hm;vt(i,j)=-1/(2*miu)*dpdt(i,j)*(HH(k)^2-HH(k)*Hm)+uc*HH(k)/Hm;%计算粘性摩擦功损失fs1以及滑靴外径处的泄漏量ws2;vreal(i,j)=sqrt(vr(i,j)^2+vt(i,j)^2);            endendt=[t,vreal];k=k+1;
endfor k=1:aLL=(k-1)*b+1;LS=k*b;vrr(k,:)=t(a,LL:LS); %这部分的目的在于获得不同厚度下的速度;endend
end%去掉第一行第一列的0项得到较贴切的速度矩阵;
vrr1=vrr(2:a,2:b)/5;dertaT1=1/b*2*pi;dertaH=hc/(c-1);Q=vrr1*dertaT1*dertaH;Q1=sum(Q(:));Q2=Q1*60/1000;                      %计算泄漏量wxL=Q2*(ps-pc);                     %泄露能量损失fsz;                                %粘性摩擦功损失wt=wxL+fsz;                         %总的能量损失taoavge=sum(tao(2:a,2:b));paverage=sum(pr(2:a,2:b));taoavge1=sum(taoavge(:))/(a2*b2);   %切应力平均值paverage1=sum(paverage(:))/(a2*b2); %压强平均值miuu=taoavge1/paverage1;            %摩擦系数Fmi=paverage1*pi*(Rs^2-Ri^2);       %密封面支承力;Fz=Fmi+p2*pi*Ri^2;                  %总支承力;t2=clock;tzong=etime(t2,t1);e1=['迭代次数为：',num2str(N)];e2=['迭代精度为：',num2str(error)];e3=['程序计算时间为：',num2str(tzong)];e4=['输出的主要参数为：'];e5=['平均压强值为：',num2str(paverage1)];e6=['切应力平均值为：',num2str(taoavge1)];e7=['摩擦系数为：',num2str(miuu)];e8=['泄漏量为：',num2str(Q1)];e9=['泄漏量能量损失：',num2str(wxL)];e10=['粘性摩擦功为：',num2str(fsz)];e11=['总能量损失为：',num2str(wt)];e12=['密封面静压力为：',num2str(Fmi)];e13=['总静压力为：',num2str(Fz)];%显示主要输出参数disp(e1)disp(e2)disp(e3)disp(e4)disp(e5)disp(e6)disp(e7)disp(e8)disp(e9)disp(e10)disp(e11)disp(e12)disp(e13)%%%下面绘制主要图像
%绘制滑靴底部油膜厚度场
r1=linspace(0.2,0.4,a2);
t1=linspace(0,2*pi,b2);
x1=zeros(a2,b2);
y1=zeros(a2,b2);
for i=1:a2x1(i,:)=r1(i)*cos(t1);y1(i,:)=r1(i)*sin(t1);
end
figure(1)
HHH=HHH*1e6;%将厚度单位转化为um；
pt1=surf(x1,y1,HHH);%绘制滑靴底部的厚度场图
set(pt1,'edgecolor','none') %如果网格数量太多可加上，方便查看结果;
title('滑靴底部油膜厚度场','FontSize',15,'FontWeight','bold','Color','r')
xlabel('r/mm','FontSize',15,'FontWeight','bold')
ylabel('r/mm','FontSize',15,'FontWeight','bold')
zlabel('h/um','FontSize',15,'FontWeight','bold')
colorbar
colormap("jet")
view(-90,90)%绘制滑靴底部压力场
r1=linspace(0.2,0.4,a);
t1=linspace(0,2*pi,b2);
x1=zeros(a,b2);
y1=zeros(a,b2);
% p1=p(1:a,2:b);
for i=1:ax1(i,:)=r1(i)*cos(t1);y1(i,:)=r1(i)*sin(t1);
end
figure(2)
pt2=surf(x1,y1,p1);%绘制滑靴底部的压力场
set(pt2,'edgecolor','none')   
title('滑靴底部油膜压力场','FontSize',15,'FontWeight','bold','Color','r')
xlabel('r/mm','FontSize',15,'FontWeight','bold')
ylabel('r/mm','FontSize',15,'FontWeight','bold')
zlabel('压强/pa','FontSize',15,'FontWeight','bold')
colorbar
colormap("jet")
view(-40,40)%绘制滑靴底部剪切压力场
r2=linspace(0.2,0.4,a2);
t2=linspace(0,2*pi,b2);
x2=zeros(a2,b2);
y2=zeros(a2,b2);
tao1=tao(2:a,2:b);
for i=1:a2x2(i,:)=r2(i)*cos(t2);y2(i,:)=r2(i)*sin(t2);
end
figure(3)
pt3=surf(x2,y2,tao1);%绘制滑靴底部的剪切压强场图
set(pt3,'edgecolor','none')
title('滑靴底部剪切压强场','FontSize',15,'FontWeight','bold','Color','r')
xlabel('r/mm','FontSize',15,'FontWeight','bold')
ylabel('r/mm','FontSize',15,'FontWeight','bold')
zlabel('压强/pa','FontSize',15,'FontWeight','bold')
colorbar
colormap("jet")
view(-40,40)%绘制滑靴底部速度场
r3=linspace(0,10,a2);
t3=linspace(0,360,b2);
x3=zeros(a2,b2);
y3=zeros(a2,b2);
for i=1:a2y3(i,:)=t3;
end
for j=1:b2x3(:,j)=r3;
end
figure(4)
pt4=surf(x3,y3,vrr1);%绘制滑靴底部的速度场图
set(pt4,'edgecolor','none')
title('滑靴底部速度场','FontSize',15,'FontWeight','bold','Color','r')
xlabel('h/um','FontSize',15,'FontWeight','bold')
ylabel('度','FontSize',15,'FontWeight','bold')
zlabel('速度m/s','FontSize',15,'FontWeight','bold')
colorbar
colormap("jet")
view(-40,40)

输出结果：
迭代次数为：422
迭代精度为：9.7821e-07
程序计算时间为：0.432
输出的主要参数为：
平均压强值为：17413903.2105
切应力平均值为：107590.4704
摩擦系数为：0.0061784
泄漏量为：0.00037913
泄漏量能量损失：791.6251
粘性摩擦功为：190.2184
总能量损失为：981.8435
密封面静压力为：656.4887
总静压力为：1096.3022
在这里插入图片描述在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

这篇关于通过雷诺方程运用matlab求解滑靴底部油膜厚度场、压力场、剪切场及速度场的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/625658。

相关文章

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【通俗理解】嵌入（Embedding）方程——自然语言处理的数学灵魂 关键词提炼 #嵌入方程 #自然语言处理 #词向量 #机器学习 #神经网络 #向量空间模型 #Siri #Google翻译 #AlexNet 第一节：嵌入方程的类比与核心概念【尽可能通俗】 嵌入方程可以被看作是自然语言处理中的“翻译机”，它将文本中的单词或短语转换成计算机能够理解的数学形式，即向量。 正如翻译机将一种语言
阅读更多...
poj 2431 poj 3253 优先队列的运用

poj 2431 poj 3253 优先队列的运用

poj 2431： 题意： 一条路起点为0， 终点为l。 卡车初始时在0点，并且有p升油，假设油箱无限大。 给n个加油站，每个加油站距离终点 l 距离为 x[i]，可以加的油量为fuel[i]。 问最少加几次油可以到达终点，若不能到达，输出-1。 解析： 《挑战程序设计竞赛》： “在卡车开往终点的途中，只有在加油站才可以加油。但是，如果认为“在到达加油站i时，就获得了一
阅读更多...
matlab读取NC文件（含group）

matlab读取NC文件（含group）

matlab读取NC文件（含group）： NC文件数据结构： 代码： % 打开 NetCDF 文件filename = 'your_file.nc'; % 替换为你的文件名% 使用 netcdf.open 函数打开文件ncid = netcdf.open(filename, 'NC_NOWRITE');% 查看文件中的组% 假设我们想读取名为 "group1" 的组groupName
阅读更多...
利用matlab bar函数绘制较为复杂的柱状图，并在图中进行适当标注

利用matlab bar函数绘制较为复杂的柱状图，并在图中进行适当标注

示例代码和结果如下：小疑问：如何自动选择合适的坐标位置对柱状图的数值大小进行标注？😂 clear; close all;x = 1:3;aa=[28.6321521955954 26.2453660695847 21.69102348512086.93747104431360 6.25442246899816 3.342835958564245.51365061796319 4.87
阅读更多...
C# double[] 和Matlab数组MWArray[]转换

C# double[] 和Matlab数组MWArray[]转换

C# double[] 转换成MWArray[], 直接赋值就行             MWNumericArray[] ma = new MWNumericArray[4];             double[] dT = new double[] { 0 };             double[] dT1 = new double[] { 0,2 };
阅读更多...
libsvm在matlab中的使用方法

libsvm在matlab中的使用方法

原文地址：libsvm在matlab中的使用方法 作者： lwenqu_8lbsk 前段时间，gyp326曾在论坛里问libsvm如何在matlab中使用，我还奇怪，认为libsvm是C的程序，应该不能。没想到今天又有人问道，难道matlab真的能运行libsvm。我到官方网站看了下，原来，真的提供了matlab的使用接口。 接口下载在： http://www.csie.ntu.edu.
阅读更多...
使用WebP解决网站加载速度问题，这些细节你需要了解

使用WebP解决网站加载速度问题，这些细节你需要了解

说到网页的图片格式，大家最常想到的可能是JPEG、PNG，毕竟这些老牌格式陪伴我们这么多年。然而，近几年，有一个格式悄悄崭露头角，那就是WebP。很多人可能听说过，但到底它好在哪？你的网站或者项目是不是也应该用WebP呢？别着急，今天咱们就来好好聊聊WebP这个图片格式的前世今生，以及它值不值得你花时间去用。 为什么会有WebP？ 你有没有遇到过这样的情况？网页加载特别慢，尤其是那
阅读更多...
Matlab/Simulink中PMSM模型的反电动势系数和转矩系数

Matlab/Simulink中PMSM模型的反电动势系数和转矩系数

Matlab/Simulink中PMSM模型的反电动势系数和转矩系数_matlab pmsm-CSDN博客
阅读更多...
MATLAB层次聚类分析法

MATLAB层次聚类分析法

转自：http://blog.163.com/lxg_1123@126/blog/static/74841406201022774051963/ 层次聚类是基于距离的聚类方法，MATLAB中通过pdist、linkage、dendrogram、cluster等函数来完成。层次聚类的过程可以分这么几步： (1) 确定对象（实际上就是数据集中的每个数据点）之间的相似性，实际上就是定义一个表征
阅读更多...
2024 年高教社杯全国大学生数学建模竞赛题目——2024 年高教社杯全国大学生数学建模竞赛题目的求解

2024 年高教社杯全国大学生数学建模竞赛题目——2024 年高教社杯全国大学生数学建模竞赛题目的求解

2024 年高教社杯全国大学生数学建模竞赛题目 （请先阅读“ 全国大学生数学建模竞赛论文格式规范 ”） 2024 年高教社杯全国大学生数学建模竞赛题目 随着城市化进程的加快、机动车的快速普及， 以及人们活动范围的不断扩大，城市道 路交通拥堵问题日渐严重，即使在一些非中心城市，道路交通拥堵问题也成为影响地方经 济发展和百姓幸福感的一个“痛点”，是相关部门的棘手难题之一。 考虑一个拥有知名景区
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2