本文主要是介绍牛客题霸 -- 【模板】完全背包,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!













参考代码:
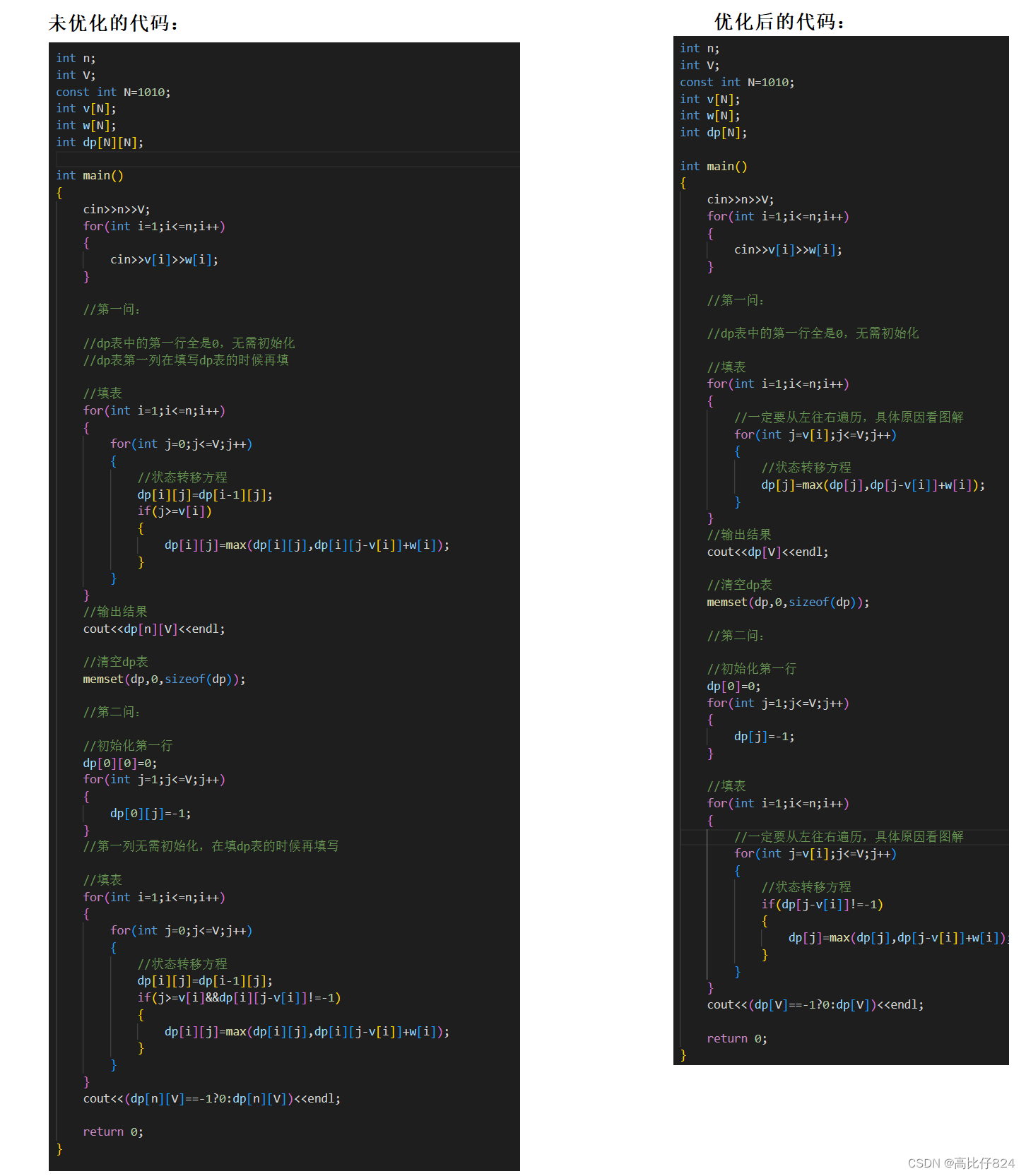
未优化的代码:
int n;
int V;
const int N=1010;
int v[N];
int w[N];
int dp[N][N];int main()
{cin>>n>>V;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}//第一问://dp表中的第一行全是0,无需初始化//dp表第一列在填写dp表的时候再填//填表for(int i=1;i<=n;i++){for(int j=0;j<=V;j++){//状态转移方程dp[i][j]=dp[i-1][j];if(j>=v[i]){dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);}}}//输出结果cout<<dp[n][V]<<endl;//清空dp表memset(dp,0,sizeof(dp));//第二问://初始化第一行dp[0][0]=0;for(int j=1;j<=V;j++){dp[0][j]=-1;}//第一列无需初始化,在填dp表的时候再填写//填表for(int i=1;i<=n;i++){for(int j=0;j<=V;j++){//状态转移方程dp[i][j]=dp[i-1][j];if(j>=v[i]&&dp[i][j-v[i]]!=-1){dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);}}}cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;return 0;
}
优化后的代码:
int n;
int V;
const int N=1010;
int v[N];
int w[N];
int dp[N];int main()
{cin>>n>>V;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}//第一问://dp表中的第一行全是0,无需初始化//填表for(int i=1;i<=n;i++){//一定要从左往右遍历,具体原因看图解for(int j=v[i];j<=V;j++){//状态转移方程dp[j]=max(dp[j],dp[j-v[i]]+w[i]);}}//输出结果cout<<dp[V]<<endl;//清空dp表memset(dp,0,sizeof(dp));//第二问://初始化第一行dp[0]=0;for(int j=1;j<=V;j++){dp[j]=-1;}//填表for(int i=1;i<=n;i++){//一定要从左往右遍历,具体原因看图解for(int j=v[i];j<=V;j++){//状态转移方程if(dp[j-v[i]]!=-1){dp[j]=max(dp[j],dp[j-v[i]]+w[i]);}}}cout<<(dp[V]==-1?0:dp[V])<<endl;return 0;
}
你学会了吗???
这篇关于牛客题霸 -- 【模板】完全背包的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






