本文主要是介绍Python数据分析案例37——基于分位数神经网络(QRNN)的汇率预测,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
案例背景
我导师的研究方向是少有的做"分位数回归"方向,作为研究机器学习深度学习方向的我自然就继承了这个特色,改进出了很多特殊结合方法,我会结合各种机器学习方法和各种分位数回归的方法。
之前写过分位数随机森林,分位数XGboost,分位数Lightgbm的文章:
Xgboost和Lightgbm结合分位数回归(机器学习与传统统计学结合)
本次带来一个小案例,分位数神经网络,神经网络是最简单的MLP架构,也就是很多外行论文里面所说的BP神经网络,结合分位数回归,就变成了'QRNN'。
数据介绍
本次做的是汇率的预测,即使用这样一个数据集:“汇率 外汇储备 M2 美国CPI 国债利率 贸易顺差”。用后面五个变量预测汇率。
需要本次案例演示的数据和全部代码的同学可以参考:汇率数据
方法流程
一般我不会写这个版块的,一般都是跟着代码走,但是由于这次做的模型较为复杂,不仅是QRNN模型,更是涉及到分位数的参数,不同的分位水平,然后进行不同
条件分布下的X对y的参数估计,形成了一个分布,然后再根据这个数据分布,进行包含留一交叉验证选择的带宽,再根据这个最优带宽进行核密度估计。然后再将核密度估计转化为不同情况下的(众数,中位数,均值)点估计。然后再去和真实值做对比,计算误差评价指标。(区间估计就不弄了,没必要....)
这个流程对于一般的同学来说复杂了,虽然对我来说只是一个研究之余随便搞点代码写的小案例....但很多不了解这些技术和方法的同学肯定看不懂。因为一般的同学做预测都是点估计,机器学习估计出来的都是一个点,一个具体数值,他们不懂啥是概率密度估计。我不打算介绍我这些东西的原理,因为大部分做这个方面的论文里面都有,我自己都是看论文学的(当然都是SCI论文),真的想研究的同学应该是明白我在做什么的,可以借鉴我这个小案例,然后推广到更多的数据和方法上。
简而言之就是基于QRNN模型做的概率密度估计。
并且我还会使用线性回归,线性分位数回归,普通神经网络,分位数神经网络去做一个预测误差的对比。
代码实现
开始写代码!导入包:
import os ,io
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=Falseimport tensorflow as tf
import keras
from keras.models import Model, Sequential
from keras.models import Sequential
from keras.layers import LSTM, Dense,Flatten
from keras.callbacks import EarlyStopping
from sklearn.preprocessing import MinMaxScaler
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
#from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_errorfrom sklearn.neighbors import KernelDensity
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import LeaveOneOut定义随机数种子,固定所有的包里面的随机数种子。
def set_my_seed():os.environ['PYTHONHASHSEED'] = '0'np.random.seed(1)tf.random.set_seed(66)
set_my_seed()准备数据
读取数据,设置日期为时间索引:
data=pd.read_csv('data.csv',parse_dates=['date'],index_col='date',encoding='utf-8')
data.index =data.index.to_period('M')
data.head()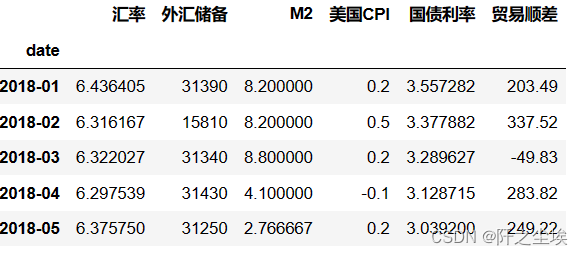
手工划分训练集和测试集
X=data.iloc[:,1:] ; y=np.log(data.iloc[:,0])
X_train=X[:'2023-05'] ; X_test=X['2023-06':]
y_train=y[:'2023-05'] ; y_test=y['2023-06':]
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)
只留下6个点作为测试集。小案例嘛,数据量不多,只是演示方法。
归一化,神经网络太需要归一化了
#归一化
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
##准备储存的数据框
df_preds_all=pd.DataFrame(index=y_test.index)
df_preds_all['真实值']=y_test
df_preds_all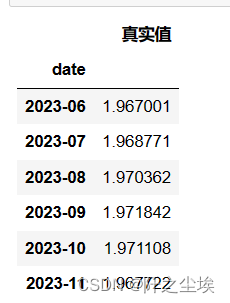
由于我要做很多模型对比,我要把不同模型的预测效果储存起来,就弄一个数据框准备好。
线性回归
#线性回归
from sklearn.linear_model import LinearRegression
linear_model = LinearRegression()
linear_model.fit(X_train, y_train)
y_pred_linear = linear_model.predict(X_test)
df_preds_all['线性回归预测']=y_pred_linear线性回归很简单,训练储存就行。
BP神经网络
#bp神经网络回归
bp_nn_model = MLPRegressor(hidden_layer_sizes=(20,18), activation='relu', solver='adam', max_iter=1000, random_state=0)
bp_nn_model.fit(X_train_scaled, y_train)
y_pred_bpnn = bp_nn_model.predict(X_test_scaled)
df_preds_all['BP网络预测']=y_pred_bpnn
df_preds_all 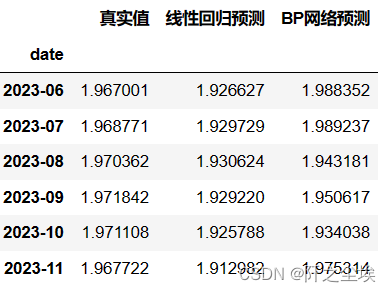
外行论文都喜欢叫BP神经网络。。其实就是最普通的多层感知机,MLP架构的神经网络,sklearn库就能实现,也很简单,训练拟合然后预测就行。
分位数回归
下面进行线性的分位数回归:
#分位数
from statsmodels.regression.quantile_regression import QuantReg
quantiles = np.around(np.linspace(0, 1, 51), decimals=2)[1:-1]
predictions = []for q in quantiles:model_quantile = QuantReg(y_train,X_train_scaled).fit(q=q)pred = model_quantile.predict(X_test_scaled)predictions.append(pred)prediction_QR = pd.DataFrame(predictions,index=[r'$\tau$='+str(i) for i in quantiles],columns=df_preds_all.index).T
prediction_QR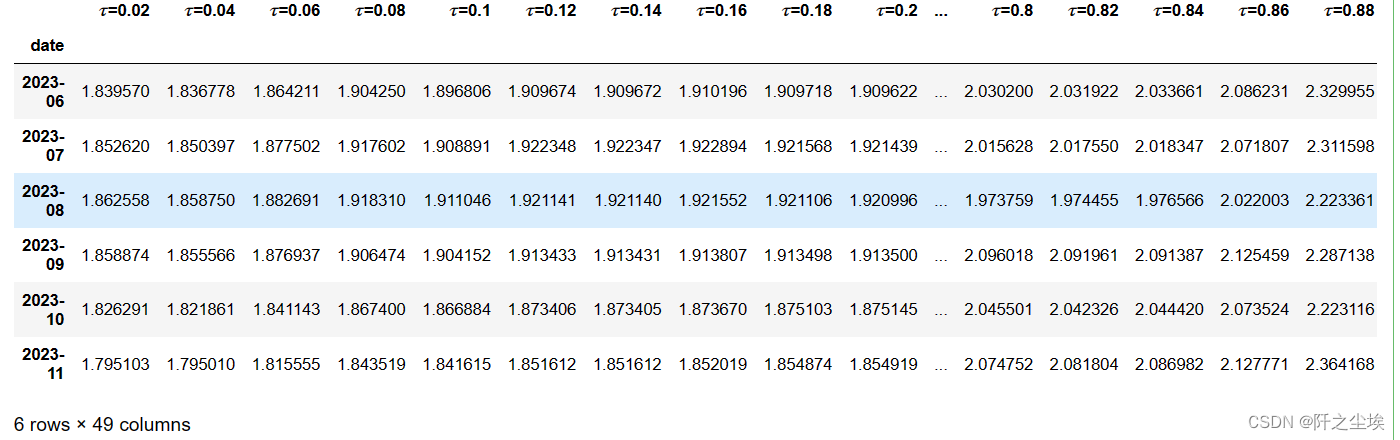
不同的分位数水平下的预测结果,我这里取的是间隔为0.02一个点的,也可以取0.05或者0.01,都可以,看你自己。
然后估计出来的是很多值嘛,我们需要做留一交叉验证的概率密度估计,然后构造为点估计:
df_alltau=prediction_QR.copy()
df_alltau_kde=pd.DataFrame()
set_my_seed()
bandwidths_lis=[]
for col in df_alltau.columns:X1=df_alltau[col].to_numpy().reshape(-1,1)grid = GridSearchCV(KernelDensity(kernel='gaussian'),{'bandwidth': np.linspace(0.01,0.2,21)},cv=LeaveOneOut())grid.fit(X1)best_KDEbandwidth = grid.best_params_['bandwidth']#print(best_KDEbandwidth)bandwidths_lis.append(best_KDEbandwidth)kde = KernelDensity(kernel="gaussian", bandwidth=best_KDEbandwidth).fit(X1)truth_density=pd.DataFrame(kde.score_samples(X1),columns=[col],index=df_alltau.index)df_alltau_kde=pd.concat([df_alltau_kde,truth_density],axis=1)
df_alltau_kde=np.exp(df_alltau_kde)row_sums = df_alltau_kde.sum(axis=1)
df_alltau_kde_s = df_alltau_kde.div(row_sums, axis=0)
df_eval_point_QR=pd.DataFrame(columns=['众数','中位数','均值'])
for col in df_alltau_kde_s.T.columns:pros=df_alltau_kde_s.T[col].to_numpy()values=df_alltau.T[col].to_numpy()#print(pros.shape,values.shape)max_values=values[np.argmax(pros)]median_values=np.median(values)mean_values=(pros*values).sum()df_eval_point_QR.loc[col,:]=[max_values,median_values,mean_values]
df_eval_point_QR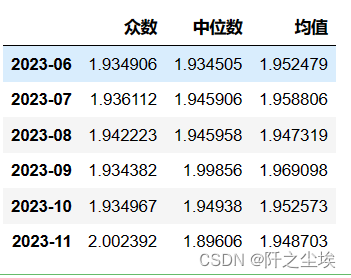
这就是普通的线性分位数回归的预测的三种情况的预测值了。
分位数神经网络QRNN
这里使用Keras框架,听说Keras现在也支持pytorch了。
def QRNN(X_train,hidden_dim=[64,32],tau=0.5):model = Sequential()model.add(Dense(hidden_dim[0],input_shape=(X_train_scaled.shape[1],)))model.add(Dense(hidden_dim[1]))model.add(Dense(1))set_my_seed()def loss_func(y_true, y_pred): loss_01 = tf.constant(tau,dtype=tf.float32)loss_02 = tf.constant(1-tau,dtype=tf.float32)loss_ = (tf.reduce_sum(tf.where(tf.greater(y_true, y_pred),(abs(y_true-y_pred))*loss_01,(abs(y_true-y_pred))*loss_02)))/y_train.shape[0] return loss_ model.compile(optimizer='Adam', loss=loss_func ,metrics=[tf.keras.metrics.RootMeanSquaredError(),"mape","mae"])return model分位数神经网络最大的区别在于损失函数,其实也是线性分位数回归和线性回归的最大区别。他们损失函数不一样而已。这里自定义了分位数的损失函数,然后传入,若只想借鉴QRNN代码,不想搞什么概率密度估计的同学看这个就可以了。
不同分位数水平下的预测:
predictions =np.zeros((quantiles.shape[0],y_test.shape[0]))
for i,q in enumerate(quantiles):set_my_seed()model=QRNN(X_train,hidden_dim=[9,7],tau=q)earlystop = EarlyStopping(monitor='loss', min_delta=0, patience=5)hist=model.fit(X_train_scaled,y_train,batch_size=4,epochs=50,callbacks=[earlystop],verbose=0)y_pred_QRNN = model.predict(X_test_scaled)predictions[i,:]=y_pred_QRNN.reshape(-1,)
prediction_QRNN = pd.DataFrame(predictions,index=[r'$\tau$='+str(i) for i in quantiles],columns=prediction_QR.index).T
prediction_QRNN 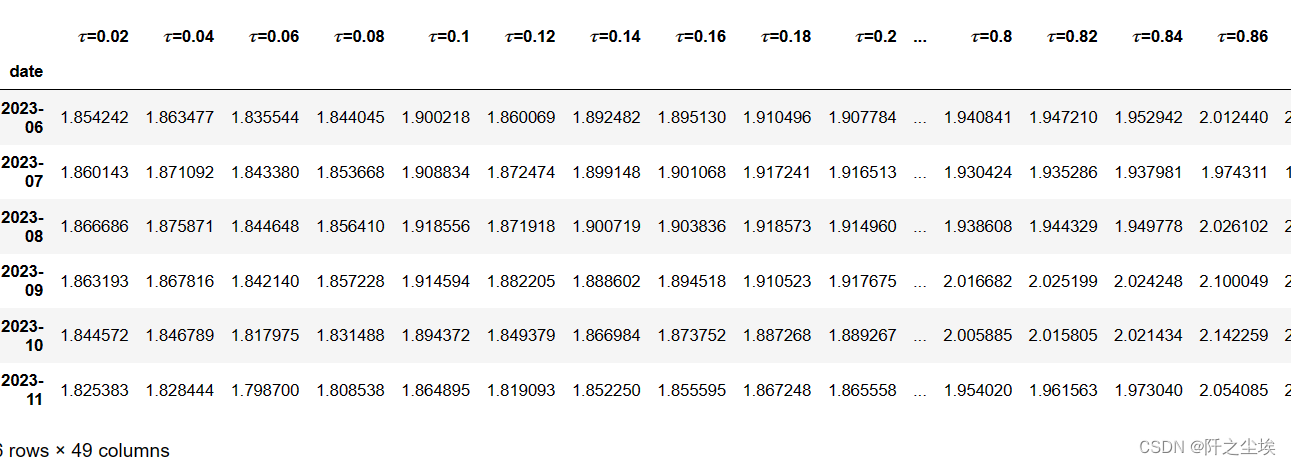
一样,使用留一交叉验证的概率密度估计
#构建为概率密度估计
df_alltau=prediction_QRNN.copy()
df_alltau_kde=pd.DataFrame()
set_my_seed()
bandwidths_lis=[]
for col in df_alltau.columns:X1=df_alltau[col].to_numpy().reshape(-1,1)grid = GridSearchCV(KernelDensity(kernel='gaussian'),{'bandwidth': np.linspace(0.01,0.2,21)},cv=LeaveOneOut())grid.fit(X1)best_KDEbandwidth = grid.best_params_['bandwidth']#print(best_KDEbandwidth)bandwidths_lis.append(best_KDEbandwidth)kde = KernelDensity(kernel="gaussian", bandwidth=best_KDEbandwidth).fit(X1)truth_density=pd.DataFrame(kde.score_samples(X1),columns=[col],index=df_alltau.index)df_alltau_kde=pd.concat([df_alltau_kde,truth_density],axis=1)
df_alltau_kde=np.exp(df_alltau_kde)
df_alltau_kde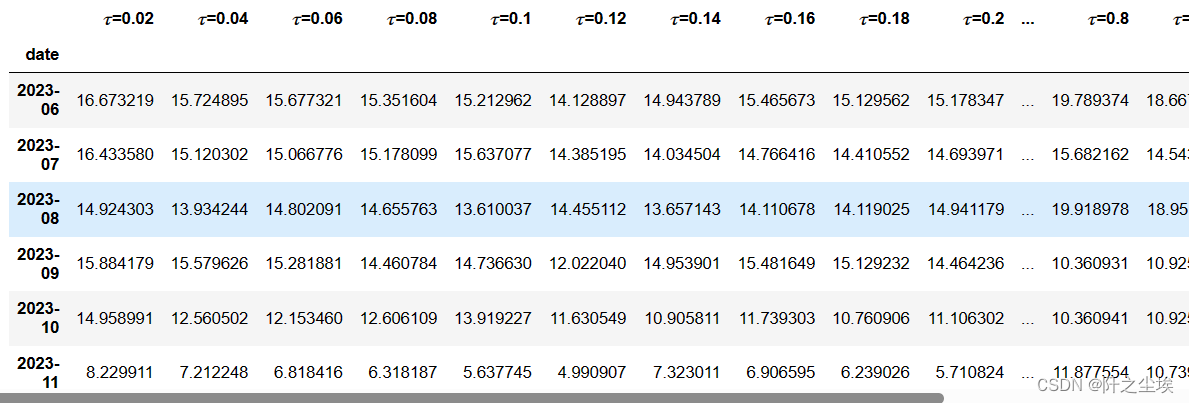
这里就是不同分位数水平下的概率密度,画图看就知道了:
dis_cols = 3 #一行几个
dis_rows = 2
off=0
plt.figure(figsize=(2.8 * dis_cols, 2.8 * dis_rows),dpi=400)
for i in range((dis_cols*dis_rows)):plt.subplot(dis_rows,dis_cols,i+1)sns.kdeplot(df_alltau.iloc[i,:],bw_adjust=0.3,fill=True,alpha=0.2,common_norm=True,label='预测值')plt.axvline(y_test[i+off],color='r',linestyle='--',label='真实值')plt.title(f'{df_alltau_kde.index[i+off]}',fontsize=14)plt.xlabel('汇率/对数',fontsize=10)plt.ylabel('条件密度',fontsize=10)plt.legend()
plt.tight_layout()
#plt.savefig('概率密度.png')
plt.show()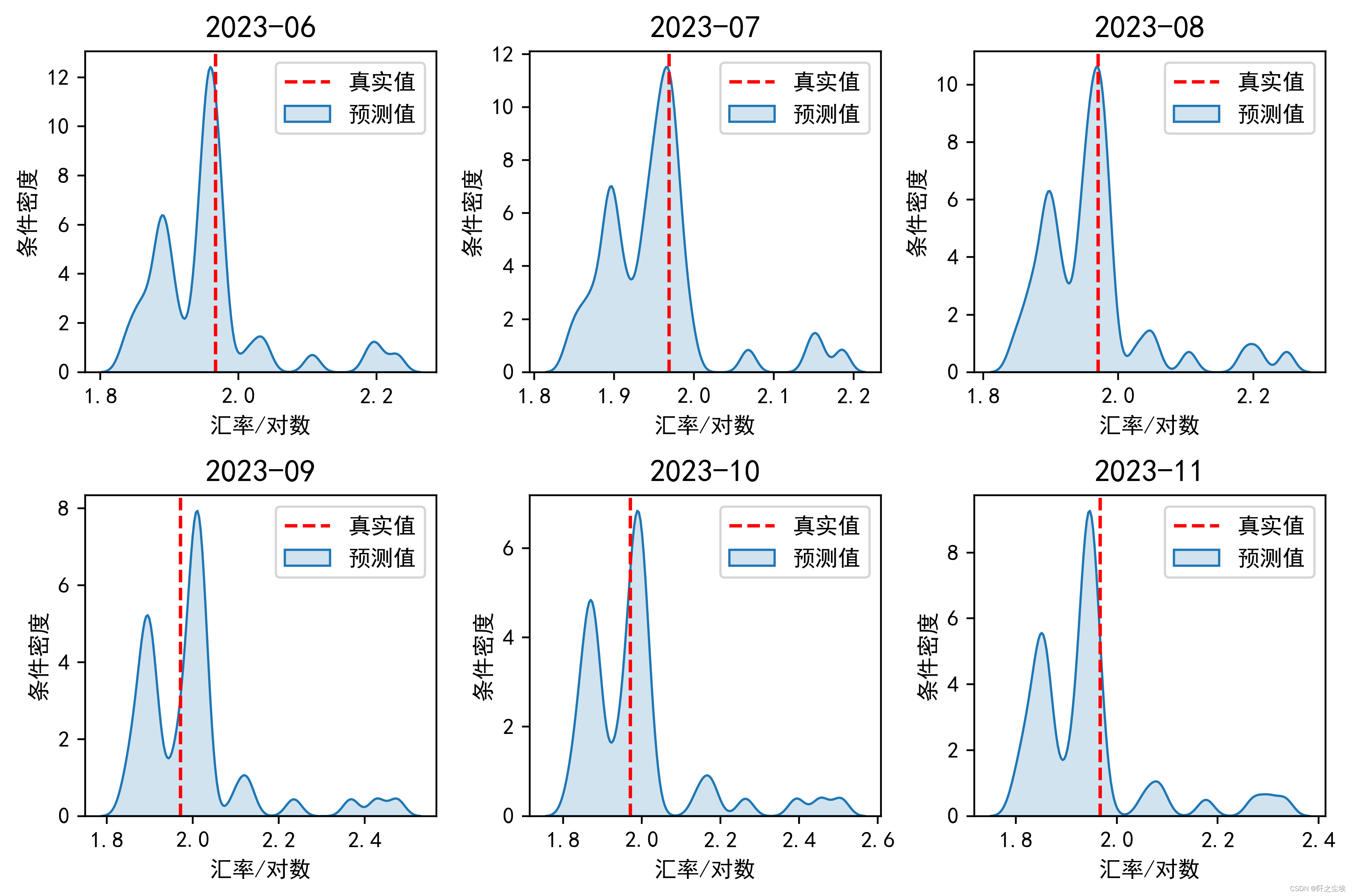
这图已经很明显了,我们的概率密度预测的峰值附近基本都是真实值,大概就是这样意思。
转为点估计
### 转为点估计
row_sums = df_alltau_kde.sum(axis=1)
df_alltau_kde_s = df_alltau_kde.div(row_sums, axis=0)
df_eval_point=pd.DataFrame(columns=['众数','中位数','均值'])
for col in df_alltau_kde_s.T.columns:pros=df_alltau_kde_s.T[col].to_numpy()values=df_alltau.T[col].to_numpy()#print(pros.shape,values.shape)max_values=values[np.argmax(pros)]median_values=np.median(values)mean_values=(pros*values).sum()df_eval_point.loc[col,:]=[max_values,median_values,mean_values]
df_eval_point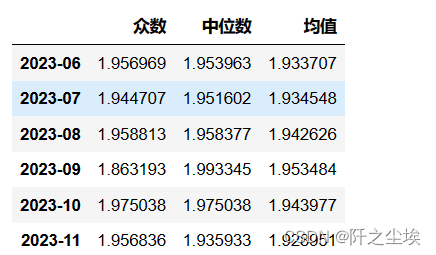
评价指标
基本都预测完了,现在就是把预测结果放一起然后进行评价了,构建一个多层索引,这样数据一目了然
tuples_li=[('真实值','真实值'),('线性回归', '预测值'), ('BP神经网络', '预测值')]
tuples_qr = [('分位数回归', '众数预测值'), ('分位数回归', '中位数预测值'), ('分位数回归', '均值预测值')]
tuples_qrnn = [('分位数神经网络', '众数预测值'), ('分位数神经网络', '中位数预测值'), ('分位数神经网络', '均值预测值')]
multi_index_li=pd.MultiIndex.from_tuples(tuples_li, names=['Model', 'Statistic'])
multi_index_qr = pd.MultiIndex.from_tuples(tuples_qr, names=['Model', 'Statistic'])
multi_index_qrnn = pd.MultiIndex.from_tuples(tuples_qrnn, names=['Model', 'Statistic'])df_preds_all.columns=multi_index_li
df_eval_point_QR.columns = multi_index_qr
df_eval_point.columns = multi_index_qrnndf_alls= pd.concat([df_preds_all,df_eval_point_QR, df_eval_point], axis=1)
df_alls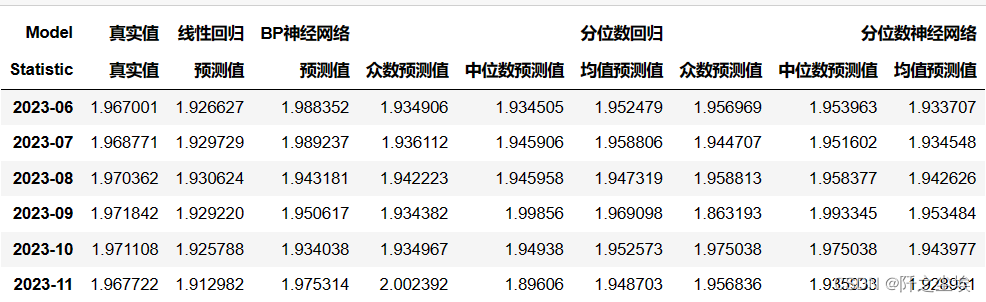
计算误差:
for col in df_alls.columns:if any('预测值' in part for part in col):error_percentage = (df_alls[col] - df_alls[('真实值', '真实值')]) / df_alls[('真实值', '真实值')] new_col_name = (col[0], f'{col[1]}误差')df_alls.insert( df_alls.columns.get_loc(col) + 1, new_col_name, error_percentage)
df_alls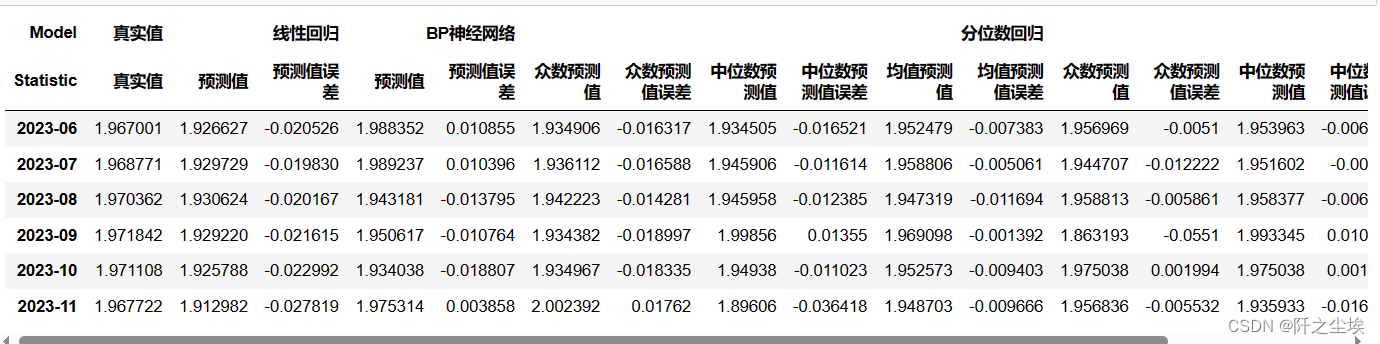
这种表就可以进论文了,存为excel复制一下进word就可以。
df_alls.to_excel('结果.xlsx')来看看某gpt对这个结果怎么分析的:
这段数据展示了对美元兑人民币汇率的不同模型预测,包括线性回归、BP神经网络、分位数回归和分位数神经网络,每个模型都给出了从2023年6月至11月的预测值及其误差。这些预测值是对汇率对数的估计,可以从中洞察到预测模型对未来汇率走势的看法。
预测误差的解读:
- 所有模型在大部分月份的预测值都略低于实际值,表示模型普遍预测人民币相对于美元将会有更强的表现。
- 然而,实际的汇率并没有像模型预测的那样表现出强势,这可能意味着存在一些未被模型考虑的因素或市场动态。
模型比较:
- 线性回归和BP神经网络在大多数情况下的预测误差较为接近,这可能表明在这个特定的预测任务中,简单的线性模型和更复杂的神经网络模型有相似的表现。
- 分位数回归和分位数神经网络在一些月份的预测误差较大,特别是在对极端值的预测上可能不够准确。
汇率走势分析:
- 预测结果普遍偏低,可能反映了模型对人民币强势的一种乐观预期。这种乐观可能基于对中国经济的正面评估或其他国际货币政策的预期。
- 但是人民币实际走势的表现不如模型的训练数据那样强势,可能是受到了这段时间国内外经济压力、政策和市场情绪的多重影响。
误差画图
一堆字,其实我自己都懒得看。。。把误差拿来画个图就知道那种模型预测效果好了:
df_alls.loc[:, df_alls.columns.get_level_values(1).str.contains("误差")]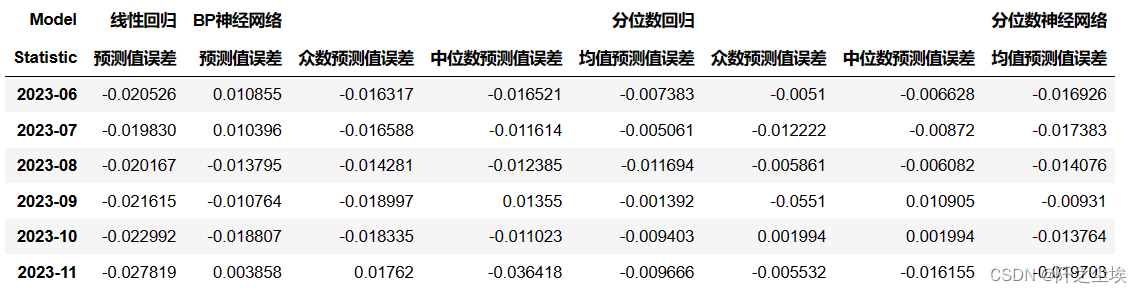
df=df_alls.loc[:, df_alls.columns.get_level_values(1).str.contains("误差")].abs().sum()
df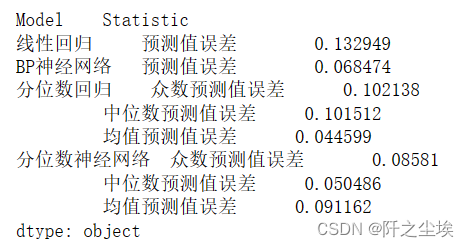
把这个数据拿出来画柱状图:
methods = ["线性回归", "BP神经网络", "分位数回归 众数", "分位数回归 中位数", "分位数神经网络 众数", "分位数神经网络 中位数"]
values = [0.132949, 0.068474, 0.102138, 0.101512, 0.08581, 0.050486]
#"分位数回归 均值", , "分位数神经网络 均值" 0.044599 , 0.091162
plt.figure(figsize=(7, 3),dpi=128)
sns.barplot(x=methods, y=values)
plt.xticks(rotation=35)
plt.ylabel("误差百分比")
plt.title("不同模型误差总和")
plt.show() 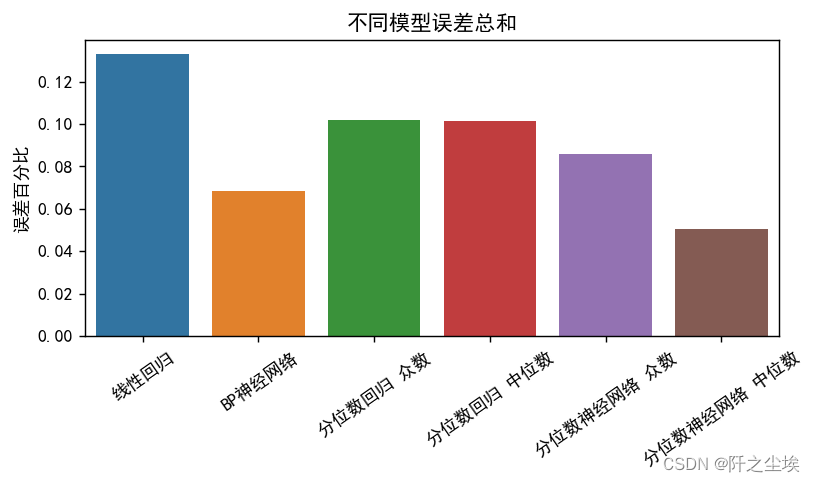
这就一目了然了,明显神经网络的效果会好,误差会低一点,
1.相比线性回归模型,无论普通线性回归还是分位数线性回归,都不如非线性的神经网络的误差低。
2.带分位数的模型,效果普遍比普通的模型效果好,分位数神经网络的中位数构建的点估计效果是最好的。
创作不易,看官觉得写得还不错的话点个关注和赞吧,本人会持续更新python数据分析领域的代码文章~(需要定制类似的代码可私信)
这篇关于Python数据分析案例37——基于分位数神经网络(QRNN)的汇率预测的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





