BFS，二分，并查集综合应用，P2658 汽车拉力比赛；P3958 [NOIP2017 提高组] 奶酪

题目描述

博艾市将要举行一场汽车拉力比赛。

赛场凹凸不平，所以被描述为M*N的网格来表示海拔高度(1≤ M,N ≤500)，每个单元格的海拔范围在0到10^9之间。

其中一些单元格被定义为路标。组织者希望给整个路线指定一个难度系数D，这样参赛选手从任一路标到达别的路标所经过的路径上相邻单元格的海拔高度差不会大于D。也就是说这个难度系数D指的是保证所有路标相互可达的最小值。任一单元格和其东西南北四个方向上的单元格都是相邻的。

输入格式

第一行两个整数M和N。第2行到第M+1行，每行N个整数描述海拔高度。第2+M行到第1+2M

行，每行N个整数，每个数非0即1，1表示该单元格是一个路标。

输出格式

一个整数，即赛道的难度系数D。

输入输出样例

输入 #1复制

3 5 
20 21 18 99 5  
19 22 20 16 26
18 17 40 60 80
1 0 0 0 1
0 0 0 0 0
0 0 0 0 1

输出 #1复制

21

题目所求的最大海拔差的最小值D满足：任意大于等于D的值也满足路标相互可达，只不过D是这些值中最小的哪个，满足单调性，所以可以考虑用二分来逼近D；

又因为需要判断“路标相互可达”，所以考虑用并查集来判断；

遍历地图优先考虑bfs

代码如下

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<map>
#include<set>
#include<stack>
#include<queue>
#include<cstdio>
#include<iomanip>using namespace std;
typedef long long LL;
const int N = 505;
int arr[N][N],arr1[N][N],fa[N*N],vis[N][N];
int n, m;
vector<pair<int, int>>p;
int ay[] = { 0,1,0,-1 }, ax[] = { 1,0,-1,0 };int find(int a) {if (fa[a] == a)return a;return fa[a] = find(fa[a]);
}void merge(int a, int b) {int x = find(a);int y = find(b);fa[x] = y;
}
void bfs(int D) {//这里的bfs不同于我们平时用队列写的bfs，这里的bfs更好写for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {for (int k = 0; k < 4; k++) {int ty = i + ay[k], tx = j + ax[k];if (ty <= 0 || tx <= 0 || ty > n || tx > m)continue;if (abs(arr[ty][tx] - arr[i][j]) > D)continue;merge((ty - 1) * m + tx, (i - 1) * m + j);}}}
}int check(int D) {for (int i = 1; i <= n * m; i++) {fa[i] = i;}bfs(D);int t = find((p[0].first - 1) * m + p[0].second);for (int i = 0; i < p.size(); i++) {if (find((p[i].first - 1) * m + p[i].second) != t)return 1;}return 0;
}int main() {scanf("%d%d", &n, &m);int mx = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {scanf("%d", &arr[i][j]);mx = max(mx, arr[i][j]);}}for (int i = 1; i <= n; i++) {for (int j = 1,t; j <= m; j++) {scanf("%d", &t);if (t == 1) {p.push_back({ i,j });}}}int l = 0, r = mx, mid, ans = 0;while (r >= l) {mid = l + (r - l) / 2;if (check(mid)) {l = mid + 1;}else {ans = mid;r = mid - 1;}}cout << ans << endl;return 0;
}

                        P3958 [NOIP2017 提高组] 奶酪

（这道题没有二分）

题目描述

现有一块大奶酪，它的高度为 ℎh，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为 z=0，奶酪的上表面为 z=h。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑 到奶酪的上表面去?

输入格式

每个输入文件包含多组数据。

第一行，包含一个正整数 T，代表该输入文件中所含的数据组数。

接下来是 T 组数据，每组数据的格式如下： 第一行包含三个正整数 n,h,r，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。

接下来的 n 行，每行包含三个整数 x,y,z，两个数之间以一个空格分开，表示空洞球心坐标为 (x,y,z)。

输出格式

T 行，分别对应 T 组数据的答案，如果在第 i 组数据中，Jerry 能从下表面跑到上表面，则输出 Yes，如果不能，则输出 No。

输入输出样例

输入 #1复制

3 
2 4 1 
0 0 1 
0 0 3 
2 5 1 
0 0 1 
0 0 4 
2 5 2 
0 0 2 
2 0 4

输出 #1复制

Yes
No
Yes

说明/提示

【输入输出样例 11 说明】

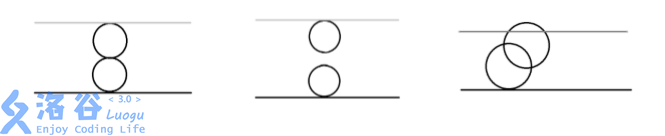
第一组数据,由奶酪的剖面图可见：

第一个空洞在 (0,0,0)(0,0,0) 与下表面相切；

第二个空洞在 (0,0,4)(0,0,4) 与上表面相切；

两个空洞在 (0,0,2)(0,0,2) 相切。

输出 Yes。

第二组数据,由奶酪的剖面图可见：

两个空洞既不相交也不相切。

输出 No。

第三组数据,由奶酪的剖面图可见：

两个空洞相交，且与上下表面相切或相交。

输出 Yes。

【数据规模与约定】

对于 20%20% 的数据，�=1n=1，1≤ℎ1≤h，�≤104r≤104，坐标的绝对值不超过 104104。

对于 40%40% 的数据，1≤�≤81≤n≤8，1≤ℎ1≤h，�≤104r≤104，坐标的绝对值不超过 104104。

对于 80%80% 的数据，1≤�≤1031≤n≤103，1≤ℎ,�≤1041≤h,r≤104，坐标的绝对值不超过 104104。

对于 100%100% 的数据，1≤�≤1×1031≤n≤1×103，1≤ℎ,�≤1091≤h,r≤109，�≤20T≤20，坐标的绝对值不超过 109109。

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
#include<map>
#include<set>
#include<stack>
#include<queue>using namespace std;
typedef long long LL;
const int N = 1e3 + 5;
typedef struct st {LL z, y, x;
}st;
st arr[N];
int fa[N];
int n, h;
LL r;int cmp(const st& a, const st& b) {if (a.z == b.z && a.y == b.y) {return a.x < b.x;}if (a.z == b.z) {return a.y < b.y;}return a.z < b.z;
}
int check(int target, int mid) {LL t = 2 * r;if ((arr[target].x - arr[mid].x) * (arr[target].x - arr[mid].x) + (arr[target].y - arr[mid].y) * (arr[target].y - arr[mid].y) > t * t)return 0;LL d = (arr[target].x - arr[mid].x) * (arr[target].x - arr[mid].x) + (arr[target].y - arr[mid].y) * (arr[target].y - arr[mid].y) + (arr[target].z - arr[mid].z) * (arr[target].z - arr[mid].z);if (d > t * t)return 0;return 1;
}
int find(int a) {if (fa[a] == a)return a;return fa[a] = find(fa[a]);
}void merge(int a, int b) {int x = find(a);int y = find(b);fa[x] = y;
}void bfs() {for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {if (check(i, j))merge(i, j);}}
}int main() {int T;scanf("%d", &T);while (T--) {scanf("%d%d%lld", &n, &h, &r);for (int i = 1; i <= n; i++) {scanf("%lld%lld%lld", &arr[i].x, &arr[i].y, &arr[i].z);}sort(arr + 1, arr + 1 + n, cmp);if (arr[n].z + r < h || arr[1].z>r) {printf("No\n");continue;}for (int i = 1; i <= n; i++)fa[i] = i;bfs();LL f = 0;for (int i = 1; arr[i].z <=r && i <= n; i++) {for (int j = n; j > 0 && arr[j].z >=h-r; j--) {if (find(i) == find(j)) {f = 1;break;}}if (f == 1)break;}if (f == 1)printf("Yes\n");elseprintf("No\n");}return 0;}