使用格雷戈里公式求pi的近似值

问题背景：

• 输入一个精度e,使用格雷戈里公式计算pi的近似值。

• 格雷戈里公式：

  

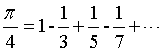
解决方案：

• 首先定义函数funpi(e)用来求pi的近似值。
• 使精确度精确到最后一项的绝对值小于e。
• 使用do-while循环控制是否需要持续输入。

程序源代码：

#include<stdio.h>
#include<math.h>
double funpi(double e);//函数声明
int main(void)
{char ch;double e,pi;do{printf("Enter e:");scanf("%lf",&e);pi=funpi(e);//调用函数printf("pi=%f\n",pi);printf("Do you want to continue?(Y/N):");scanf(" %c",&ch);} while((ch=='y')||(ch == 'Y'));printf("Thank you.\n");while(1);//显示return 0;
}double funpi(double e)//定义计算pi的函数
{int denominator,flag;double item,sum;flag=1;denominator=1;item=1.0;sum=0;while(fabs(item)>=e){item=flag*1.0/denominator;sum=sum+item;//累加flag=-flag;denominator=denominator+2;}return sum*4;
}

编译运行结果：

Enter e:0.001
pi=3.143589
Do you want to continue?(Y/N):Y
Enter e:0.0001
pi=3.141793
Do you want to continue?(Y/N):Y
Enter e:0.00001
pi=3.141613
Do you want to continue?(Y/N):n
Thank you.